决策树算法简介及其MATLAB、Pyhton实现

目录

决策树原理概述

决策树的经典算法：ID3算法

改进：C4.5算法

Hunt算法

决策树的优缺点

MATLAB实现决策树分类算法

基于python实现决策树

---

决策树原理概述

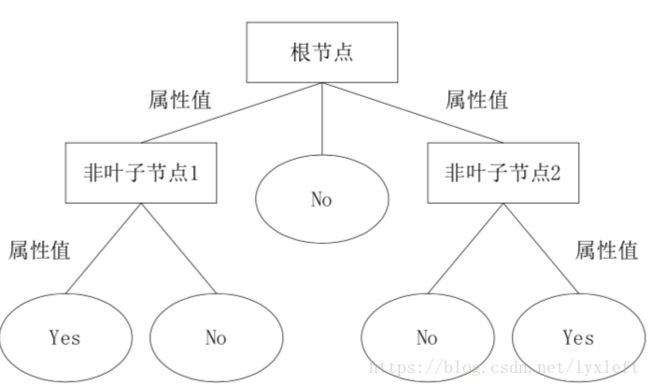
• 决策树通过把样本实例从根节点排列到某个叶子节点来对其进行分类。树上的每个非叶子节点代表对一个属性取值的测试， 其分支就代表测试的每个结果（yes no表示正类、负类）;而树上的每个叶子节点均代表一个分类的类别，树的最高层节点是根节点。当所有叶子节点给出的分类结果都一样时，就结束生长，即已经可以判定样本的类别。

• 根节点并没有什么实际的意义。

• 简单地说，决策树就是一个类似流程图的树形结构，采用自顶向下的递归方式，从树的根节点开始，在它的内部节点上进行属性值的测试比较，然后按照给定实例的属性值确定对应的分支，最后在决策树的叶子节点得到结论。这个过程在以新的节点为根的子树上重复。直到所有新节点给出的结果一致或足以判断分类（我们可以设计一些规则来决定）。

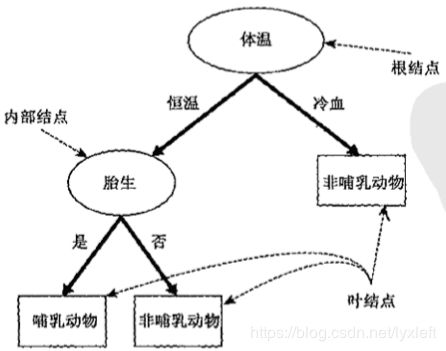
上图是一个区分动物类型的例子。

• 决策树其实很好理解。举个例子，它就像我们玩的猜谜底游戏。B向A提问，每次可以问不同的问题，而A只能回答是或不是，对或不对。通过多次发问，B越来越接近正确答案。这里，每个问题实际上就是非叶子节点的属性测试，是或者不是就是给出测试结果yes or no。如果一个谜底符合你所有问题（属性），得到答案一致，那么你一定能肯定这个谜底是什么。

• 分类树——面向离散变量的决策树；回归树——面向连续变量的决策树。

• 在决策树算法中，ID3 基于信息增益作为属性选择的度量，C4.5 基于信息增益比作为属性选择的 度量，CART 基于基尼指数作为属性选择的度量

• 优点：速度快、准确性高，便于理解。因为决策树的每个分支出来测试属性都是有实际的意义的，不像KNN之类直接用距离度量，没有实际的物理含义。决策树也适用于高维度的数据，不需要任何领域知识和参数假设。

• 缺点：对于各类别样本数量不一致的数据，信息增益偏向于那些具有更多数值的特征。容易过拟合。参见《模型过拟合及模型泛化误差评估》。

决策树的经典算法：ID3算法

原则上讲，对给定的数据集，可构造的决策树数目达到指数级。但是由于算力优先，我们只能在一定条件下构造出具有一定准确率的较优的决策树。这些算法通常都是采用贪心策略，在选择划分数据的属性时，采取一系列局部最优决策来构造决策树。

Hunt算法是许多决策树算法的基础，包括ID3、C4.5和CART。

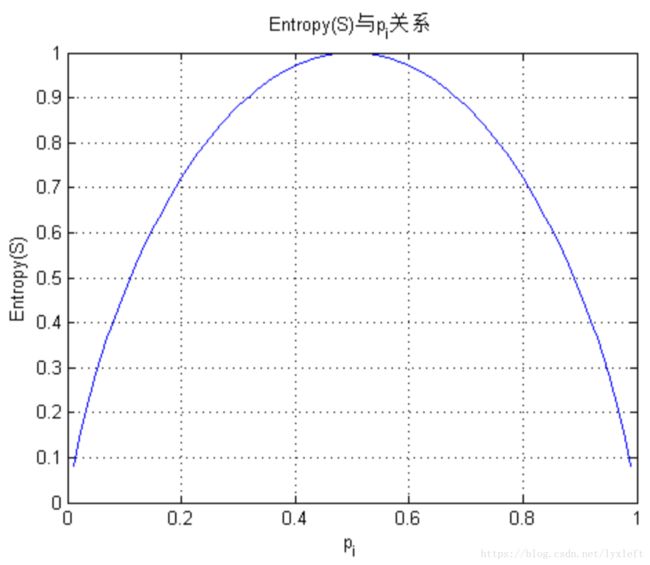
信息增益越大代表这个属性中包含的信息量越多。因为它的定义式实际上是熵的变化。

改进：C4.5算法

针对ID3算法中可能存在的问题，学者提出了一些改进。

针对上述两种算法，具体解释和举例可以参考：《数据挖掘系列（6）决策树分类算法》，此处不再赘述。

Hunt算法

在 Hunt 算法中，通过递归的方式建立决策树。
1)如果数据集 D 中所有的数据都属于一个类，那么将该节点标记为为节点。
2)如果数据集 D 中包含属于多个类的训练数据，那么选择一个属性将训练数据划分为较小的子集， 对于测试条件的每个输出，创建一个子女节点，并根据测试结果将 D 中的记录分布到子女节点中， 然后对每一个子女节点重复 1，2 过程，对子女的子女依然是递归的调用该算法，直至最后停止。

决策树的优缺点

优点：

–  决策树易于理解和实现。 人们在通过解释后都有能力去理解决策树所表达的意义。

–  对于决策树，数据的准备往往是简单或者是不必要的。其他的技术往往要求先把数据归一化，比如去掉多余的 或者空白的属性。

–  能够同时处理数据型和常规型属性。 其他的技术往往要求数据属性的单一。

–  是一个白盒模型。如果给定一个观察的模型，那么根据所产生的决策树很容易推出相应的逻辑表达式。

缺点：

– 对于各类别样本数量不一致的数据，在决策树当中信息增益的结果偏向于那些具有更多数值的特征。

– 决策树内部节点的判别具有明确性，这种明确性可能会带来误导。

MATLAB实现决策树分类算法

（数据：链接:https://pan.baidu.com/s/14WQOBF4oHJVtvX3V8WiJIQ  密码:5g22）

%% I. 清空环境变量
clear all
clc
warning off

%% II. 导入数据
load data.mat

%%
% 1. 随机产生训练集/测试集
a = randperm(569);
Train = data(a(1:500),:);
Test = data(a(501:end),:);

%%
% 2. 训练数据
P_train = Train(:,3:end);
T_train = Train(:,2);

%%
% 3. 测试数据
P_test = Test(:,3:end);
T_test = Test(:,2);

%% III. 创建决策树分类器
ctree = ClassificationTree.fit(P_train,T_train);

%%
% 1. 查看决策树视图
view(ctree);
view(ctree,'mode','graph');

%% IV. 仿真测试
T_sim = predict(ctree,P_test);

%% V. 结果分析
count_B = length(find(T_train == 1));
count_M = length(find(T_train == 2));
rate_B = count_B / 500;
rate_M = count_M / 500;
total_B = length(find(data(:,2) == 1));
total_M = length(find(data(:,2) == 2));
number_B = length(find(T_test == 1));
number_M = length(find(T_test == 2));
number_B_sim = length(find(T_sim == 1 & T_test == 1));
number_M_sim = length(find(T_sim == 2 & T_test == 2));
disp(['病例总数：' num2str(569)...
      '  良性：' num2str(total_B)...
      '  恶性：' num2str(total_M)]);
disp(['训练集病例总数：' num2str(500)...
      '  良性：' num2str(count_B)...
      '  恶性：' num2str(count_M)]);
disp(['测试集病例总数：' num2str(69)...
      '  良性：' num2str(number_B)...
      '  恶性：' num2str(number_M)]);
disp(['良性乳腺肿瘤确诊：' num2str(number_B_sim)...
      '  误诊：' num2str(number_B - number_B_sim)...
      '  确诊率p1=' num2str(number_B_sim/number_B*100) '%']);
disp(['恶性乳腺肿瘤确诊：' num2str(number_M_sim)...
      '  误诊：' num2str(number_M - number_M_sim)...
      '  确诊率p2=' num2str(number_M_sim/number_M*100) '%']);
  
%% VI. 叶子节点含有的最小样本数对决策树性能的影响
leafs = logspace(1,2,10);

N = numel(leafs);

err = zeros(N,1);
for n = 1:N
    t = ClassificationTree.fit(P_train,T_train,'crossval','on','minleaf',leafs(n));
    err(n) = kfoldLoss(t);
end
plot(leafs,err);
xlabel('叶子节点含有的最小样本数');
ylabel('交叉验证误差');
title('叶子节点含有的最小样本数对决策树性能的影响')

%% VII. 设置minleaf为13，产生优化决策树
OptimalTree = ClassificationTree.fit(P_train,T_train,'minleaf',13);
view(OptimalTree,'mode','graph')

%%
% 1. 计算优化后决策树的重采样误差和交叉验证误差
resubOpt = resubLoss(OptimalTree)
lossOpt = kfoldLoss(crossval(OptimalTree))

%%
% 2. 计算优化前决策树的重采样误差和交叉验证误差
resubDefault = resubLoss(ctree)
lossDefault = kfoldLoss(crossval(ctree))

%% VIII. 剪枝
[~,~,~,bestlevel] = cvLoss(ctree,'subtrees','all','treesize','min')
cptree = prune(ctree,'Level',bestlevel);
view(cptree,'mode','graph')

%%
% 1. 计算剪枝后决策树的重采样误差和交叉验证误差
resubPrune = resubLoss(cptree)
lossPrune = kfoldLoss(crossval(cptree))

基于python实现决策树

1）python实现熵计算：

def calcShannonEnt(dataSet): 
    numEntries = len(dataSet) 
    labelCounts = {}
    for featVec in dataSet:
        currentLabel = featVec[-1]
        if currentLabel not in labelCounts.keys():
            labelCounts[currentLabel] = 0
        labelCounts[currentLabel] += 1
    shannonEnt = 0.0
    for key in labelCounts:
        prob = float(labelCounts[key])/numEntries
        shannonEnt -= prob*log(prob,2) 
    return shannonEnt

2）SKlearn.tree介绍及使用建议：

官网:http://scikit-learn.org/stable/modules/generated/sklearn.tree.DecisionTreeClassifier.html

class sklearn.tree.DecisionTreeClassifier(criterion='gini', splitter='best', max_depth=None, min_samples_split=2,min_samples_leaf=1, max_f eatures=None, random_state=None, min_density=None, compute_importances=None,max_leaf_nodes=None)

重要参数：

criterion :规定了该决策树所采用的的最佳分割属性的判决方法，有两种:“gini”，“entropy”。

max_depth :限定了决策树的最大深度，对于防止过拟合非常有用。

min_samples_leaf :限定了叶子节点包含的最小样本数，这个属性对于防止上文讲到的数据碎片问 题很有作用

重要属性方法：

n_classes_ :决策树中的类数量。classes_ :返回决策树中的所有种类标签。
feature_importances_ :feature 的重要性，值越大那么越重要。
fit(X, y, sample_mask=None, X_argsorted=None, check_input=True, sample_weight=None)：将数据集 x，和标签集 y 送入分类器进行训练，这里要注意一个参数是:sample_weright，它和样本的数量一样长，所携带的是每个样本的权重。
get_params(deep=True)：得到决策树的各个参数。
set_params(**params)：调整决策树的各个参数。
predict(X)：送入样本 X，得到决策树的预测。可以同时送入多个样本。
transform(X, threshold=None)：返回 X 的较重要的一些 feature，相当于裁剪数据。
score(X, y, sample_weight=None)：返回在数据集 X,y 上的测试分数，正确率。

使用建议：

• 当我们数据中的 feature 较多时，一定要有足够的数据量来支撑我们的算法，不然的话很容易overfitting。（《降维和特征选择的关键方法介绍及MATLAB实现》）

• PCA是一种避免高维数据overfitting的办法。（《主成分分析（PCA）的线性代数推导过程》）

• 从一棵较小的树开始探索，用 export 方法打印出来看看。

• 善用 max_depth 参数，缓慢的增加并测试模型，找出最好的那个 depth。

• 善用 min_samples_split 和 min_samples_leaf 参数来控制叶子节点的样本数量，防止 overfitting。

• 平衡训练数据中的各个种类的数据，防止一个种类的数据 dominate。