【ML】GBDT/Adaboost算法原理-适用场景-优缺点-面试常问

一.简略介绍

GBDT（Gradient Boosting Decision Tree）又叫 MART（Multiple Additive Regression Tree），是一种迭代的决策树算法。GBDT主要由三个概念组成：Regression Decistion Tree（即DT)，Gradient Boosting（即GB)，Shrinkage (算法的一个重要演进分枝，目前大部分源码都按该版本实现）。搞定这三个概念后就能明白GBDT是如何工作的，要继续理解它如何用于搜索排序则需要额外理解RankNet概念，之后便功德圆满。sklearn中GBDT文档 scikit-learn地址。

1 .DT：回归树 Regression Decision Tree

GBDT 中的树全部都是回归树，核心就是累加所有树的结果作为最终结果。只有回归树的结果累加起来才是有意义的，分类的结果累加是没有意义的。

GBDT 调整之后可以用于分类问题，但是内部还是回归树。

这部分和决策树中的是一样的，无非就是特征选择。回归树用的是最小化均方误差，分类树是用的是最小化基尼指数（CART)

提起决策树（DT, Decision Tree) 绝大部分人首先想到的就是C4.5分类决策树。但如果一开始就把GBDT中的树想成分类树，那就是一条歪路走到黑，一路各种坑，最终摔得都要咯血了还是一头雾水说的就是LZ自己啊有木有。咳嗯，所以说千万不要以为GBDT是很多棵分类树。决策树分为两大类，回归树和分类树。前者用于预测实数值，如明天的温度、用户的年龄、网页的相关程度；后者用于分类标签值，如晴天/阴天/雾/雨、用户性别、网页是否是垃圾页面。这里要强调的是，前者的结果加减是有意义的，如10岁+5岁-3岁=12岁，后者则无意义，如男+男+女=到底是男是女？ GBDT的核心在于累加所有树的结果作为最终结果，就像前面对年龄的累加（-3是加负3），而分类树的结果显然是没办法累加的，所以GBDT中的树都是回归树，不是分类树，这点对理解GBDT相当重要（尽管GBDT调整后也可用于分类但不代表GBDT的树是分类树）。那么回归树是如何工作的呢？

2.GB：梯度迭代 Gradient Boosting

从GradientDescend到GradientBoosting

首先 Boosting 是一种集成方法。通过对弱分类器的组合得到强分类器，他是串行的，几个弱分类器之间是依次训练的。GBDT 的核心就在于，每一颗树学习的是之前所有树结论和的残差。

Gradient 体现在：无论前面一颗树的 cost function 是什么，是均方差还是均差，只要它以误差作为衡量标准，那么残差向量都是它的全局最优方向，类似于求梯度，这就是 Gradient。

 

3. Shrinkage

Shrinkage（缩减）是 GBDT 算法的一个重要演进分支，目前大部分的源码都是基于这个版本的。

核心思想在于：Shrinkage 认为每次走一小步来逼近结果的效果，要比每次迈一大步很快逼近结果的方式更容易防止过拟合。

也就是说，它不信任每次学习到的残差，它认为每棵树只学习到了真理的一小部分，累加的时候只累加一小部分，通过多学习几棵树来弥补不足。每一步的残差计算其实变相的增大了分错样本的权重，而已经分对的样本则都趋向于 0。这样后面就更加专注于那些分错的样本。

没用Shrinkage时：（yi表示第i棵树上y的预测值， y(1~i)表示前i棵树y的综合预测值）

y(i+1) = 残差(y1~yi)， 其中： 残差(y1~yi) =  y真实值 - y(1 ~ i)

y(1 ~ i) = SUM(y1, ..., yi)

Shrinkage不改变第一个方程，只把第二个方程改为： 

y(1 ~ i) = y(1 ~ i-1) + step * yi

具体的做法就是：仍然以残差作为学习目标，但是对于残差学习出来的结果，只累加一小部分（step* 残差）逐步逼近目标，step 一般都比较小 0.01-0.001, 导致各个树的残差是渐变而不是陡变的。

本质上，Shrinkage 为每一颗树设置了一个 weight，累加时要乘以这个 weight，但和 Gradient 没有关系。

这个 weight 就是 step。跟 AdaBoost 一样，Shrinkage 能减少过拟合也是经验证明的，目前还没有理论证明。

具体的公式：

4.其他

算法的整体流程：

终止条件

• 树的节点数
• 树的深度
• 没有适合分割的节点

特征值排序

在对每个节点进行分割的时候，首先需要遍历所有的特征，然后对每个样本的特征的值进行枚举计算。（CART）
在对单个特征量进行枚举取值之前，我们可以先将该特征量的所有取值进行排序，然后再进行排序。
优点
避免计算重复的value值
方便更佳分割值的确定
减少信息的重复计算

多线程/MPI并行化的实现

通过MPI实现对GBDT的并行化，最主要的步骤是在建树的过程中，由于每个特征值计算最佳分割值是相互独立的，故可以对特征进行平分，再同时进行计算。

二.GBDT 适用场景

GBDT 可以适用于回归问题（线性和非线性）；

GBDT 也可用于二分类问题（设定阈值，大于为正，否则为负）和多分类问题。

三.GBDT的优缺点

GBDT主要的优点有：

　　　　1) 可以灵活处理各种类型的数据，包括连续值和离散值。

　　　　2) 在相对少的调参时间情况下，预测的准备率也可以比较高。这个是相对SVM来说的。

　　　　3）使用一些健壮的损失函数，对异常值的鲁棒性非常强。比如 Huber损失函数和Quantile损失函数。

               4) 很好的利用了弱分类器进行级联。

               5) 充分考虑的每个分类器的权重。

GBDT的主要缺点有：

　　　　1)由于弱学习器之间存在依赖关系，难以并行训练数据。不过可以通过自采样的SGBT来达到部分并行。
 

其他.面试常问GBDT相关

1. 怎么设置单棵树的停止生长条件？

设置参数：

• 节点分裂时的最小样本数；min_samples；
• 最大深度：max_depth；
• 最多叶子节点数：max_leaf_nodes；
• loss满足约束条件。

2. 如何评估特征的权重大小？

（1）计算每个特征在训练集下的特征增益，与所有特征的信息增益之和的比例为权重值。
（2）借鉴投票机制。用相同的参数对 w 每个特征训练一个模型，计算各模型下每个特征正确分类的个数，每个特征正确分类个数与所有正确分类个数之和的比例为权重值。

3. --当增加样本数量时，训练时长是线性增加的吗？

不是，因为生成单棵决策树时，需要选择最佳分裂点，以拟合残差，寻找最优的拟合值，而这个运算与样本个数N不是线性相关的。

4. --当增加树的颗数时，训练时长是线性增加的吗？

不是，因为每棵树生成的时间复杂度不同。
叶子节点数和每棵树的生成时间复杂度也不成正比。

5. 每个节点上保存什么信息？

树的中间节点保存某个特征的分割值，叶节点保存预测时某个类别的概率。

6.如何防止过拟合？

（1）增加样本，移除噪声；
（2）减少特征，保留重要的特征；
（3）对样本进行采样，建树的时候，选择一个子集（GBDT特有的方法，是无放回抽样）；每一个子树都采用这个样本子集进行拟合。

7. gbdt 在训练和预测的时候都用到了步长，这两个步长一样么？

（1）这两个步长一样么？答：训练跟预测时，两个步长是一样的，也就是预测时的步长为训练时的步长，从训练的过程可以得知（更新当前迭代模型的时候）。
（2）都有什么用，如果不一样，为什么？答：它的作用就是使得每次更新模型的时候，使得loss能够平稳地沿着负梯度的方向下降，不至于发生震荡。
（3）那么怎么设步长的大小?
答：有两种方法，一种就是按策略来决定步长，另一种就是在训练模型的同时，学习步长。
A. 策略：
a 每个树步长恒定且相等，一般设较小的值；
b 开始的时候给步长设一个较小值，随着迭代次数动态改变或者衰减。
B. 学习：
因为在训练第k棵树的时候，前k-1棵树时已知的，而且求梯度的时候是利用前k-1棵树来获得。所以这个时候，就可以把步长当作一个变量来学习。
（4）（太小？太大？）在预测时，对排序结果有什么影响？
答：如果步长过大，在训练的时候容易发生震荡，使得模型学不好，或者完全没有学好，从而导致模型精度不好。
而步长过小，导致训练时间过长，即迭代次数较大，从而生成较多的树，使得模型变得复杂，容易造成过拟合以及增加计算量。
不过步长较小的话，使训练比较稳定，总能找到一个稳定的局部最优解。
个人觉得过大过小的话，模型的预测值都会偏离真实情况（可能比较严重），从而导致模型精度不好。
（5）跟shrinking里面的步长一样么？答：这里的步长跟shrinking里面的步长是一致的。

8. gbdt中哪些部分可以并行？

A. 计算每个样本的负梯度
B. 分裂挑选最佳特征及其分割点时，对特征计算相应的误差及均值时
C. 更新每个样本的负梯度时
D. 最后预测过程中，每个样本将之前的所有树的结果累加的时候

 

GBDT 的调参

参数说明（sklearn）
n_estimators：控制弱学习器的数量
max_depth：设置树深度，深度越大可能过拟合
max_leaf_nodes：最大叶子节点数
learning_rate：更新过程中用到的收缩步长，(0, 1]
max_features：划分时考虑的最大特征数，如果特征数非常多，我们可以灵活使用其他取值来控制划分时考虑的最大特征数，以控制决策树的生成时间。
min_samples_split：内部节点再划分所需最小样本数，这个值限制了子树继续划分的条件，如果某节点的样本数少于min_samples_split，则不会继续再尝试选择最优特征来进行划分。
min_samples_leaf：叶子节点最少样本数，这个值限制了叶子节点最少的样本数，如果某叶子节点数目小于样本数，则会和兄弟节点一起被剪枝。
min_weight_fraction_leaf：叶子节点最小的样本权重和，这个值限制了叶子节点所有样本权重和的最小值，如果小于这个值，则会和兄弟节点一起被剪枝。
min_impurity_split：节点划分最小不纯度，使用 min_impurity_decrease 替代。
min_impurity_decrease：如果节点的纯度下降大于了这个阈值，则进行分裂。
subsample：采样比例，取值为(0, 1]，注意这里的子采样和随机森林不一样，随机森林使用的是放回抽样，而这里是不放回抽样。如果取值为1，则全部样本都使用，等于没有使用子采样。如果取值小于1，则只有一部分样本会去做 GBDT 的决策树拟合。选择小于1的比例可以减少方差，即防止过拟合，但是会增加样本拟合的偏差，因此取值不能太低，一般在 [0.5, 0.8] 之间。

 

CART回归树如何进行回归？

第一步是遍历特征和切分点，找到分裂后左右节点MSE最小(即分裂后混程度最低)的特征和切分点；
第二步以该特征和切分点进行分裂，计算输出值；
重复上述步骤，直至达到停止条件(混乱程度小于一定数值、树深达到要求)
生成决策树。

关于损失函数的选取

在回归问题中，LossFunction一般会选取MSE；而在二分类问题中，损失函数一般是LogLoss，在多分类问题上，损失函数则会是指数损失。

关于分类与回归的区别

1.分类和回归时，损失函数是不同的
2.回归时，第一棵树直接通过标签真实值来训练；而在分类时，需要将真实值进行sigmoid映射。
 

RF与GBDT之间的区别与联系？

1）相同点：

都是由多棵树组成

最终的结果都由多棵树共同决定。

2）不同点：

a 组成随机森林的树可以分类树也可以是回归树，而GBDT只由回归树组成

b 组成随机森林的树可以并行生成（Bagging）；GBDT 只能串行生成（Boosting）；这两种模型都用到了Bootstrap的思想。

c 随机森林的结果是多数表决表决的，而GBDT则是多棵树加权累加之和

d 随机森林对异常值不敏感，而GBDT对异常值比较敏感

e 随机森林是减少模型的方差，而GBDT是减少模型的偏差

f 随机森林不需要进行特征归一化。而GBDT则需要进行特征归一化

g随机森林对训练集一视同仁权值一样，GBDT是基于权值的弱分类器的集成 

xgboost/gbdt在调参时为什么树的深度很少就能达到很高的精度？

现象：xgboost/gbdt仅仅用梯度上升法就能用6个节点的深度达到很高的预测精度，DecisionTree/RandomForest的时候需要把树的深度调到15或更高。（xgb倾向于先解决50%的问题，在解决25%的问题，再解决10%的问题，慢慢逼近解）

答：Boosting主要关注降低偏差，因此Boosting能基于泛化性能相当弱的学习器构建出很强的集成；Bagging主要关注降低方差，因此它在不剪枝的决策树、神经网络等学习器上效用更为明显。

其实就机器学习算法来说，其泛化误差可以分解为两部分，偏差（bias)和方差(variance)。这个可由下图的式子导出（这里用到了概率论公式D(X)=E(X2)-[E(X)]2）。偏差指的是算法的期望预测与真实预测之间的偏差程度，反应了模型本身的拟合能力；方差度量了同等大小的训练集的变动导致学习性能的变化，刻画了数据扰动所导致的影响。这个有点儿绕，不过你一定知道过拟合。

如下图所示，当模型越复杂时，拟合的程度就越高，模型的训练偏差就越小。但此时如果换一组数据可能模型的变化就会很大，即模型的方差很大。所以模型过于复杂的时候会导致过拟合。

当模型越简单时，即使我们再换一组数据，最后得出的学习器和之前的学习器的差别就不那么大，模型的方差很小。还是因为模型简单，所以偏差会很大。

Adaboosting和gbdt的区别

GBDT不是Adaboost Decistion Tree。就像提到决策树大家会想起C4.5，提到boost多数人也会想到Adaboost。Adaboost是另一种boost方法，它按分类对错，分配不同的weight，计算cost function时使用这些weight，从而让“错分的样本权重越来越大，使它们更被重视”。Bootstrap也有类似思想，它在每一步迭代时不改变模型本身，也不计算残差，而是从N个instance训练集中按一定概率重新抽取N个instance出来（单个instance可以被重复sample），对着这N个新的instance再训练一轮。由于数据集变了迭代模型训练结果也不一样，而一个instance被前面分错的越厉害，它的概率就被设的越高，这样就能同样达到逐步关注被分错的instance，逐步完善的效果。Adaboost的方法被实践证明是一种很好的防止过拟合的方法，但至于为什么则至今没从理论上被证明。GBDT也可以在使用残差的同时引入Bootstrap re-sampling，GBDT多数实现版本中也增加的这个选项，但是否一定使用则有不同看法。re-sampling一个缺点是它的随机性，即同样的数据集合训练两遍结果是不一样的，也就是模型不可稳定复现，这对评估是很大挑战，比如很难说一个模型变好是因为你选用了更好的feature，还是由于这次sample的随机因素。

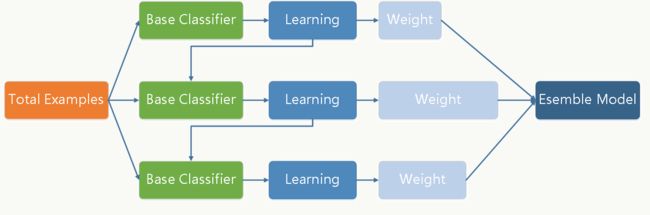
Adaboosting算法流程：

 

参考链接：

1.主讲gbdt原理：https://blog.csdn.net/qq_19446965/article/details/82079624?depth_1-utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-1&utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-1

2.参数空间和函数空间区别：https://www.jianshu.com/p/6075922a8bc3

3.gbdt的一些介绍：https://blog.csdn.net/qq_19446965/article/details/82079624

4.雪伦的介绍：https://blog.csdn.net/a819825294/article/details/51188740

5.https://blog.csdn.net/Daverain/article/details/96702696