数据结构之线性表【C语言】

数据结构之线性表【C语言】

参考书籍：大话数据结构

举个“栗子”

今天我们介绍数据结构中最常用和最简单的一种结构，在介绍它之前先讲个例子。

假如我有个儿子，我经常下午去幼儿园接送儿子，每次都能在门口石到老师带着小朋友们，一个拉着另一个的衣服，依次从教室出来。而且我发现很有规律的是，每次他们的次序都是一样。比如我儿子排在第5 个，每次他都是在第5 个，前面同样是那个小女孩，后面一直是那个小男孩。这点让我很奇怪，为什么一定要这样？

有一天我就问老师原因。她告诉我，为了保护小朋友的安全，避免漏掉小朋友，所以给他们安排了出门的次序，不先规定好了，谁在谁的前面，谁在谁的后面。这样养成习惯后，如果有谁没有到位，他前面和后面的小朋友就会主动报告老师，某人不在。即使以后如果要外出到公园或博物馆等情况下，老师也可以很快地清点人数，万一有人走丢，也能在最快时间知道，及时去寻找。

我一想，还真是这样。小朋友们始终按照次序排队做事，出意外的情况就可能会少很多。毕竟，遵守秩序是文明的标志，应该从娃娃抓起。而且，真要有人丢失，小孩子反而是最认真负责的监督员。

再看看门外的这帮家长们，都挤在大门口，哪个分得清他们谁是谁呀。与小孩子们的井然有序形成了鲜明的对比。哎，有时大人的所作所为，其实还不如孩子。这种排好队的组织方式，其实就是今天我们要介绍的数据结构线性表．

线性表的定义

线性表，从名字上你就能感觉到，是具有像线一样的性质的表。在广场上，有很多入分散在各处，当中有些是小朋友，可也有很多大人，甚至还有不少宠物，这些小朋友的数据对于整个广场人群来说，不能算是线性表的结构。但像刚才提到的那样，一个班级的小朋友，有一个打头，有一个收尾，当中的小朋友每一个都知道他前面一个是谁，他后面一个是准，这样如同有一根线把他们串联起来了。就可以称之为线性表。

这里需要强调几个关键的地方。

• 首先它是一个序列． 也就是说，元素之间是有顺序的，若元素存在多个，则第一个元素无前驱，最后一个元素无后继，其他每个元素都有且只有一个前驱和后继。如果一个小朋友去拉两个小朋友后面的衣服，那就不可以排成一队了，同样，如果一个小朋友后面的衣服，被两个甚至多个小朋友拉扯，这其实是在打架，而不是有序排队．
• 然后，线性表强调是有限的，小朋友班级人数是有限的， 元素个数当然也是有限的。事实上，在计算机中处理的对象都是有限的，那种无限的数列，只存在于数学的概念中。
• 元素的类型要是同一类型的

线性表元素的个数n (n > O ) 定义为线性表的长度，当n=O 时，称为空表。

在非空表中的每个数据元素都有一个确定的位置，如a ， 是第一个数据元素， an 足最后一个数据元素， ai 是第l 个数据元素，称i 为数据元素a i 在线性表中的位序。

线性表的抽象数据类型

前面我们巳经给了线性表的定义，现在我们来分析一下，线性表应该有一些什么样的操作呢？

还是回到刚才幼儿园小朋友的例子，老师为了让小朋友有秩序地出入， 所以就为虑给他们排一个队，并且是长期使用的顺序，这个考虑和安排的过程其实就是一个线性表的创建和初始化过程．

一开始没经验，把小朋友排好队后，发现有的高有的矮， 于是就让小朋友解散重新排~是一个线性表重置为空表的操作．

排好了队，我们随时可以叫出队伍某一位置的小朋友名字及他的具体情况． 比如有家长问，队伍里第五个孩子， 怎么这么调皮，他叫什么名字呀，老师可以很快告诉这位家长，这就是封清扬的儿子，叫封云卞． 我在旁就非常扭捏，石来是我给儿子的名字没取好，儿子让班级．风云突变．了． 这种可以根据位序得到数据元素也是一种
很重要的线性表操作．

还有什么呢，有时我们想知道，某个小朋友， 比如麦兜是否是班里的小朋友，老师会告诉我说，不是，麦兜在春田花花幼儿园里，不在我们幼儿园。这种查找某个元素是否存在的操作很常用．

而后有家长问老师，班里现在到底有多少个小朋友呀，这种获得线性表长度的问题也很普遍。

显然，对于一个幼儿园来说，加入一个新的小朋友到队列中，或因某个小朋友生病，需要移除某个位置，都是很正常的情况．对于一个线性表来说，插人数据和删除数据都是必须的操作．

所以，线性表的抽象数据类型定义如下

ADT 线性表
Data
		线性表的数据对象集合为（a1，a2，...., an）每个元素的类型均为DataType。其中，除第一个元素a1外，每个元素有且仅有一个直接前驱元素，除了最后一个元素an外，每个元素都有且仅有一个直接后继元素。数据元素之间的关系是一对一的关系
Operation（基本的线性表操作）：
		InitList (*L);  初始化操纵，建立一个空的线性表L
		ListEmpty(L);  若线性表为空，返回true，否则返回false
		ClearList(*L); 将线性表清空
		GetElem(L,i,*e)：将线性表L中的第i个位置的元素值返回给e
		LocateElem(L,e): 在线性表L中查找与给定值e相等的元素，如果查找成功，返回该元素在表中序号表示成功，否则返回0表示失败
		ListInsert(*L,i,e): 在线性表L中的第i个位置插入新元素e
		ListDelete(*L,i,*e): 删除线性表L中第i个位置元素，并用e返回其值
		ListLength(L): 返回线性表L的元素的个数

上面列出了线性表的基本操作下面会对各个操作一一实现的
对于不同的应用，线性表的基本操作是不同的， 上述操作是最基本的，对于实际问题中涉及的关于线性表的更复杂操作，完全可以用这些基本操作的组合来实现．

比如，要实现两个线性表集合A 和B 的并集操作． 即要使得集合A=A U B . 说白了，就是把存在焦合B 中但并不存在A 中的数据元素插入到A 中即可。

线性表的顺序存储结构

顺序结构的定义

说了那么多的线性表，我们来看看线性表的两种物理结构的第一种——顺序存储结构。

线性表的顺序存储结构，指的是用一段地址连续的存储单元一次存储的线性表的数据元素

示意表如下：

顺序表的存储方式

线性表的顺序存储结构，说白了，和刚才的例子一样，就是在内存中找了块地儿，通过占位的形式，把一定内存空间给占了，然后把相同数据类型的数据元素依次存放在这块空地中． 既然线性表的每个数据元素的类型都相同，所以可以用C 语言（其他语言也相同）的一维数组来实现顺序存储结构， 即把第一个数据元素存到数组下标为0 的位置中， 接右把线性表相邻的元素存储在数组中相邻的位置。建立一个线性表， 要在内存中找一块
地，于是这块地的第一个位置就非常关键， 它是存储空间的起始位置．

你可以把线性表的创建比作在图书馆占位置，这样的模型联系更加有助于你去理解线性表，占座时，如果图书馆里空座很多，你当然不必一定要选择第一排第一个位子，而是可以选择风水不错、美女较多的地儿。找到后，放一个书包在第一个位，就表示从这开始， 这地方暂时归我了。接若，因为我们一共九个人，所以我需要占九个座。线性表中，我们估算这个线性表的最大存储容贷，建立一个数组，数组的长度就是这个最大存储容员．

可现实中， 我们宿舍总有那么几个不是很好学的人， 为了游戏，为了恋爱， 就不去图书馆自习了。假设我们九个人，去了六个，真正被使用的座位也就只是六个， 另三个是空的。同样的，我们已经有了起始的位置，也有了最大的容忧， 于是我们可以在里面增加数据了。随行数据的插入， 我们线性表的长度开始变大，不过线性表的当前长度不能超过存储容优，即数组的长度。想想也是，如果我们有十个人，只占了九个座，自然是坐不下的。

这一段的例子是从大话数据结构这本书上引用的，我认为这种比喻方式非常的形象。将建立数组比作在大学图书馆占位置。

Code

#define MAXSIZE 20 // 存储空间初始分配量
typedef int ElemType // ElemType 类型根据实际情况而定，这里假设为int * / 
typedef struct{
	ElemType data[MAXSIZE]; // 数组存储的数据元素，最大值为MAXSIZE
	int length; // 线性表当前的长度
}SqList；

这里，我们就发现描述顺序存储结构需要三个属性

• 存储空间的起始位置: 数组data，它的存储位置就是存储空间的存储位置。
• 线性表的最大储存容量：数组长度MaxSize
• 线性表的当前长度length

数据长度和线性表长度区别

数组的长度是存放线性农的存储空间的长度，存储分配后这个员是一般是不变的。一般在级语言，比如C, VB 、C+ ＋都可以用编程手段实现动态分配数组，不过这会带来性能上的损耗。

线性表的长度是线性表中数据元素的个数，随着线性表插入和删除操作的进行，这个量是变化的。在任意时刻， 线性表的长度应该小于等于数组的长度。

地址计算方法

由于我们数数都是从1 开始数的，线性表的定义也不能免俗，起始也是1 , 可C语言中的数组却是从0 开始第一个下标的，于是线性表的第i 个元素是要存储在数组下标为，－ 1 的位置，即数据元素的序号和存放它的数组下标之间存在对应关系，如下图所示：

其实，内存中的地址，就和图书馆或电影院里的座位一样， 都是有编号的。存储器中的每个存储单元都有自己的编号，这个编号称为地址，由于每个数据元素，不管它是整型、实型还是字符型，它都是需要占用一定的存储单元空间的。假设占用的是C 个存储单元，那么线性表中第i +1 个数据元素的存储位置和第i 个数据元素的存储位置满足下列关系(LOC 表示获得存储位置的函数)
$$\mathrm{LOC}\left(a_{i+1}\right)=\mathrm{LOC}\left(a_i\right)+c$$
所以对于第i个数据元素ai的存储位置可以由a1推算出：
$$\mathrm{LOC}\left({\mathrm{a}}_i\right)=\mathrm{L}\mathrm{O}\mathrm{C}\left({\mathrm{a}}_1\right)+(\mathrm{i}-1)\ast \mathrm{c}$$

通过这个公式，你可以随时扛出线性表中任意位置的地址，不管它是第一个还是最后一个，都是相同的时间。那么我们对每个线性表位置的存人或者取出数据，对于计算机来说都是相等的时间，也就是一个常数，因此用我们绊法中学到的时间复杂度的概念来说，它的存取时间性能为0(1 ） 。我们通常把具有这一特点的存储结构称为随
机存取结构。

顺序结构的插入与删除

获取元素操作：

对于线性表的顺序存储结构来说，如果我们要实现GetElem操作， 即将线性表L中的第 i 个位置元素值返回，其实是非常简单的。就程序而官，只要 i 的数值在数组下标范围内，就是把数组第i -1 下标的值返回即可。来行代码

#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
typedef int Status;
// Status是函数类型，其值是函数结果状态代码，如OK等
// 初始条件：顺序线性表L已经存在， i <= i <= ListLength(L)
// 操作结果：用e返回 L中的第i个元素的值
Status GetElem(SqList L,int i,ElemType *e)
{
	if(L.length == 0 || i<1 || i>L.length)
		return ERROR;
	*e = L.data[i-1];
	return OK
}

插入操作

刚才我们也谈到，这里的时间复杂度为0(1) 。我们现在来考虑，如果我们要实现Listlnsert ( *L，i，e ), 即在线性表L 中的第i 个位置插人新元素e , 应该如何操作？

• 如果插入位置不合理，抛出异常
• 如果线性表长度大于数组长度，则抛出异常或动态容量增加
• 从最后一个元素开始向前遍历第i个位置，分别将它们都先后移动一个位置；
• 将要插入元素填在位置i处；

实现代码如下

//---insert into the SqList---
Status ListInsert(SqList *L,int i,ElemType e)
{
	int k;
	if(L->length == MAXSIZE) // SqList is full
		return ERROR;
	if(i<1 || i>L->length+1) // when i is not in the right range
		return ERROR;
	if(i<=L->length) // If the inserted content is not at the end of the list
	{
		for(k=L->length-1; k=i-1; k--)
		{
			L->data[k+1] = L->data[k];
		}
	}
	L->data[i-1] = e; // insert the new number
	L->length ++;
	return OK;
}

删除操作

删除算法的思路：

• 如果删除位置不合理，抛出异常
• 取出删除元素
• 从删除位置开始遍历到最后一个元素位置，分别将它们都先后移动一个位置
• 表长减一

Code

//---delete the number in the SqList---

Status ListDelete(SqList *L,int i,ElemType *e)
{
	int k;
	if(L->length==0) // SqList is empty
		return ERROR;
	if(i<1 || i>L->length) // the location of the delete is error
	{
		return ERROR;
	}
	*e = L->data[i-1];
	if (ilength)
	{
		for(k=i; klength; k++) // Moves the element forward after the deleted number's position
			L->data[k-1] = L->data[k];
	}
	L->length--;
	return OK;
}

线性表顺序存储结构的优缺点

线性表的链式存储结构

这里我们只讨论，动态链表的相关操作；

链表的创建和初始化

其实C 语言真是好东西，它具有的指针能力，使得它可以非常容易地操作内存中的地址和数据，这比其他高级语官更加灵活方便。后来的面向对象语言，如Java 、C#等，虽不使用指针，但因为启用了对象引用机制，从某种角度也间接实现了指针的某些作用。

对于链表的创建和初始化，其实就是对于头节点的创建，这个头节点是无论如何也不能丢失的,下面我们把他封装成一个函数

首先先简单的创建一个节点结构体

struct Node{
    int number;
    struct Node *next;
};

typedef struct Node Node;

接下来我们写一个createNode()的函数用来创建头节点，也是对链表的初始化

// create node
Node *createNode() {
    Node *node = (Node *) malloc(sizeof(Node));
    node->next = NULL;
    return node;
}

链表的插入操作

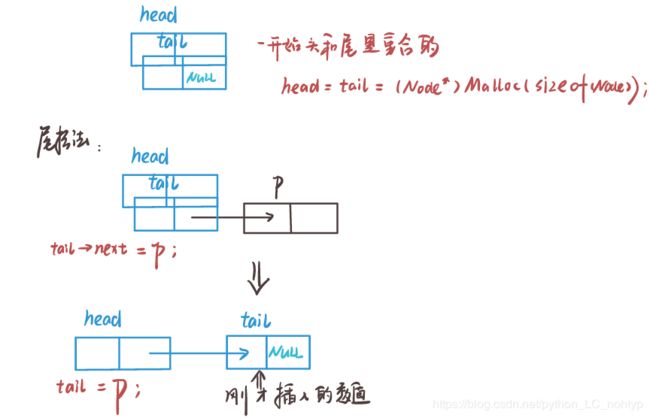
尾部插入

尾插的时候你需要先找到那个尾巴才行，也就是需要一个遍历的过程，我们也把他封装成一个函数

void tailInsert(Node *head, int number) {
    // init tail
    Node *tail = createNode();
    tail = head;
    // find the tail
    while (tail->next) {
        tail = tail->next;
    }
    // insert the number
    Node *temp = createNode();
    temp->next = NULL;
    temp->number = number;
    tail->next = temp;
}

这里我画了一个示意图可以参考一下：

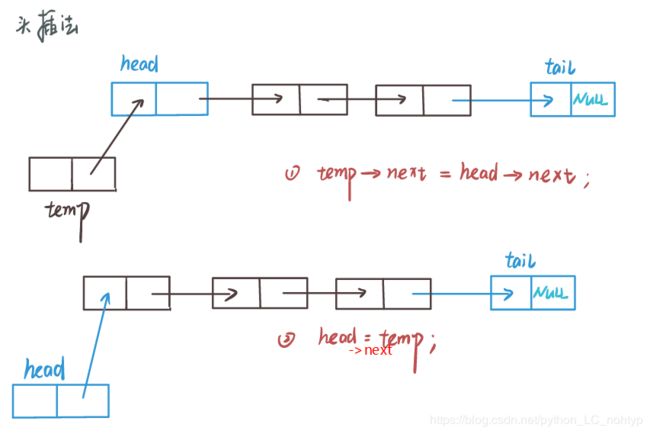
头部插入

头插法的特点就是从头部插入，同样的我们把它封装成一个函数。

Node *headInsert(Node *head,int number)
{
    Node *temp = createNode();
    temp->number = number;
    temp->next = head->next;
    head->next = temp;
    return head;
}

示意图：

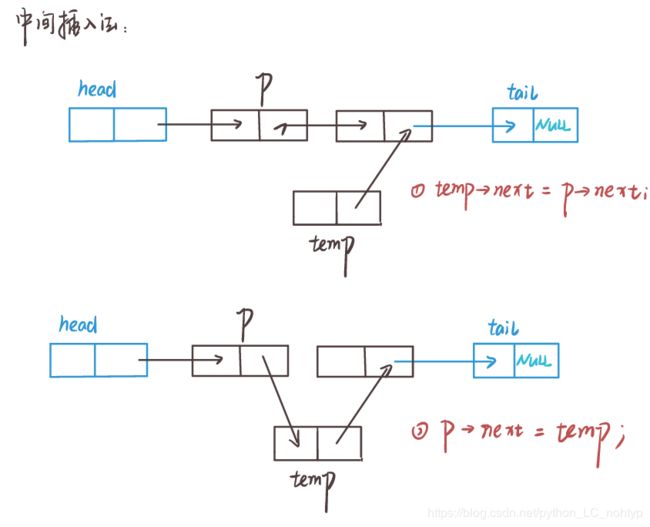
中间插入

我这里因为结构体设置的比较简单所以就是用number来作为插入的标志，在别的结构体当中你可以把它换成其他的

void middleInsert(Node *head, int num,int number)
{
    Node *p = createNode();
    for (p=head->next;p!=NULL;p=p->next) {
        if (p->number == num)
        {
            Node *temp = createNode();
            temp->number = number;
            temp->next = p->next;
            p->next = temp;
            break;
        }
    }
}

示意图：

链表的遍历操作

对于链表遍历的基本思想就是，看一看p->next的是不是NULL了，以这个作为一个标志。因为头节点我们是不可以动的，所以我们需要多一个指针指向头节点来代替头节点去完成这个遍历的操作，你可以把一般名为为p，tail也行

我们把这个操作也封装成一个函数

void traverseLink(Node *head)
{
    Node *p = createNode();
    p = head;
    for(p=head->next;p!=NULL;p=p->next)
    {
        printf("%d\n",p->number);
    }
}

链表的删除操作

想要删除链表中的一个元素很简单，就是让上一个元素的指针跳过中间那个直接指向下一个就ok啦。

void deleteNode(Node *head,int number)
{
    Node *p = createNode();
    for (p=head->next;p->next !=NULL;p=p->next) {
        if (p->next->number == number)
        {
            p->next = p->next->next;

        }
    }
}