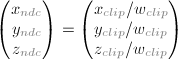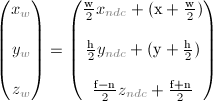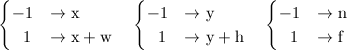详解MVP矩阵之ProjectionMatrix

简介

透视投影是3D固定流水线的重要组成部分，是将相机空间中的点从视锥体(frustum)变换到规则观察体(Canonical View Volume)中，待裁剪完毕后进行透视除法的行为。在算法中它是通过透视矩阵乘法和透视除法两步完成的。

 

具体的理论推导过程可以参考下面的几个Link，

深入探索透视投影变换

深入探索透视投影变换(续)

OpenGL Transformation

OpenGL ProjectionMatrix

推导正交投影变换

 

代码实现

 

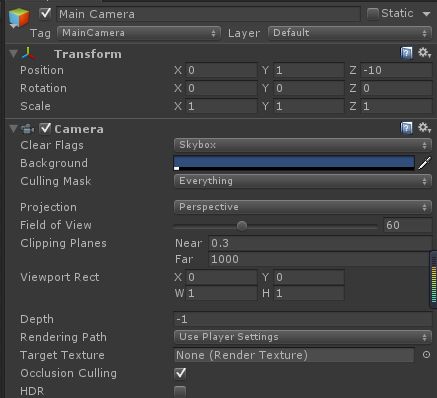
首先是Perspective的Camera，用Unity的Camera来作为参照。

 

 

(0,0,0)点放一个quad

加一个脚本来测试一下

 

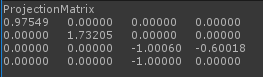
Debug.Log("ProjectionMatrix\n" + GetComponent().projectionMatrix);
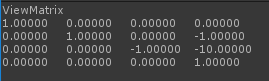
Debug.Log("ViewMatrix\n" + GetComponent().worldToCameraMatrix);
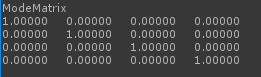
Debug.Log("ModeMatrix\n" + mesh.transform.localToWorldMatrix);

     

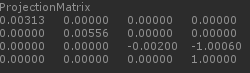
打印出相机的矩阵，结果如下

 

打印quad各个顶点的位置。

 

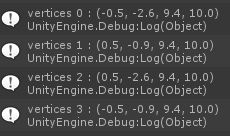
经过计算

P * V *M * Vector4(pos, 1) ,得到结果

 

C++ 代码

camera = new Camera(Vector3(0, 1, -10), 60,16.0f / 9, 0.3f, 1000);
    Matrix4x4 model = Matrix4x4::identity;
 
    qDebug() <<"ProjectionMatri: " << camera->GetProjectionMatrix();
    qDebug() << "ViewMatrix: " << camera->GetViewMatrix();
    qDebug() << "ModelMatrix: " << model;
 
    Vector3 vertice0(-0.5f, -0.5F, 0);
    Vector3 vertice1(0.5f, 0.5F, 0);
    Vector3 vertice2(0.5f, -0.5F, 0);
    Vector3 vertice3(-0.5f, 0.5F, 0);
 
    Matrix4x4 mvp = camera->GetProjectionMatrix() * camera->GetViewMatrix() * model;
    //Vector3 tmp = mvp * vertice0;
    qDebug() << "vertice0" << mvp * Vector4(vertice0.x, vertice0.y, vertice0.z, 1);
    qDebug() << "vertice1" << mvp * Vector4(vertice1.x, vertice1.y, vertice1.z, 1);
    qDebug() << "vertice2" << mvp * Vector4(vertice2.x, vertice2.y, vertice2.z, 1);
    qDebug() << "vertice3" << mvp * Vector4(vertice3.x, vertice3.y, vertice3.z, 1);
 

结果

 

其中

Perspective函数如下

Matrix4x4 Transform::Perspective(float fovy, float aspect, float zNear, float zFar)
{
   
    float tanHalfFovy = tan(Mathf::Deg2Rad * fovy / 2);
 
    Matrix4x4 result(0.0f);
    result[0 * 4 + 0] = 1.0f / (aspect * tanHalfFovy);
    result[1 * 4 + 1] = 1.0f / (tanHalfFovy);
    result[2 * 4 + 3] = -1.0f;
 
    result[2 * 4 + 2] = -(zFar + zNear) / (zFar - zNear);
    result[3 * 4 + 2] = -(2.0f * zFar * zNear) / (zFar - zNear);
    return result;
}
 

同样功能的还有Frustum函数

Matrix4x4 Transform::Frustum(float l, float r, float b, float t, float zNear, float zFar)
{
    Matrix4x4 result(0.0f);
 
    result[0] = 2 * zNear / (r - l);
    result[8] = (r + l) / (r - l);
    result[5] = 2 * zNear / (t - b);
    result[9] = (t + b) / (t - b);
    result[10] = -(zFar + zNear) / (zFar - zNear);
    result[14] = -(2 * zFar * zNear) / (zFar - zNear);
    result[11] = -1;
    result[15] = 0;
    return result;
}

 

Opengl的流水线如下图

乘完了MVP矩阵，得到的是Clip Coordinates。

坐标除以w之后（称为透视除法），得到了NDC坐标

 

最后通过线性变换，得到最终的屏幕空间坐标。

 

Opengl里面设置view port通常是这样

glViewport(x, y, w, h);
glDepthRange(n, f);

对应关系如下

 

还是继续上面的例子进行计算

 

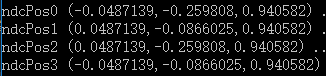
同除以w之后，得到NDC坐标

 
    Vector3 ndcPos0 = Vector3(clipPos0.x / clipPos0.w, clipPos0.y / clipPos0.w, clipPos0.z / clipPos0.w);
    Vector3 ndcPos1 = Vector3(clipPos1.x / clipPos1.w, clipPos1.y / clipPos1.w, clipPos1.z / clipPos1.w);
    Vector3 ndcPos2 = Vector3(clipPos2.x / clipPos2.w, clipPos2.y / clipPos2.w, clipPos2.z / clipPos2.w);
   Vector3 ndcPos3 = Vector3(clipPos3.x / clipPos3.w, clipPos3.y / clipPos3.w, clipPos3.z / clipPos3.w);

 

在一个640* 360 的窗口中，

    int x = 0, y = 0, w = 640, h = 360, n = 0.3, f =1000;
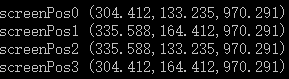
    Vector3 screenPos0(w * 0.5f * ndcPos0.x + x + w * 0.5f, h* 0.5f * ndcPos0.y + y + h *0.5f, 0.5f *(f - n) * ndcPos0.z + 0.5f * (f + n));
    Vector3 screenPos1(w * 0.5f * ndcPos1.x + x + w * 0.5f, h* 0.5f * ndcPos1.y + y + h *0.5f, 0.5f *(f - n) * ndcPos1.z + 0.5f * (f + n));
    Vector3 screenPos2(w * 0.5f * ndcPos2.x + x + w * 0.5f, h* 0.5f * ndcPos2.y + y + h *0.5f, 0.5f *(f - n) * ndcPos2.z + 0.5f * (f + n));
    Vector3 screenPos3(w * 0.5f * ndcPos3.x + x + w * 0.5f, h* 0.5f * ndcPos3.y + y + h *0.5f, 0.5f *(f - n) * ndcPos3.z + 0.5f * (f + n));

 

和最终显示的结果一致。

 

完整的代码

	//Perspective matrix test
/*
	camera = new Camera(Vector3(0, 1, -10), 60, 16.0f / 9, 0.3f, 1000);
	Matrix4x4 model = Matrix4x4::identity;

	qDebug() <<"ProjectionMatri: " << camera->GetProjectionMatrix();
	qDebug() << "ViewMatrix: " << camera->GetViewMatrix();
	qDebug() << "ModelMatrix: " << model;

	Vector3 vertice0(-0.5f, -0.5F, 0);
	Vector3 vertice1(0.5f, 0.5F, 0);
	Vector3 vertice2(0.5f, -0.5F, 0);
	Vector3 vertice3(-0.5f, 0.5F, 0);

	Matrix4x4 mvp = camera->GetProjectionMatrix() * camera->GetViewMatrix() * model;
	//Vector3 tmp = mvp * vertice0;

	Vector4 clipPos0 = mvp * Vector4(vertice0.x, vertice0.y, vertice0.z, 1);
	Vector4 clipPos1 = mvp * Vector4(vertice1.x, vertice1.y, vertice1.z, 1);
	Vector4 clipPos2 = mvp * Vector4(vertice2.x, vertice2.y, vertice2.z, 1);
	Vector4 clipPos3 = mvp * Vector4(vertice3.x, vertice3.y, vertice3.z, 1);

	qDebug() << "clipPos0" << clipPos0;
	qDebug() << "clipPos1" << clipPos1;
	qDebug() << "clipPos2" << clipPos2;
	qDebug() << "clipPos3" << clipPos3;

	Vector3 ndcPos0 = Vector3(clipPos0.x / clipPos0.w, clipPos0.y / clipPos0.w, clipPos0.z / clipPos0.w);
	Vector3 ndcPos1 = Vector3(clipPos1.x / clipPos1.w, clipPos1.y / clipPos1.w, clipPos1.z / clipPos1.w);
	Vector3 ndcPos2 = Vector3(clipPos2.x / clipPos2.w, clipPos2.y / clipPos2.w, clipPos2.z / clipPos2.w);
	Vector3 ndcPos3 = Vector3(clipPos3.x / clipPos3.w, clipPos3.y / clipPos3.w, clipPos3.z / clipPos3.w);

	qDebug() << "ndcPos0" << ndcPos0;
	qDebug() << "ndcPos1" << ndcPos1;
	qDebug() << "ndcPos2" << ndcPos2;
	qDebug() << "ndcPos3" << ndcPos3;

	int x = 0, y = 0, w = 640, h = 360, n = 0.3, f =1000;
	Vector3 screenPos0(w * 0.5f * ndcPos0.x + x + w * 0.5f, h* 0.5f * ndcPos0.y + y + h *0.5f, 0.5f *(f - n) * ndcPos0.z + 0.5f * (f + n));
	Vector3 screenPos1(w * 0.5f * ndcPos1.x + x + w * 0.5f, h* 0.5f * ndcPos1.y + y + h *0.5f, 0.5f *(f - n) * ndcPos1.z + 0.5f * (f + n));
	Vector3 screenPos2(w * 0.5f * ndcPos2.x + x + w * 0.5f, h* 0.5f * ndcPos2.y + y + h *0.5f, 0.5f *(f - n) * ndcPos2.z + 0.5f * (f + n));
	Vector3 screenPos3(w * 0.5f * ndcPos3.x + x + w * 0.5f, h* 0.5f * ndcPos3.y + y + h *0.5f, 0.5f *(f - n) * ndcPos3.z + 0.5f * (f + n));

	qDebug() << "screenPos0" << screenPos0;
	qDebug() << "screenPos1" << screenPos1;
	qDebug() << "screenPos2" << screenPos2;
	qDebug() << "screenPos3" << screenPos3;*/

正交投影

在正交相机中，除了projection矩阵计算和透视相机的计算不一样，其他流程都一样。这里给出正交矩阵的计算代码.

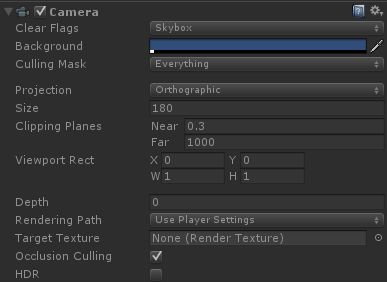
先看Unity，相机参数设置如下

注意一下size指的是

This is half of the vertical size of theviewing volume. Horizontal viewing size varies depending on viewport's aspectratio.

 

正交相机常常用于UI显示。

对于一个640*360的屏幕，size就等于h/2 = 180.

 

这时候得到的透视矩阵是

 

C++代码

Matrix4x4 Transform::OrthoFrustum(float l, float r, float b, float t, float zNear, float zFar)
{
    Matrix4x4 result(0.0f);
    result[0] = 2 / (r - l);
    result[5] = 2 / (t - b);
    result[10] = -2 / (zFar - zNear);
    result[15] = 1;
 
    //result[12] = -(r + l) / (r - l);
    //result[13] = -(t + b) / (t - b);
    result[14] = -(zFar + zNear) / (zFar - zNear);
 
    return result;
}
    Matrix4x4 projection = Transform::OrthoFrustum(0.0f, static_cast(creationFlags.width), 0.0f, static_cast(creationFlags.height), 0.3, 1000);
    qDebug() << "Orthographic ProjectionMatri: " << projection;

 

运行结果

后面计算的流程基本和透视投影的计算一致。

至此，MVP完全搞定！

链接

详解MVP矩阵之齐次坐标和ModelMatrix

详解MVP矩阵之齐次坐标和ViewMatrix

详解MVP矩阵之齐次坐标和ProjectionMatrix