【GNN】NGCF：捕捉协同信号的 GNN

今天学习的是新加坡国立大学和中国科技大学同学合作的论文《Neural Graph Collaborative Filtering》，发表于 2019 年 ACM SIGIR 会议。

Embedding 向量是现代推荐系统的核心，但是目前的方法无法捕捉到 user-item 交互中潜在的协作信号。因此，由此产生的 Embedding 向量可能不足以捕获到协同过滤的内容。

为此，作者提出神经网络协同过滤（Neural Graph Collaborative Filtering，NGCF），旨在将 user-item 的交互信息集成到 Embedding 中，从而在完成二部图的高阶连通性的表达建模。

1.Introduction

一般而言，有两种可学习的协同过滤模型：

1. Embedding：将 user 和 item 转换成向量表示。比如说矩阵分解得到 Embedding，并建模了 user 和 item 之间的交互信息；
2. 交互建模：基于 Embedding 重建历史交互。比如说利用非线性神经网络代替 MF 中的内积或者利用欧几里得作为交互函数；

但这些方法还不足以产生非常好的效果，关键原因在于缺少关键的协作信号（collaborative signal）显示的编码到 Emedding 中，这种信号可以揭示 user（或 item）之间的行为相似性。

虽然这个交互信息很有用，但是想做到这一点绝非易事，特别是在实际应用中，交互规模通常会达到千百万甚至上亿的数据量，从而很难提取所需的协作信号。

本文中，作者通过从 user-item 的交互中探索高阶连接性（high-order connectivity）来解决以上问题。下图阐述了 user-item 的二部图和高阶连接性的概念：

作者设计了一个 Embedding Propagation Layer 通过聚合 user（或 item）的 Embedding 来完善 Embedding 的表达。通过堆叠多个 Embedding Propagation Layer 可以强制 Embedding 捕获到 高阶连通性中的 协同信号。以上图右侧为例，堆叠两层可以捕获 $u_1\leftarrow i_2\leftarrow u_2$ 的行为相似性，堆叠三层可以捕获 $u_1\leftarrow i_2\leftarrow u_2\leftarrow i_4$ 的潜在推荐，同时也可以捕捉到信息的强度（确定 $i_4,i_5$ 的推荐优先级）。

2.NGCF

我们来看下 NGCF 具体内容。

NGCF 总共有三个部分：Embedding Layer、Embedding Propagation Layers 和 Prediction Layer。

2.1 Embedding Layer

Embedding Layer 提供初始化的 user Embedding 和 item Embedding，可以被认为是构建了一个参数矩阵作为 Embedding look-up 表：
$$\mathbf{E}=[\underset{\text{users embedding}}{{\mathbf{e}}_{u_1},\dots ,{\mathbf{e}}_{u_N}},\underset{\text{item embedding}}{{\mathbf{e}}_{i_1},\dots ,{\mathbf{e}}_{i_M}}]$$
该 look-up 表将作为 NGCF 的一部分参与到端到端的优化中，通过多层 Embedding 传播层的优化，可以将协作信号显示注入到 Embedding 中，从而可以产生更加有效的 Embedding 向量。

2.2 Embedding Propagation Layers

接下来我们介绍下消息传递架构，首先考虑单层。

2.2.1 First-order Propagation

交互信息会提供用户偏好的直接证据，类似的，消费了 item 的 user 也可以将该 user 视为该 item 的特征，从而用来衡量两个 item 的协同相似性。在此基础上作者制定了两个操作流程：消息构建（message construction）和消息聚合（message aggregation）。

Message construction

考虑 user-item pair，定义从 i 到 u 的消息传播：
$${\mathbf{m}}_{u\leftarrow i}=f({\mathbf{e}}_i,{\mathbf{e}}_u,p_{ui})$$
其中，$f(\cdot )$ 为消息编码函数，${\mathbf{e}}_i$ ${\mathbf{e}}_u$ 为 Embedding 向量，$p_{ui}$ 用户控制传播的衰减因子。

本文，作者给出 $f(\cdot )$ 为：
$${\mathbf{m}}_{u\leftarrow i}=\frac{1}{\sqrt{\left|{\mathcal{N}}_u\right|\left|{\mathcal{N}}_i\right|}}\left({\mathbf{W}}_1{\mathbf{e}}_i+{\mathbf{W}}_2\left({\mathbf{e}}_i\odot {\mathbf{e}}_u\right)\right)$$
其中，${\mathbf{W}}_1,{\mathbf{W}}_2\in {\mathbb{R}}^{d^{{}^{\prime }}\times d}$ 是可训练的权重矩阵，$d^{{}^{\prime }}$ 为变换大小。

与 GCN 不同的地方在于，这里不仅考虑 ${\mathbf{e}}_i$，同时也会通过 ${\mathbf{e}}_i\odot {\mathbf{e}}_u$ 来编码两者的交互特征，相似的 item 之间会传递更多的信息。这不仅提高了模型的表示能力，还提高了推荐性能。

作者考虑图拉普拉斯范式，令 $p_{ui}=1/\sqrt{|N_u||N_i|}$。从表征角度来说，其反映了历史交互 item 对用户偏好的贡献程度；从消息传递角度来说，可以被认为是一个折扣系数，消息会随着路径的增加而慢慢衰减。

Message aggregation

消息聚合阶段会将用户 u 的邻居传递过来的信息进行聚合并重新表征用户 u，聚合函数为：
$${\mathbf{e}}_u^{(1)}=\text{ LeakyReLU }\left({\mathbf{m}}_{u\leftarrow u}+\sum _{i\in {\mathcal{N}}_u}{\mathbf{m}}_{u\leftarrow i}\right)$$
其中，${\mathbf{e}}_u^{(1)}$ 表示用户 u 通过第一层 Embedding 传播层之后获得的用户表征。${\mathbf{m}}_{u\leftarrow u}={\mathbf{W}}_1{\mathbf{e}}_u$ 会考虑自环，用于保留原始节点的特征信息，并与消息构造共享 ${\mathbf{W}}_1$。

同样的方式，我们也可以得到 ${\mathbf{e}}_i^{(1)}$。

总的来说，Embedding 传播层的优势在于可以显式地利用一阶连通信息来关联 user 和 item 的表征。

2.2.2 High-order Propagation

通过堆叠更多的 Embedding 传播层可以探索高阶连通性，这种高阶连通性对于编码协同信号来估计 user 和 item 之间的相关性非常重要。

堆叠 l 层，我们可以 l-hop 的邻居，如下图所示：

箭头表示信息流，各层的 Embedding 和原始 Embedding 会被拼接得到最终的 Embedding。

user u 的递归公式如下：
$${\mathbf{e}}_u^{(l)}=\text{ LeakyReLU }\left({\mathbf{m}}_{u\leftarrow u}^{(l)}+\sum _{i\in {\mathcal{N}}_u}{\mathbf{m}}_{u\leftarrow i}^{(l)}\right)$$
消息传播定义如下：
$$\{\begin{array}{l}{\mathbf{m}}_{u\leftarrow i}^{(l)}=p_{ui}\left({\mathbf{W}}_1^{(l)}{\mathbf{e}}_i^{(l-1)}+{\mathbf{W}}_2^{(l)}\left({\mathbf{e}}_i^{(l-1)}\odot {\mathbf{e}}_u^{(l-1)}\right)\right)\\ {\mathbf{m}}_{u\leftarrow u}^{(l)}={\mathbf{W}}_1^{(l)}{\mathbf{e}}_u^{(l-1)}\end{array}$$
其中，$\mathbf{W}{1}^{{(l)},\mathbf{W}_{2}}{(l)} \in \mathbb{R}^{d_l \times d{l-1}} $ 为可训练的转移矩阵。

如下图所示，协同信号 $u_1\leftarrow i_2\leftarrow u_2\leftarrow i_4$ 可以通过 Embedding 传播的过程进行捕捉。

规整下之前的公式，我们利用矩阵的形式进行表示：
$${\mathbf{E}}^{(l)}=\mathrm{LeakyReLU}\left((\mathcal{L}+\mathbf{I}){\mathbf{E}}^{(l-1)}{\mathbf{W}}_1^{(l)}+\mathcal{L}{\mathbf{E}}^{(l-1)}\odot {\mathbf{E}}^{(l-1)}{\mathbf{W}}_2^{(l)}\right)$$
其中，$\mathbf{E}^{(l)} \in \mathbb{R}^{(N+M)\times d_l} $ 为 user 和 item 经过 l 步 Embedding 传播后的表征；$\mathbf{I}$ 为单位矩阵；$\mathcal{L}$ 表示二部图的拉普拉斯矩阵：
$$\mathcal{L}={\mathbf{D}}^{-\frac{1}{2}}\mathbf{A}{\mathbf{D}}^{-\frac{1}{2}}\text{ and }\mathbf{A}=\left[\begin{array}{cc}0& \mathbf{R}\\ {\mathbf{R}}^{\top }& 0\end{array}\right]$$
其中，$\mathbf{R}\in R^{N\times M}$ 为 user-item 的交互矩阵；$\mathbf{A}$ 为邻接矩阵；$\mathbf{D}$ 为对角度矩阵；非零对角线 ${\mathcal{L}}_{ui}=1/\sqrt{|N_u||N_i|}$ 与 $q_{ui}$ 相等。

矩阵表示很好解释了 Embedding 的传播过程，也方便我们进行邻居采样。

2.3 Prediction Layer

经过 L 层 Embedding 传播层后，我们会得到 user u 的多层表示，作者将各层表示 concat 到一起：
$${\mathbf{e}}_u^{\ast }={\mathbf{e}}_u^0||\cdot \cdot \cdot ||{\mathbf{e}}_u^L$$
同理 ${\mathbf{e}}_i^{\ast }$。

除了 concat 外，max pooling、LSTM 之类的操作也是支持的。

最终通过向量内积来得到最终的结果：
$${\hat{y}}_{\text{NGCF}}(u,i)={{\mathbf{e}}_u^{\ast }}^T{\mathbf{e}}_i^{\ast }$$

2.4 Optimization

作者采用推荐系统中大量使用的 pairwise BPR loss：
$$Loss=-\sum _{(u,i,j)\in O}\ln \sigma ({\hat{y}}_{ui}-{\hat{y}}_{uj})+\lambda ||\Theta |{|}_2^2$$
其中，$O=\{(u,i,j)|(u,i)\in R^{+},(u,j)\in R^{-}\}$，$R^{+}$ 为观测数据，$R^{-}$ 为未观测数据；$\Theta =\{\mathbf{E},\{{\mathbf{W}}_1^{(l)},{\mathbf{W}}_2^{(l)}{\}}_{l=1}^L\}$ 表示所有可学习的参数；$\lambda$ 控制 L2 正则化的强度从而防止过拟合。

作者采用 mini-batch Adam 进行优化。

此外，作者也会考虑 message dropout 和 node dropout 来增强模型的泛化能力。

3.Experiment

简单看下实验。

所用数据集：

各模型在不同数据集上的表现（NDCG 是搜索排序中的评价指标）：

考虑不同用户稀疏情况下的性能：

不同传播深度的比较：

与不同模型组合后的结果：

不同 message dropout 和 node dropout 参数下的性能结果：

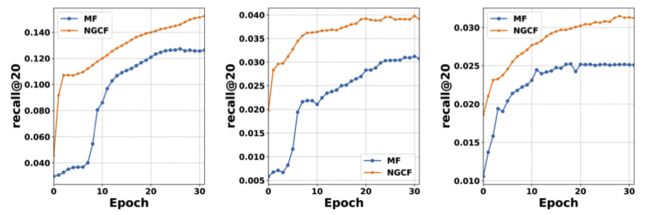
与 MF 进行比较：

可视化结果：

4.Conclusion

总结：作者提出了一个新的框架 NGCF，关键思想在于提出了 Embedding 传播层，并在此基础上充分利用 usr-item 之间的高阶连通性来编码 Embedding 向量。最终，NGCF 在三个真实数据集上取得了不错的成绩。

5.Reference

1. Wang X, He X, Wang M, et al. Neural graph collaborative filtering[C]//Proceedings of the 42nd international ACM SIGIR conference on Research and development in Information Retrieval. 2019: 165-174.

关注公众号跟踪最新内容：阿泽的学习笔记。