Tensorflow2.0 之 SSD 网络结构

引言

SSD 目标检测算法在 2016 年被提出，它的速度要快于 Faster-RCNN，其精度要高于 YOLO（YOLOv3 除外），在本文中，我们主要针对其网络结构进行说明。

网络结构

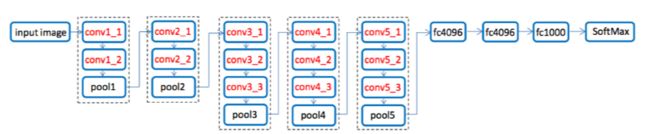
其实 SSD 的网络是基于 VGG 网络来建立的，VGG 网络如下图所示：
SSD 网络将 VGG 中的全连接层去掉后又在后面接了十层卷积层，将 VGG 中的 Conv4_3，新加的 Conv7，Conv8_2，Conv9_2，Conv10_2，Conv11_2 的结果输出，达到多尺度输出（类似于金字塔）的效果，如下图所示：
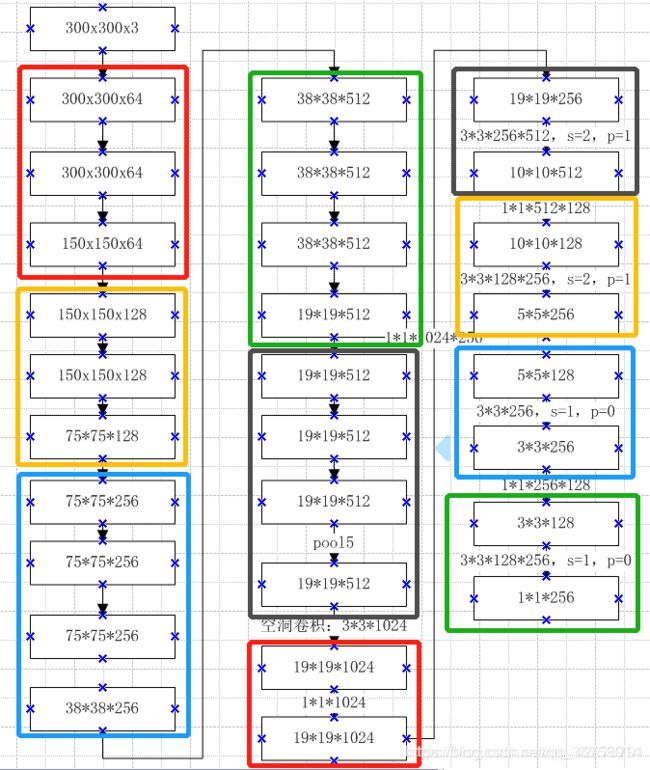
将一张 300x300x3 的图片输入网络，其经历的变换如图所示：
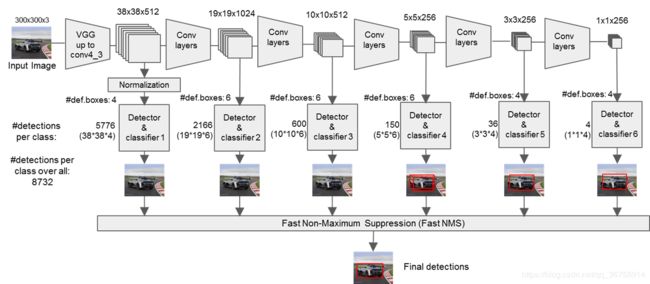我们在不同的特征图上画固定比例的框，大分辨率上的框对检测小目标有帮助，小分辨率上的框对检测大目标有帮助。所以可以得到多个尺度的预测值。

搭建 SSD 网络

import tensorflow as tf
class SSD(tf.keras.Model):
    def __init__(self, num_class=21):
        super(SSD, self).__init__()
        # conv1
        self.conv1_1 = tf.keras.layers.Conv2D(64, 3, activation='relu', padding='same')
        self.conv1_2 = tf.keras.layers.Conv2D(64, 3, activation='relu', padding='same')
        self.pool1   = tf.keras.layers.MaxPooling2D(2, strides=2, padding='same')

        # conv2
        self.conv2_1 = tf.keras.layers.Conv2D(128, 3, activation='relu', padding='same')
        self.conv2_2 = tf.keras.layers.Conv2D(128, 3, activation='relu', padding='same')
        self.pool2   = tf.keras.layers.MaxPooling2D(2, strides=2, padding='same')

        # conv3
        self.conv3_1 = tf.keras.layers.Conv2D(256, 3, activation='relu', padding='same')
        self.conv3_2 = tf.keras.layers.Conv2D(256, 3, activation='relu', padding='same')
        self.conv3_3 = tf.keras.layers.Conv2D(256, 3, activation='relu', padding='same')
        self.pool3   = tf.keras.layers.MaxPooling2D(2, strides=2, padding='same')

        # conv4
        self.conv4_1 = tf.keras.layers.Conv2D(512, 3, activation='relu', padding='same')
        self.conv4_2 = tf.keras.layers.Conv2D(512, 3, activation='relu', padding='same')
        self.conv4_3 = tf.keras.layers.Conv2D(512, 3, activation='relu', padding='same')
        self.pool4   = tf.keras.layers.MaxPooling2D(2, strides=2, padding='same')

        # conv5
        self.conv5_1 = tf.keras.layers.Conv2D(512, 3, activation='relu', padding='same')
        self.conv5_2 = tf.keras.layers.Conv2D(512, 3, activation='relu', padding='same')
        self.conv5_3 = tf.keras.layers.Conv2D(512, 3, activation='relu', padding='same')
        self.pool5   = tf.keras.layers.MaxPooling2D(3, strides=1, padding='same')

        # fc6, => vgg backbone is finished. now they are all SSD blocks
        self.fc6 = tf.keras.layers.Conv2D(1024, 3, dilation_rate=6, activation='relu', padding='same')
        # fc7
        self.fc7 = tf.keras.layers.Conv2D(1024, 1, activation='relu', padding='same')
        # Block 8/9/10/11: 1x1 and 3x3 convolutions strides 2 (except lasts)
        # conv8
        self.conv8_1 = tf.keras.layers.Conv2D(256, 1, activation='relu', padding='same')
        self.conv8_2 = tf.keras.layers.Conv2D(512, 3, strides=2, activation='relu', padding='same')
        # conv9
        self.conv9_1 = tf.keras.layers.Conv2D(128, 1, activation='relu', padding='same')
        self.conv9_2 = tf.keras.layers.Conv2D(256, 3, strides=2, activation='relu', padding='same')
        # conv10
        self.conv10_1 = tf.keras.layers.Conv2D(128, 1, activation='relu', padding='same')
        self.conv10_2 = tf.keras.layers.Conv2D(256, 3, activation='relu', padding='valid')
        # conv11
        self.conv11_1 = tf.keras.layers.Conv2D(128, 1, activation='relu', padding='same')
        self.conv11_2 = tf.keras.layers.Conv2D(256, 3, activation='relu', padding='valid')



    def call(self, x, training=False):
        h = self.conv1_1(x)
        h = self.conv1_2(h)
        h = self.pool1(h)

        h = self.conv2_1(h)
        h = self.conv2_2(h)
        h = self.pool2(h)

        h = self.conv3_1(h)
        h = self.conv3_2(h)
        h = self.conv3_3(h)
        h = self.pool3(h)

        h = self.conv4_1(h)
        h = self.conv4_2(h)
        h = self.conv4_3(h)
        print(h.shape)
        h = self.pool4(h)

        h = self.conv5_1(h)
        h = self.conv5_2(h)
        h = self.conv5_3(h)
        h = self.pool5(h)

        h = self.fc6(h)     # [1,19,19,1024]
        h = self.fc7(h)     # [1,19,19,1024]
        print(h.shape)

        h = self.conv8_1(h)
        h = self.conv8_2(h) # [1,10,10, 512]
        print(h.shape)

        h = self.conv9_1(h)
        h = self.conv9_2(h) # [1, 5, 5, 256]
        print(h.shape)

        h = self.conv10_1(h)
        h = self.conv10_2(h) # [1, 3, 3, 256]
        print(h.shape)

        h = self.conv11_1(h)
        h = self.conv11_2(h) # [1, 1, 1, 256]
        print(h.shape)
        return h

当我们将一张 300x300x3 的图片输入，得到的结果为：

model = SSD(21)
x = model(tf.ones(shape=[1,300,300,3]))

(1, 38, 38, 512)
(1, 19, 19, 1024)
(1, 10, 10, 512)
(1, 5, 5, 256)
(1, 3, 3, 256)
(1, 1, 1, 256)

空洞卷积

在以上代码中构建 self.fc6 这层卷积层时，我们使用了空洞卷积（dilated convolution），这引入了一个新的参数，即扩张率（dilation rate），其原理如图所示：
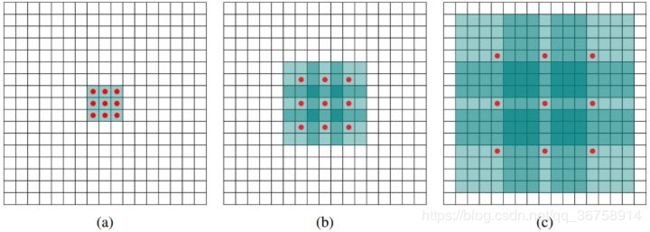a 图对应扩张率为 1 时的 3x3 卷积核，其实就和普通的卷积操作一样，b 图对应扩张率为 2 时的 3x3 卷积核，也就是对于图像中一个 7x7 的区域，只有 9 个红色的点和 3x3 的卷积核发生卷积操作，其余的点略过。也可以理解为卷积核大小为 7x7，但是只有图中的 9 个点的权重不为 0，其余都为 0。 可以看到虽然卷积核大小只有 3x3，但是这个卷积的感受野已经增大到了 7x7，c 图对应扩张率为 4 时的 3x3 卷积核，能达到15x15的感受野。对比传统的conv操作，3层3x3的卷积加起来，stride为1的话，只能达到 (kernel-1)xlayer+1=7 的感受野，也就是和层数成线性关系，而空洞卷积的感受野是指数级的增长。

参考资料

目标检测之经典网络SSD解读
彻底搞懂SSD网络结构