Apriori算法整理

实践课题报告： Apriori算法

学 校：xxx大学

学 院：大数据与智能工程学院

专 业：信息工程（数据科学与大数据技术）

年 级：2017级

姓 名：xxx

指导老师：xxx

日 期：2019 年 6 月 24 日

一、简介

关联规则学习（Association rule learning）是一种在大型数据库中发现变量之间的有趣性关系的方法。它的目的是利用一些有趣性的量度来识别数据库中发现的强规则。
关联分析是一种在大规模数据集中寻找有趣关系的任务。这些关系可以有两种形式:频繁项 集或者关联规则。频繁项集(frequent item sets)是经常出现在一块的物品的集合,关联规则(association rules)暗示两种物品之间可能存在很强的关系。
这些关系可以有两种形式：频繁项集、关联规则。

频繁项集：经常出现在一块的物品的集合

关联规则：暗示两种物品之间可能存在很强的关系

二、挖掘步骤：

1.依据支持度找出所有频繁项集（频度）

2.依据置信度产生关联规则（强度）

三、基本概念

对于A->B

①支持度（support）：P(A ∩ B)，既有A又有B的概率： 

support({A,B}) = num(A∪B) / W = P(A∩B)
num(A∪B)表示含有物品集{A,B}的事务集的个数，不是数学中的并集。


②置信度（Confidence）：

P(B|A)，在A发生的事件中同时发生B的概率 p(AB)/P(A)：

Confidence(A->B) = support({A,B}) / support({A}) = P(B|A)     

例如购物车分析：牛奶 ⇒ 面包

例子：[支持度：3%，置信度：40%]

支持度3%：意味着3%顾客同时购买牛奶和面包

置信度40%：意味着购买牛奶的顾客40%也购买面包


③如果事件A中包含k个元素，那么称这个事件A为k项集事件A满足
最小支持度阈值的事件称为频繁k项集


④同时满足最小支持度阈值和最小置信度阈值的规则称为强规则

四、基本原理

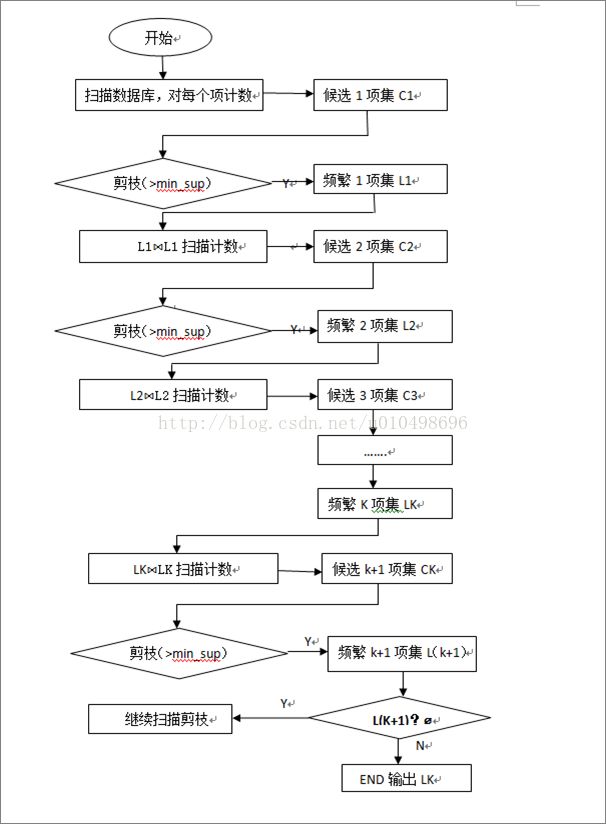
apriori算法使用一种成为逐层搜索的迭代算法，其中k项集用于探索（k+1）项集。首先，通过扫描数据库，累计每个项的计数，并搜集满足最小支持度的项，找出频繁1项集的集合。该集合记为L1。然后，使用L1找出频繁2项集的集合L2，使用L2找出L3，如此下去，直到不能再找到频繁k项集。

该算法基本思路计算复杂度是非常大的。为了提高频繁项集的产生效率，使用先验性质（频繁项集的所有非空子集也一定是频繁的；换句话说，若某个集合存在一个非空子集不是频繁项集，则该集合不是频繁项集）来压缩搜索空间。

如何在算法中使用先验性质？为了理解这一点，我们考察如何使用Lk-1找出Lk，其中k>=2。主要由两步构成：连接步和剪枝步。

连接步：为找出Lk，通过将Lk-1与自身相连接产生候选集k项集的集合。该候选集的集合记为Ck。设l1和l2是Lk-1中的项集。记号li[j]表示li的第j项（例如，l1[k-2]表示l1的倒数第2项）。为了有效实现，apriori算法假定事务或项集中的项按字典序排列。对于（k-1）项集li，这意味着把项排序，使得li[1]（l1[2]=l2[2]）…^{（l1[k-2]=l2[k-2]）}（l1[k-1]

剪枝步： CK是LK的超集，也就是说，CK的成员可能是也可能不是频繁的。通过扫描所有的事务（交易），确定CK中每个候选的计数，判断是否小于最小支持度计数，如果不是，则认为该候选是频繁的。为了压缩Ck,可以利用Apriori性质：任一频繁项集的所有非空子集也必须是频繁的，反之，如果某个候选的非空子集不是频繁的，那么该候选肯定不是频繁的，从而可以将其从CK中删除。（该步利用了标红的先验性质）。

五、Java实现

运行环境：

1.eclipse开发工具
2.MySQL数据库

1、 伪代码

算法：Apriori
	输入：D - 事务数据库；min_sup - 最小支持度计数阈值
	输出：L - D中的频繁项集
	方法：
		 L1=find_frequent_1-itemsets(D); // 找出所有频繁1项集
		 For(k=2;Lk-1!=null;k++){
			Ck=apriori_gen(Lk-1); // 产生候选，并剪枝
			For each 事务t in D{ // 扫描D进行候选计数
				Ct =subset(Ck,t); // 得到t的子集
				For each 候选c 属于 Ct
							 c.count++;
			}
			Lk={c属于Ck | c.count>=min_sup}
	}
	Return L=所有的频繁集；

	Procedure apriori_gen(Lk-1:frequent(k-1)-itemsets)
		  For each项集l1属于Lk-1
				  For each项集 l2属于Lk-1
						   If((l1[1]=l2[1])&&( l1[2]=l2[2])&&…….
	&& (l1[k-2]=l2[k-2])&&(l1[k-1]

2、Apriori算法Java代码

        package com.yumo.machine.learning.algorithms;
        import java.util.ArrayList;
        import java.util.HashMap;
        import java.util.List;
        import java.util.Map;
        import java.util.Set;

        public class Apriori{
            // 支持度阈值
            private final static int SUPPORT = 2;
            // 置信度阈值
            private final static double CONFIDENCE = 0.7;
            // 项之间的分隔符
            private final static String GAP = ";";
             // 项之间的分隔符
            private final static String CON = "-->";

            /**
             * 这个是用来找出1-频繁项集的方法，因为1-频繁项集的特殊性，
             * 所以需要特别的方法来返回1-频繁项集
             * @param dataList
             * @return
             */

            private Map find1_FrequentSet(ArrayList dataList){
                Map resultSetMap = new HashMap<>();
                for (String data:dataList) {
                    String [] strings = data.split(GAP);
                    //这是把所有的购买记录一条条的筛选出来
                    for (String string : strings) {
                        string += GAP;
                        if (resultSetMap.get(string)==null) {
                            resultSetMap.put(string,1);
                        }
                        else {
                            resultSetMap.put(string, resultSetMap.get(string)+1);
                        }
                    }
                }
                //返回的是一个各种商品对应出现频次的Map（或可称之为频繁项集）。键为商品序号，值为出现次数。
                return resultSetMap;    
            }

            /**
             * 使用先验知识，判断候选集是否是频繁项集
             * @param candidate
             * @param setMap
             * @return
             */

            private boolean hasInfrequentSubset(String candidateString, Map setMap){
                String[] strings = candidateString.split(GAP);
                //找出候选集所有的子集，并判断每个子集是否属于频繁子集
                for (int i=0; i aprioriGen(Map setMap){
                //此处传入的参数就是上面返回的频繁项集。
                Map candidateSetMap = new HashMap<>();
                // 对每个商品取集合
                Set candidateSet = setMap.keySet();
                //单独考虑每个商品的支持度，如果合格，就可以进行拼接。否则丢掉。
                for (String s1 : candidateSet) {
                    String[] strings1 = s1.split(GAP);
                    String s1string = "";
                    for (String temp : strings1) {
                        s1string += temp+GAP;
                    }
                    for (String s2 :  candidateSet) {
                        //此处也是默认商品序号是有序的。这样先判定前len-1项是否相等。
                        //如果前面相等，第len项不相等，那么就可以拼接成len+1长度的候选集了。
                        String[] strings2 = s2.split(GAP);
                        boolean flag = true;
                        for (int i=0; i< strings1.length-1;++i) {
                            if (strings1[i].compareTo(strings2[i]) != 0) {
                                flag = false;
                                break;
                            }
                        }
                        if (flag && strings1[strings1.length-1].compareTo(strings2[strings2.length-1])<0) {
                           //连接步：产生候选
                           String c=s1string+strings2[strings2.length-1]+GAP;
                           if (hasInfrequentSubset(c,setMap)) {
                                //剪枝步：删除非频繁的候选
                            } 
                            else {
                                candidateSetMap.put(c,0);
                            }
                        }
                    }
                }
                return candidateSetMap;
            }

            /**
             * 算法主程序
             * @param dataList
             * @return
             */

            public Map apriori(ArrayList dataList){
                Map setpFrequentSetMap = new HashMap<>();
                setpFrequentSetMap.putAll(find1_FrequentSet(dataList));

                Map frequentSetMap = new HashMap();
                frequentSetMap.putAll(setpFrequentSetMap);
                // Into the loop choose
                while(setpFrequentSetMap!=null && setpFrequentSetMap.size() > 0){
                    Map candidateSetMap = aprioriGen(setpFrequentSetMap);
                    //得到的就是候选集 candidateSetMap ，当然我们只要key部分即可啦！
                    Set candidateKeySet = candidateSetMap.keySet();

                    //扫描D，进行计数
                    for (String data : dataList) {
                        for (String candidate :  candidateKeySet) {
                            boolean flag = true;
                            String[] strings = candidate.split(GAP);
                            for (String string : strings) {
                                //意味着在Data，也就是在初始的购物记录中查找当前的频繁项集中的某一条。寻找string如果不成功，则返回-1；
                                // indexOf(Object o)方法 
                                // 功能：查找某个元素在ArrayList中第一次出现的位置。
                                if (data.indexOf(string+GAP)==-1) {
                                    flag = false;
                                    break;
                                }
                            }
                            //如果查找成功，那么就可以丢到正式的候选集中了。
                            if (flag) {
                                candidateSetMap.put(candidate,candidateSetMap.get(candidate)+1);
                            }
                        }
                    }
                    //从候选集中找到符合支持度的频繁项集，stepFrequentSetMap顾名思义就是每一次找到的新的频繁集。
                    //所以在置入新的频繁集之前，都要先把上次的清空掉。
                    setpFrequentSetMap.clear();
                    for (String candidate : candidateKeySet) {
                        Integer count = candidateSetMap.get(candidate);
                        if (count>=SUPPORT) {
                            setpFrequentSetMap.put(candidate,count);
                        }
                    }
                    // puaAll的作用是把一个Map的所有元素置入并且去重。
                    // 合并所有频繁集
                    frequentSetMap.putAll(setpFrequentSetMap);
                }
                //While循环结束的条件是新的频繁项集的大小为0.也就是必须要完全空了才出来。
                //这时候已经确保了frequentSetMap包含有所有的频繁项集了。
                return frequentSetMap;
            }
            /**
             * 求一个集合所有的非空真子集
             * 
             * @param sourceSet
             * @return
             * 为了以后可以用在其他地方，这里我们不是用递归的方法
             * 
             *
             * 思路：假设集合S（A,B,C,D），其大小为4，拥有2的4次方个子集，即0-15，二进制表示为0000，0001，...，1111。
             * 对应的子集为空集，{D}，...，{A,B,C,D}。
             */

            private List subset(String sourceSet){
                //“按位对应法”,从1-2^strings.length-1位，可以用二进制来表示是否取到该值。
                /*
                如集合A={a,b,c},对于任意一个元素，在每个子集中，要么存在，要么不存在。 映射为子集：
                (a,b,c)
                (1,1,1)->(a,b,c)
                (1,1,0)->(a,b)
                (1,0,1)->(a,c)
                (1,0,0)->(a)
                (0,1,1)->(b,c)
                (0,1,0)->(b)
                (0,0,1)->(c)
                (0,0,0)->@(@表示空集)
                */
                List result = new ArrayList<>();
                String[] strings = sourceSet.split(GAP);
                for (int i = 1; i<(Math.pow(2,strings.length)) - 1; ++i ) {
                    String item = "";
                    int ii = i;
                    int[] flag = new int[strings.length]; 
                    int count = 0;
                    while(ii>=0 && count getRelationRules(Map frequentSetMap){
                Map relationMap = new HashMap<>();
                Set KeySet = frequentSetMap.keySet();
                for (String key : KeySet) {
                    List keySubset = subset(key);
                    for (String keySubSetItem : keySubset) {
                        //子集keySubsetItem也是频繁项
                        Integer count = frequentSetMap.get(keySubSetItem);
                        if (count!=null) {
                             /*
                             置信度：
                             置信度(confidence)揭示了A出现时B是否一定出现，如果出现，则出现的概率是多大。如果A->B的置信度是100%，则说明A出现时B一定会出现（返回来不一定）。
                                上图中底板共出现5次，其中4次同时购买了胶皮，底板->胶皮的置信度是80%。
                             用公式表示是，物品A->B的置信度=物品{A,B}的支持度 / 物品{A}的支持度：
                             Confidence(A->B) = support({A,B}) / support({A}) = P(B|A)
                            */ 
                            Double confidence = (1.0*frequentSetMap.get(key))/(1.0*frequentSetMap.get(keySubSetItem));
                            if (confidence > CONFIDENCE) {
                                relationMap.put(keySubSetItem+CON+expect(key,keySubSetItem),confidence);
                            }
                        }
                    }
                }   
                return relationMap;
            }

        }


#### 3、测试

#####  数据库连接类

    package com.crop.jdbc;

    import java.sql.DriverManager;
    import java.sql.ResultSet;
    import java.sql.SQLException;

    import java.sql.Connection;
    import java.sql.Statement;

    /** 
     * ClassName: DBUtil
     * @Description: TODO 连接数据库
     * @author zhangkaifu
     */
    public class DBUtil {

        // 数据库连接对象
        private static Connection conn=null; 

        // 数据库连接地址
        private static String URL = "jdbc:mysql://localhost:3306/data?characterEncoding=utf8&useSSL=true";

        // 数据库的用户名
        private static String UserName = "root";
        // 数据库的密码
        private static String Password = "mysqldata";

        /**
         * * @Description: TODO 获取访问数据库的Connection对象
         * @param @return
         * @return Connection 连接数据的对象
         * @author zhangkaifu
         */
        public static Connection getConnection() {

            try {

                Class.forName("com.mysql.jdbc.Driver"); // 加载驱动

                System.out.println("加载驱动成功!!!");
            } catch (ClassNotFoundException e) {
                // TODO: handle exception
                e.printStackTrace();
            }

            try {

                //通过DriverManager类的getConenction方法指定三个参数,连接数据库
                conn = (Connection)DriverManager.getConnection(URL, UserName, Password);
                System.out.println("连接数据库成功!!!");

                //返回连接对象
                return conn;

            } catch (SQLException e) {
                // TODO: handle exception
                e.printStackTrace();
                return null;
            }
        }

    }

数据库辅助类

    package com.yumo.machine.learning.algorithms.data;

    import java.sql.Connection;
    import java.sql.PreparedStatement;
    import java.sql.ResultSet;
    import java.sql.SQLException;
    import java.sql.Statement;
    import java.util.ArrayList;

    /** 
     * ClassName:  DBhelper
     * @Description: TODO 数据库辅助类
     * @author zhangkaifu
     */
    public class DBhelper {
        // 获取类中可以共用的对象
            private static Connection conn = null;
            private static PreparedStatement ps = null;
            private static ResultSet rs = null;
            // 代码运行时即开始连接数据库
            static {
                conn = DBUtil.getConnection();
            }
        /**
         * Description:放全部资源
         * @param conn
         * @param ps
         * @param rs
         * @throws SQLException
         */
            public static void closeAll(Connection conn, Statement ps, ResultSet rs)
                    throws SQLException {
                if (conn != null) {
                    conn.close();
                }
                if (ps != null) {
                    ps.close();
                }
                if (rs != null) {
                    rs.close();
                }
            }

            // 释放所用资源
            public static void closePart(Connection conn, Statement stt)
                    throws SQLException {
                if (conn != null) {
                    conn.close();
                }
                if (stt != null) {
                    stt.close();
                }
            }
            // 查询元素
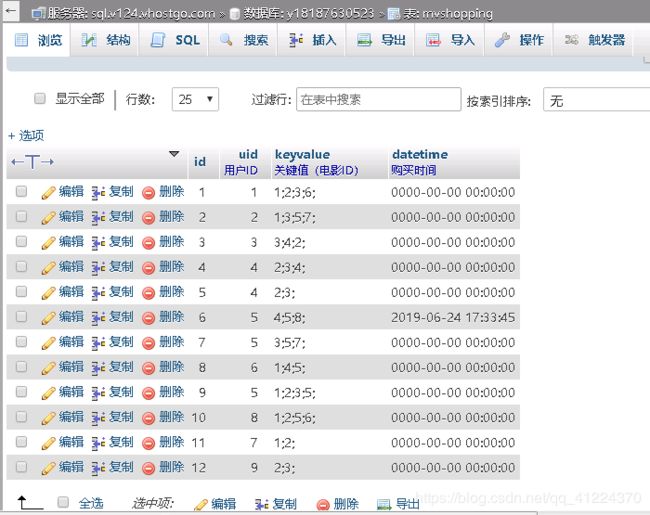
            public static ArrayList selectAll() {
                ArrayList data = new ArrayList<>();
                String sql = "select keyvalue from mvshopping";
                try {
                    ps = conn.prepareStatement(sql);
                    rs = ps.executeQuery();// 执行sql
                    // 遍厉打印元素
                    while (rs.next()) {
                        data.add(rs.getString("keyvalue"));// 将对象添加到集合中
                    }
                } catch (SQLException e) {
                    System.out.println("数据获取失败！！！！");;
                } finally {
                    try {
                        DBhelper.closeAll(conn, ps, rs);
                    } catch (SQLException e) {
                        e.printStackTrace();
                    }
                }
                return data;
            }
    }

数据集

数据集保存在数据库中，内容如下。

测试主函数

    package com.yumo.machine.learning.algorithms.test;

    import java.util.ArrayList;
    import java.util.Map;
    import java.util.Set;

    import com.yumo.machine.learning.algorithms.Apriori;
    import com.yumo.machine.learning.algorithms.data.DBhelper;

    public class test {
        public static void main(String[] args)
        {
            ArrayList dataList = new ArrayList<>();
            //从数据库获取数据
            dataList = DBhelper.selectAll();
            System.out.println("***数据集合**********");
            for(String string:dataList)
            {
                System.out.println(string);
            }

            Apriori apriori = new Apriori();

            System.out.println("***频繁项集**********");

            Map frequentSetMap = apriori.apriori(dataList);
            Set keySet = frequentSetMap.keySet();
            for(String key:keySet)
            {
                System.out.println(key+" : "+frequentSetMap.get(key));
            }

            System.out.println("***关联规则**********");
            Map relationRulesMap = apriori.getRelationRules(frequentSetMap);
            Set rrKeySet = relationRulesMap.keySet();
            for (String rrKey : rrKeySet)
            {
                System.out.println(rrKey + "  :  " + relationRulesMap.get(rrKey));
            }

        }

    }

运行结果

六、算法分析

1、时间复杂度

在进行算法分析时，语句总的执行次数T(n)是关于问题规模n的函数，进而分析T(n)随n的变化情况并确定T(n)的数量级。算法的时间复杂度，也就是算法的时间量度，记作：T(n)= O(f(n))。它表示随问题规模n的增大，算法执行时间的增长率和f(n)的增长率相同，称作算法的渐近时间复杂度，简称为时间复杂度，是一种“渐进表示法”。其中f(n)是问题规模n的某个函数。

用大写O()来体现算法时间复杂度的记法，我们称之为大O记法。

一般情况下，随着输入规模n的增大，T(n)增长最慢的算法为最优算法。
显然，由此算法时间复杂度的定义可知，我们的三个求和算法的时间复杂度分别为O(1)，O(n)，O(n^2) 。。。。。

分析如下

方法（函数）find1_FrequentSet的时间复杂度为：

T（n) = O(n^2)

代码如下：|

    private Map find1_FrequentSet(ArrayList dataList){
            Map resultSetMap = new HashMap<>();
            for (String data:dataList) {
                String [] strings = data.split(GAP);
                //这是把所有的购买记录一条条的筛选出来
                for (String string : strings) {
                    string += GAP;
                    if (resultSetMap.get(string)==null) {
                        resultSetMap.put(string,1);
                    }
                    else {
                        resultSetMap.put(string, resultSetMap.get(string)+1);
                    }
                }
            }
            //返回的是一个各种商品对应出现频次的Map（或可称之为频繁项集）。键为商品序号，值为出现次数。
            return resultSetMap;    
        }

方法（函数） hasInfrequentSubset的时间复杂度为：

T（n) = O(n^2)

代码如下：|

     /**
         * 使用先验知识，判断候选集是否是频繁项集
         * @param candidate
         * @param setMap
         * @return
         */

        private boolean hasInfrequentSubset(String candidateString, Map setMap){
            String[] strings = candidateString.split(GAP);
            //找出候选集所有的子集，并判断每个子集是否属于频繁子集
            for (int i=0; i

方法（函数） sourceSet的时间复杂度为：

T（n) = O(n^2)

代码如下：|

    /**
         * 求一个集合所有的非空真子集
         * 
         * @param sourceSet
         * @return
         * 为了以后可以用在其他地方，这里我们不是用递归的方法
         * 
         * 
         * 思路：假设集合S（A,B,C,D），其大小为4，拥有2的4次方个子集，即0-15，二进制表示为0000，0001，...，1111。
         * 对应的子集为空集，{D}，...，{A,B,C,D}。
         */

        private List subset(String sourceSet){
            //“按位对应法”,从1-2^strings.length-1位，可以用二进制来表示是否取到该值。
            /*
            如集合A={a,b,c},对于任意一个元素，在每个子集中，要么存在，要么不存在。 映射为子集：
            (a,b,c)
            (1,1,1)->(a,b,c)
            (1,1,0)->(a,b)
            (1,0,1)->(a,c)
            (1,0,0)->(a)
            (0,1,1)->(b,c)
            (0,1,0)->(b)
            (0,0,1)->(c)
            (0,0,0)->@(@表示空集)
            */
            List result = new ArrayList<>();
            String[] strings = sourceSet.split(GAP);
            for (int i = 1; i<(Math.pow(2,strings.length)) - 1; ++i ) {
                String item = "";
                int ii = i;
                int[] flag = new int[strings.length]; 
                int count = 0;
                while(ii>=0 && count

方法（函数） expect的时间复杂度为：

T（n) = O(n^2)

代码如下：|

    /**
         * 集合运算，A/B
         * @param A
         * @param B
         * @return
         */
        private String expect(String stringA, String stringB){
            String result = "";
            String[] stringAs = stringA.split(GAP);
            String[] stringBs = stringB.split(GAP);

            for(int i=0; i

方法（函数） frequentSetMap 中嵌套调用了expect和subset方法，综合分析其时间复杂度为：

T（n) = O(n^4)

代码如下：|

    /**
         * 由频繁项集产生关联规则
         * @param frequentSetMap
         * @return
         */
        public Map getRelationRules(Map frequentSetMap){
            Map relationMap = new HashMap<>();
            Set KeySet = frequentSetMap.keySet();
            for (String key : KeySet) {
                List keySubset = subset(key);
                for (String keySubSetItem : keySubset) {
                    //子集keySubsetItem也是频繁项
                    Integer count = frequentSetMap.get(keySubSetItem);
                    if (count!=null) {
                         /*
                         置信度：
                         置信度(confidence)揭示了A出现时B是否一定出现，如果出现，则出现的概率是多大。如果A->B的置信度是100%，则说明A出现时B一定会出现（返回来不一定）。
                            上图中底板共出现5次，其中4次同时购买了胶皮，底板->胶皮的置信度是80%。
                         用公式表示是，物品A->B的置信度=物品{A,B}的支持度 / 物品{A}的支持度：
                         Confidence(A->B) = support({A,B}) / support({A}) = P(B|A)
                        */ 
                        Double confidence = (1.0*frequentSetMap.get(key))/(1.0*frequentSetMap.get(keySubSetItem));
                        if (confidence > CONFIDENCE) {
                            relationMap.put(keySubSetItem+CON+expect(key,keySubSetItem),confidence);
                        }
                    }
                }
            }   
            return relationMap;
        }

   方法（函数） aprioriGen的时间复杂度为：
   
   ### T（n)  = O(n^3)
   
   代码如下：|

     /**
         * 根据上面的频繁项集的集合选出候选集
         * @param setMap
         * @return
         */
        private Map aprioriGen(Map setMap){
            //此处传入的参数就是上面返回的频繁项集。
            Map candidateSetMap = new HashMap<>();
            // 对每个商品取集合
            Set candidateSet = setMap.keySet();
            //单独考虑每个商品的支持度，如果合格，就可以进行拼接。否则丢掉。
            for (String s1 : candidateSet) {
                String[] strings1 = s1.split(GAP);
                String s1string = "";
                for (String temp : strings1) {
                    s1string += temp+GAP;
                }
                for (String s2 :  candidateSet) {
                    //此处也是默认商品序号是有序的。这样先判定前len-1项是否相等。
                    //如果前面相等，第len项不相等，那么就可以拼接成len+1长度的候选集了。
                    String[] strings2 = s2.split(GAP);
                    boolean flag = true;
                    for (int i=0; i< strings1.length-1;++i) {
                        if (strings1[i].compareTo(strings2[i]) != 0) {
                            flag = false;
                            break;
                        }
                    }
                    if (flag && strings1[strings1.length-1].compareTo(strings2[strings2.length-1])<0) {
                       //连接步：产生候选
                       String c=s1string+strings2[strings2.length-1]+GAP;
                       if (hasInfrequentSubset(c,setMap)) {
                            //剪枝步：删除非频繁的候选
                        } 
                        else {
                            candidateSetMap.put(c,0);
                        }
                    }
                }
            }
            return candidateSetMap;
        }

方法（函数） apriori 中还嵌套调用了 aprioriGen方法，综合分析故其时间复杂度为：

T（n) = O(n^4)

代码如下：|

/**
     * 算法主程序
     * @param dataList
     * @return
     */

    public Map apriori(ArrayList dataList){
        Map setpFrequentSetMap = new HashMap<>();
        setpFrequentSetMap.putAll(find1_FrequentSet(dataList));

        Map frequentSetMap = new HashMap();
        frequentSetMap.putAll(setpFrequentSetMap);
        // Into the loop choose
        while(setpFrequentSetMap!=null && setpFrequentSetMap.size() > 0){
            Map candidateSetMap = aprioriGen(setpFrequentSetMap);
            //得到的就是候选集 candidateSetMap ，当然我们只要key部分即可啦！
            Set candidateKeySet = candidateSetMap.keySet();

            //扫描D，进行计数
            for (String data : dataList) {
                for (String candidate :  candidateKeySet) {
                    boolean flag = true;
                    String[] strings = candidate.split(GAP);
                    for (String string : strings) {
                        //意味着在Data，也就是在初始的购物记录中查找当前的频繁项集中的某一条。寻找string如果不成功，则返回-1；
                        // indexOf(Object o)方法 
                        // 功能：查找某个元素在ArrayList中第一次出现的位置。
                        if (data.indexOf(string+GAP)==-1) {
                            flag = false;
                            break;
                        }
                    }
                    //如果查找成功，那么就可以丢到正式的候选集中了。
                    if (flag) {
                        candidateSetMap.put(candidate,candidateSetMap.get(candidate)+1);
                    }
                }
            }
            //从候选集中找到符合支持度的频繁项集，stepFrequentSetMap顾名思义就是每一次找到的新的频繁集。
            //所以在置入新的频繁集之前，都要先把上次的清空掉。
            setpFrequentSetMap.clear();
            for (String candidate : candidateKeySet) {
                Integer count = candidateSetMap.get(candidate);
                if (count>=SUPPORT) {
                    setpFrequentSetMap.put(candidate,count);
                }
            }
            // puaAll的作用是把一个Map的所有元素置入并且去重。
            // 合并所有频繁集
            frequentSetMap.putAll(setpFrequentSetMap);
        }
        //While循环结束的条件是新的频繁项集的大小为0.也就是必须要完全空了才出来。
        //这时候已经确保了frequentSetMap包含有所有的频繁项集了。
        return frequentSetMap;
    }

综合上述分析，Apriori算法的时间复杂度为: T(n) = O(n^4)

2、空间复杂度

算法的空间复杂度通过计算算法所需的存储空间实现，算法的空间复杂度的计算公式记作：S(n)=O(f(n))，其中，n为问题的规模，f(n)为语句关于n所占存储空间的函数，也是一种“渐进表示法”，这些所需要的内存空间通常分为“固定空间内存”（包括基本程序代码、常数、变量等）和“变动空间内存”（随程序运行时而改变大小的使用空间）

通常，我们都是用“时间复杂度”来指运行时间的需求，是用“空间复杂度”指空间需求。

计算方法
忽略常数，用O(1)表示
递归算法的空间复杂度=递归深度N*每次递归所要的辅助空间
对于单线程来说，递归有运行时堆栈，求的是递归最深的那一次压栈所耗费的空间的个数，因为递归最深的那一次所耗费的空间足以容纳它所有递归过程。

从测试函数来分析空间复杂度

    public static void main(String[] args)
        {
            ArrayList dataList = new ArrayList<>();
            //从数据库获取数据
            dataList = DBhelper.selectAll();
            System.out.println("***数据集合**********");
            for(String string:dataList)
            {
                System.out.println(string);
            }

            Apriori apriori = new Apriori();

            System.out.println("***频繁项集**********");

            Map frequentSetMap = apriori.apriori(dataList);
            Set keySet = frequentSetMap.keySet();
            for(String key:keySet)
            {
                System.out.println(key+" : "+frequentSetMap.get(key));
            }

            System.out.println("***关联规则**********");
            Map relationRulesMap = apriori.getRelationRules(frequentSetMap);
            Set rrKeySet = relationRulesMap.keySet();
            for (String rrKey : rrKeySet)
            {
                System.out.println(rrKey + "  :  " + relationRulesMap.get(rrKey));
            }

        }

从以上代码来看， 主要的存储空间是 对dataList，frequentSetMap，keySet，relationRulesMap，rrKeySet的数据的存储，

综合考虑分析，算法的空间复杂度级别为：

S(n) = 5*n *O(n)

七、应用场景

经典的关联规则数据挖掘算法Apriori 算法广泛应用于各种领域，通过对数据的关联性进行了分析和挖掘，挖掘出的这些信息在决策制定过程中具有重要的参考价值。
Apriori算法广泛应用于商业中，应用于消费市场价格分析中，它能够很快的求出各种产品之间的价格关系和它们之间的影响。通过数据挖掘，市场商人可以瞄准目标客户，采用个人股票行市、最新信息、特殊的市场推广活动或其他一些特殊的信息手段，从而极大地减少广告预算和增加收入。百货商场、超市和一些老字型大小的零售店也在进行数据挖掘，以便猜测这些年来顾客的消费习惯。
Apriori算法应用于网络安全领域，比如网络入侵检测技术中。早期中大型的电脑系统中都收集审计信息来建立跟踪档，这些审计跟踪的目的多是为了性能测试或计费，因此对攻击检测提供的有用信息比较少。它通过模式的学习和训练可以发现网络用户的异常行为模式。采用作用度的Apriori算法削弱了Apriori算法的挖掘结果规则，是网络入侵检测系统可以快速的发现用户的行为模式，能够快速的锁定攻击者，提高了基于关联规则的入侵检测系统的检测性。
Apriori算法应用于高校管理中。随着高校贫困生人数的不断增加，学校管理部门资助工作难度也越加增大。针对这一现象，提出一种基于数据挖掘算法的解决方法。将关联规则的Apriori算法应用到贫困助学体系中，并且针对经典Apriori挖掘算法存在的不足进行改进，先将事务数据库映射为一个布尔矩阵，用一种逐层递增的思想来动态的分配内存进行存储，再利用向量求"与"运算，寻找频繁项集。实验结果表明，改进后的Apriori算法在运行效率上有了很大的提升，挖掘出的规则也可以有效地辅助学校管理部门有针对性的开展贫困助学工作。
Apriori算法被广泛应用于移动通信领域。移动增值业务逐渐成为移动通信市场上最有活力、最具潜力、最受瞩目的业务。随着产业的复苏，越来越多的增值业务表现出强劲的发展势头，呈现出应用多元化、营销品牌化、管理集中化、合作纵深化的特点。针对这种趋势，在关联规则数据挖掘中广泛应用的Apriori算法被很多公司应用。依托某电信运营商正在建设的增值业务Web数据仓库平台，对来自移动增值业务方面的调查数据进行了相关的挖掘处理，从而获得了关于用户行为特征和需求的间接反映市场动态的有用信息，这些信息在指导运营商的业务运营和辅助业务提供商的决策制定等方面具有十分重要的参考价值。

应用实列

穿衣搭配是服饰鞋包导购中非常重要的课题，基于搭配专家和达人生成的搭配组合数据，百万级别的商品的文本和图像数据，以及用户的行为数据。期待能从以上行为、文本和图像数据中挖掘穿衣搭配模型，为用户提供个性化、优质的、专业的穿衣搭配方案，预测给定商品的搭配商品集合。

八、结语

Apriori算法是一种挖掘关联规则的频繁项集算法，其核心思想是通过候选集生成和情节的向下封闭检测两个阶段来挖掘频繁项集。主要用于做快速的关联规则分析。Apriori算法在世界上广为流传，得到极大的关注。Apriori算法已经被广泛的应用到商业、网络安全、高校管理和移动通信等领域。