通俗全面理解图卷积与GCN网络(二):从图卷积到GCN
上一篇:通俗全面理解图卷积与GCN网络(一):图与图卷积
目录
- 前言
- 卷积
- 傅里叶变换
- 信号的傅里叶变换
- 图的傅里叶变换
- 图卷积
- GCN(图卷积神经网络)
- 第一代GCN
- 第二代GCN
- 总结
前言
在上一篇文章中我们介绍了图的部分概念以及最简单的图卷积方式,但这里的图卷积在实现起来还存在着一些问题,在这一篇文章中我们从卷积的定义角度导出图上的卷积,再将它用到GCN里。
卷积
学过信号处理相关理论的同学一定知道,卷积就是对信号进行如下操作:
( f ∗ g ) ( t ) = ∫ − ∞ ∞ f ( τ ) g ( t − τ ) d τ . (f*g)(t) = \int_{-\infty}^\infty f(\tau)g(t-\tau)d\tau\,. (f∗g)(t)=∫−∞∞f(τ)g(t−τ)dτ.
当然,这是对连续信号,如果信号是离散的,那么就是这样:
( f ∗ g ) ( t ) = ∑ τ = − ∞ ∞ f ( τ ) g ( t − τ ) . (f*g)(t) = \sum_{\tau=-\infty}^\infty f(\tau)g(t-\tau)\,. (f∗g)(t)=τ=−∞∑∞f(τ)g(t−τ).
而在图像处理领域,卷积说白了就是把这个公式拓展到了二维嘛:
( f ∗ g ) ( x , y ) = ∑ n 1 = − ∞ ∞ ∑ n 2 = − ∞ ∞ f ( n 1 , n 2 ) g ( x − n 1 , y − n 2 ) . (f*g)(x,y) = \sum_{n_1=-\infty}^\infty \sum_{n_2=-\infty}^\infty f(n_1,n_2)g(x-n_1,y-n_2)\,. (f∗g)(x,y)=n1=−∞∑∞n2=−∞∑∞f(n1,n2)g(x−n1,y−n2).
其中f就是我们说的卷积核,我们假设卷积核大小为M*N,那么可以认为f函数在除了这个范围后的值为0,那么从负无穷到正无穷的求和就可以变成0到M,0到N的求和,这样,上述式子就变成了我们平常看到的通俗理解卷积,如下图: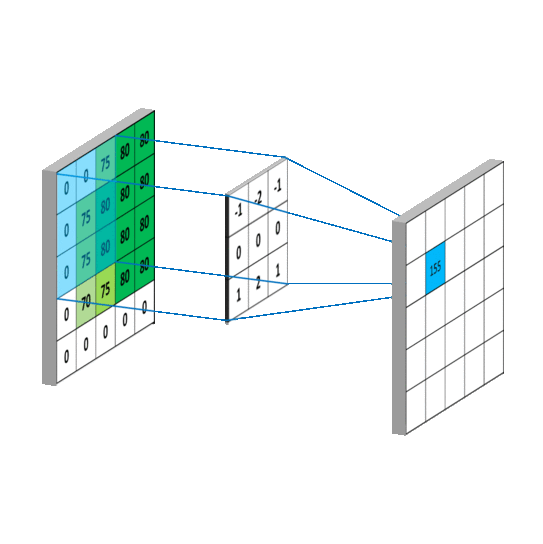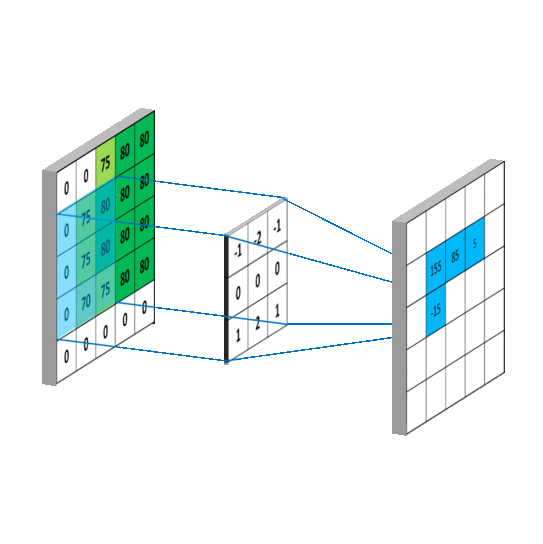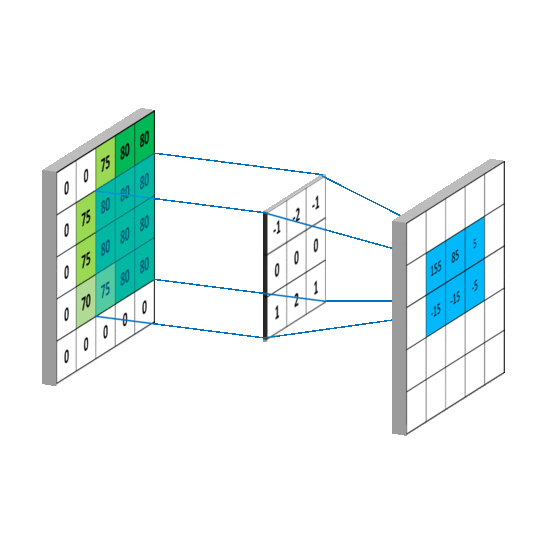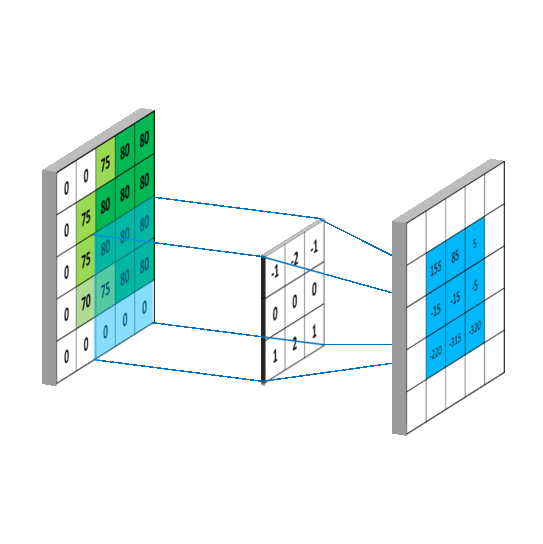
从信号处理的角度来看,卷积计算这么麻烦,有什么用呢?
众所周知,它和傅里叶变换或者拉普拉斯变换有着密切的关系。可以用下面两句绕口令表述:
卷积的傅里叶变换等于傅里叶变换的乘积
乘积的傅里叶变换等于傅里叶变换的卷积
写成公式:
F ( f ∗ g ) = F ( f ) F ( g ) F ( f g ) = F ( f ) ∗ F ( g ) \mathscr{F}(f*g)=\mathscr{F}(f)\mathscr{F}(g)\\ \mathscr{F}(fg)=\mathscr{F}(f)*\mathscr{F}(g) F(f∗g)=F(f)F(g)F(fg)=F(f)∗F(g)
正是由于这样的性质,而卷积可以用于还原信号,所以我们用信号傅里叶变换的乘积再做逆变换来计算卷积,从而能做信号处理里的好多事情。
按照这样的思路,如果我们能够导出图的傅里叶变换,我们就能导出图卷积的公式。
傅里叶变换
信号的傅里叶变换
上面说了这么多,那什么是傅里叶变换呢,这里简要带大家回忆一下,如果不懂的同学就自行百度了
傅里叶变换与逆变换定义如下:
F ( f ) = F ( ω ) = ∫ − ∞ ∞ f ( t ) e − j ω t d t \mathscr{F}(f)=F(\omega)=\int_{-\infty}^\infty f(t)e^{-j\omega t}dt F(f)=F(ω)=∫−∞∞f(t)e−jωtdt
F − 1 ( F ) = f ( t ) = 1 2 π ∫ − ∞ ∞ F ( ω ) e j ω t d ω \mathscr{F}^{-1}(F)=f(t)=\frac{1}{2\pi}\int_{-\infty}^\infty F(\omega)e^{j\omega t}d\omega F−1(F)=f(t)=2π1∫−∞∞F(ω)ejωtdω
傅里叶变换为傅里叶级数的拓展,傅里叶级数为求和的形式,只是对于周期信号适用,而当对于任意信号时,可以认为周期趋于无穷,频谱谱线也就无限靠近形成连续谱,求和也变成了积分的形式。
同样,离散的傅里叶变换变成求和号即可。
从另一个角度看,傅里叶变换可以看做是函数与基函数 e − j ω t e^{-j\omega t} e−jωt的积分,我们研究一下这个基函数。
对其求拉普拉斯,我们可以得到:
Δ e − j ω t = ∂ 2 ∂ t 2 e − j ω t = − ω 2 e − j ω t \Delta e^{-j\omega t}=\frac{\partial^{2}}{\partial t^{2}}e^{-j\omega t}=-\omega^2e^{-j\omega t} Δe−jωt=∂t2∂2e−jωt=−ω2e−jωt
按照特征值的定义:
对于一种变换A,按照线性代数相关知识,其广义特征方程定义为:
A V = λ V AV=\lambda V AV=λV
其中V是特征向量, λ \lambda λ是特征值
可以看出, e − j ω t e^{-j\omega t} e−jωt是拉普拉斯算子的特征函数,而 ω \omega ω与特征值有关。
图的傅里叶变换
按照上一篇博客里证明过的,图的拉普拉斯矩阵其实就是图的拉普拉斯算子,然后套用上面的关系,我们可以得到:
L U = λ U LU=\lambda U LU=λU
仿照上面的傅里叶变换的公式,我们可以导出图上傅里叶变换公式:
F ( λ i ) = f ^ ( λ i ) = ∑ i = 1 N f ( i ) u l ( i ) F(\lambda_i)=\hat f(\lambda_i)=\sum_{i=1}^Nf(i)u_l(i) F(λi)=f^(λi)=i=1∑Nf(i)ul(i)
按照上一篇博客里拉普拉斯矩阵的特征值分解,可以得到矩阵U,其列向量即为特征向量,这里记做 u l u_l ul。
注意,这里是向量点乘形式,这里的u我们看做复数形式,所以在点乘时,要对u取共轭。
上式求得的是节点i的傅里叶变换值。然后我们可以把这个写成矩阵形式:
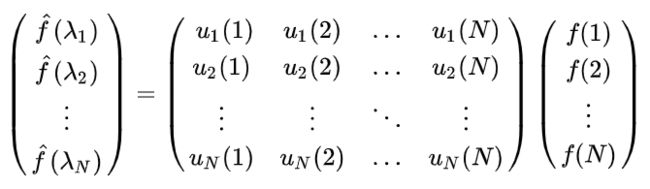
这样我们就得出了图上的傅里叶变换:
f ^ = U T f \hat f=U^Tf f^=UTf
同理,逆变换为:
f ( λ i ) = ∑ l = 1 N f ^ ( i ) u l ( i ) f(\lambda_i)=\sum_{l=1}^N\hat f(i)u_l(i) f(λi)=l=1∑Nf^(i)ul(i)
其他不变,改为对l求和即可。
其矩阵形式为:
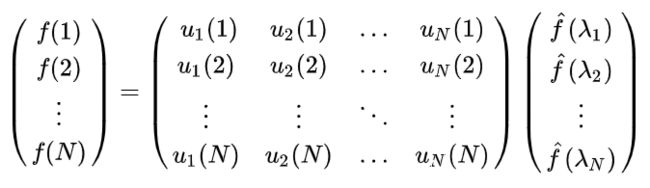
即:
f = U f ^ f=U\hat f f=Uf^
注:这里我们的定义是类比下来的,将原傅里叶变换的基函数 e − j ω t e^{-j\omega t} e−jωt类比为特征向量u,因为他们都和特征值有关。实际上,根据线性代数的知识,可以证明这n个特征向量u是线性空间的一组基,而且是正交基。在傅里叶变换中,变换后的函数自变量变为特征值 ω \omega ω,故在这里,变换后的自变量变为特征值 λ \lambda λ,如下图:

图卷积
根据上面定义,图上的傅里叶变换与逆变换为:
f ^ = U T f f = U f ^ \hat f=U^Tf\\ f=U\hat f f^=UTff=Uf^
根据傅里叶变换与卷积的关系,为了导出图卷积公式,我们计算图与卷积核的傅里叶变换,将其想乘,再求其逆变换:
f ∗ g = F − 1 ( F ( f ) F ( g ) ) f*g=\mathscr{F}^{-1}(\mathscr{F}(f)\mathscr{F}(g)) f∗g=F−1(F(f)F(g))
带入可得:
f ∗ g = U ( ( U T f ) ⊙ ( U T g ) ) f*g=U((U^Tf)\odot(U^Tg)) f∗g=U((UTf)⊙(UTg))
其中 ⊙ \odot ⊙为哈达马积,即两向量对应元素相乘。
这里对于卷积核的傅里叶变换我们可以写为:
U T g = ( g ^ ( λ 1 ) , g ^ ( λ 2 ) , . . . , g ^ ( λ n ) ) T U^Tg=(\hat g(\lambda_1),\hat g(\lambda_2),...,\hat g(\lambda_n))^T UTg=(g^(λ1),g^(λ2),...,g^(λn))T
故可将别扭的哈达马积去掉,写成:
f ∗ g = U d i a g ( g ^ ( λ 1 ) , g ^ ( λ 2 ) , . . . , g ^ ( λ n ) ) U T f f*g=Udiag(\hat g(\lambda_1),\hat g(\lambda_2),...,\hat g(\lambda_n))U^Tf f∗g=Udiag(g^(λ1),g^(λ2),...,g^(λn))UTf
GCN(图卷积神经网络)
将图卷积相关理论构成神经网络即图卷积神经网络(Graph Convolutional Network)。
在上一篇博客里我们定义了图卷积层的三种形式,这里我们具体地将我们导出的图卷积公式带入。
第一代GCN
在第一代GCN中,作者直接将卷积核的傅里叶变换 d i a g ( g ^ ( λ l ) ) diag(\hat g(\lambda_l)) diag(g^(λl))设定为可学习的卷积核 d i a g ( θ l ) diag(\theta_l) diag(θl),卷积层就变成了下面这个样子:
y o u t p u t = σ ( U g θ ( Λ ) U T x ) y_{output}=\sigma(Ug_\theta(\Lambda)U^Tx) youtput=σ(Ugθ(Λ)UTx)
其中 g θ ( Λ ) = d i a g ( θ l ) g_\theta(\Lambda)=diag(\theta_l) gθ(Λ)=diag(θl)即为卷积核
其实,同时对于大型图,可能有上亿个节点,这样卷积核就需要学习上亿个参数。
第二代GCN
为了避免上述的问题,第二代GCN将 d i a g ( g ^ ( λ l ) ) diag(\hat g(\lambda_l)) diag(g^(λl))设定成 d i a g ( ∑ j = 0 k α j λ l j ) diag(\sum_{j=0}^k\alpha_j\lambda_l^j) diag(∑j=0kαjλlj),即把傅里叶变换 g ^ ( λ l ) \hat g(\lambda_l) g^(λl)设置为一个自变量为 λ l \lambda_l λl的幂级数,最高次为k。那么参数量就变成了k个,即 α \alpha α。
而按照之前的推导对于拉普拉斯矩阵有性质:
L 2 = U Λ U T U Λ U T = U Λ 2 U T L n = U Λ n U T L^2=U\Lambda U^TU\Lambda U^T=U\Lambda^2 U^T\\ L^n=U\Lambda^n U^T L2=UΛUTUΛUT=UΛ2UTLn=UΛnUT
这样就可以有以下化简:
U ∑ j = 0 k α j Λ j U T = ∑ j = 0 k α j U Λ j U T = ∑ j = 0 k α j L j U\sum_{j=0}^k\alpha_j\Lambda^jU^T=\sum_{j=0}^k\alpha_jU\Lambda^jU^T=\sum_{j=0}^k\alpha_jL^j Uj=0∑kαjΛjUT=j=0∑kαjUΛjUT=j=0∑kαjLj
那么图卷积层就表示为:
y o u t p u t = σ ( ∑ j = 0 K − 1 α j L j x ) y_{output}=\sigma(\sum_{j=0}^{K-1} \alpha_jL^jx) youtput=σ(j=0∑K−1αjLjx)
这个方法太巧妙了,其实就是通过权值共享把要学习的参数量变成幂级数的系数。原来我有几个节点,就得有几个参数,现在我们只需要k个系数就能进行学习。
总结
这篇文章介绍了图卷积的推导以及GCN网络的构建。在最后,把需要学习的参数降为为k个幂级数的系数。在后来的研究中,研究人员也提出很多种不同的GCN,仅目前pytorch集成的就不下20种了:
pytorch geometric的github:https://github.com/rusty1s/pytorch_geometric
其中改进方法大多为对上述幂级数的改进,可以换成其他函数生成方式,或插值方式。如:贝塞尔曲线、B-样条曲线等。
目前,通过B-样条曲线的方法构建的GCN效果很好,该方法来自CVPR2018的论文SplineCNN: Fast Geometric Deep Learning with Continuous B-Spline Kernels。
但也不能说其他的方法效果一定不好,目前这方面还在研究中,这些图卷积的方法效果也基本都差不多,在实际应用中通常要经过多次的尝试找到效果最好的一种。