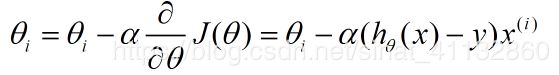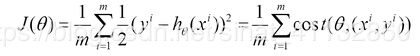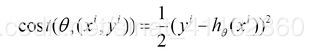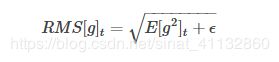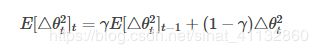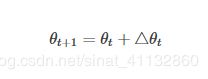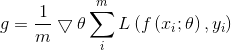机器学习之优化方法

机器学习中，有许多优化器，下面分析常用的。

优化方法的作用，是通过进行某种方式的训练，来最小化(或最大化)损失函数loss(x)。

目录

gradient descent梯度下降

Stochastic Gradient Descent随机梯度下降

Mini-batch Gradient Descent小批量梯度下降

Momentum动量技术

Nesterov  Momentum    Nesterov梯度加速法

AdaGrad

Adadelta

RMSProp

Adaptive Moment Estimation自适应时刻估计方法

如何选择优化方法

---

gradient descent梯度下降

梯度下降是神经网络中最常用的求极值点的方法。

梯度下降法，就是利用负梯度方向来决定每次迭代的新的搜索方向，使得每次迭代能使待优化的目标函数逐步减小。

梯度下降法是2范数下的最速下降法。 最速下降法的一种简单形式是：x(k+1)=x(k)-a*g(k),其中a称为学习速率，可以是较小的常数。g（k）是x(k)的梯度。梯度就是函数的偏导数。

假设损失函数为线性回归中的平方损失函数

                           

对参数求偏导，

                           

更新参数的过程，就是θi会向着梯度最小的方向进行减少。θi表示更新之前的值，-后面的部分表示按梯度方向减少的量，α表示步长，也就是每次按照梯度减少的方向变化多少。

                        

换言之，如果是神经网络，那么求w，b等参数也是同样的方法。这么理解是没问题的，直观上也是可以解释可以优化损失函数的

但是梯度下降法处理一些复杂的非线性函数会出现问题，如Rosenbrock函数：

,其最小值在处，函数值为。但是此函数具有狭窄弯曲的山谷，最小点

就在这些山谷之中，并且谷底很平。优化过程是之字形的向极小值点靠近，速度非常缓慢

优点 

1全局最优解；

2易于并行实现

缺点：

1靠近极小值时收敛速度减慢。

2直线搜索时可能会产生一些问题。

3可能会“之字形”地下降。

批量梯度下降法（Batch Gradient Descent，简称BGD）是梯度下降法最原始的形式，它的具体思路是在更新每一参数时都使用所有的样本来进行更新，与上面的形式一致，不再赘述

Stochastic Gradient Descent随机梯度下降

批量梯度下降法在更新每一个参数时，需要所有的训练样本，训练过程会随着样本数量的加大而变得非常缓慢。

随机梯度下降法是为了这个问题提出的

                            

代价函数为

                               

每次更新参数时，随机选取一个样本点来更新

                            θ=θ−η⋅∇θJ(θ;xi;yi)

随机梯度下降算法每次只随机选择一个样本来更新模型参数，因此每次的学习是非常快速的，并且可以进行在线更新。

随机梯度下降最大的缺点在于每次更新可能并不会按照正确的方向进行，因此可以带来优化波动，因为是随机选取的，那么在解的空间搜索最优点比较盲目，但是最终会到达一个局部最优点，甚至全局最优点。但是更次的次数会变得很多

优点：训练速度快（每次只更新一个样本）

缺点：准确度下降，（因为并不是全局最优点），很难并行实现

Mini-batch Gradient Descent小批量梯度下降

小批量梯度下降考虑了批量梯度下降和随机梯度下降结合的方法，在更新速度和更新次数中保持了一个平衡，即每次更新时在样本中选取m个样本，m

                        θ=θ−η⋅∇θJ(θ;xi:i+m;yi:i+m)

伪代码：
 

对每轮训练：

     将数据打乱

     对每个数据（在抽取到的m个数据中）：

                 计算梯度，更新参数

 

梯度下降算法的效果较好，在神经网络中已经广泛使用，但存在一些问题，学习速率的选择，一种解决办法是

             随时观察值，如果cost function变小了，那么继续训练，如果代价函数值没变或者变大，则需要选择更小的值

Momentum动量技术

定义  通过优化相关方向的训练和弱化无关方向的振荡，来加速SGD训练。

动量在参数更新中加上上一次的更新量，即动量项。

                                                 V(t)=γV(t−1)+η∇(θ).J(θ)

                                                     θ=θ−V(t)

与SGD相比，在更新参数theta时，除了像SGD一样按照本次的反向梯度更新外，还会：

将上次更新的反向梯度乘以系数alpha后也更新到参数theta中。动量项γ通常设定为0.9，或相近的某个值。

Nesterov  Momentum    Nesterov梯度加速法

      先根据之前的动量进行大步跳跃，然后计算梯度进行校正，从而实现参数更新。这种预更新方法能防止大幅振荡，不会错过最小值，并对参数更新更加敏感

                           V(t)=γV(t−1)+η∇(θ)J( θ−γV(t−1) )

                             θ=θ−V(t)

该优化器相对于Momentum，唯一不同的是计算反向梯度的时机。Momentum计算的是当前位置的反向梯度，Nesterov Momentum 计算的是按照上次更新方向走一小步后的反向梯度

AdaGrad

Adagrad方法是通过参数来调整合适的学习率η，对稀疏参数进行大幅更新和对频繁参数进行小幅更新。因此，Adagrad方法非常适合处理稀疏数据

AdaGrad的基本思想是对每个变量用不同的学习率，这个学习率在一开始比较大，用于快速梯度下降。随着优化过程的进行，对于已经下降很多的变量，则减缓学习率，对于还没怎么下降的变量，则保持一个较大的学习率

用(xt)i表示第i个变量xi在第t次迭代时的值，(▽f(xt))i表示函数在t次迭代时，对第i个变量xi的梯度值，则算法更新梯度的公式如下：

                         

AdaGrad非常适合样本稀疏的问题，稀疏的样本下，每次梯度下降的方向，以及涉及的变量都可能有很大的差异。AdaGrad的缺点是虽然不同变量有了各自的学习率，但是初始的全局学习率还是需要手工指定。如果全局学习率过大，优化同样不稳定；而如果全局学习率过小，因为AdaGrad的特性，随着优化的进行，学习率会越来越小，很可能还没有到极值就停滞不前了。

优点：

不需要手工来调整学习率。

缺点：

学习率η总是在降低和衰减。其需要手工设置一个全局的初始学习率。

deeplearning一书中给出的伪代码如下：

Adadelta

为了避免上述Adagrad中学习率单调下降的问题，adadelta算法产生，Adadelta限制把历史梯度累积窗口限制到固定的尺寸w的梯度平方和，而不是累加所有的梯度平方和。即使用附加动量法的思想去替代上述E[gt−w:t]以及E[g2t−w:t]中w次的记录

定义 动态平均值[g2]t

                       

为取决于当前梯度值和上一刻梯度的平均值   

求平方根，下面记为RMS[g]t

                            

ϵ为常数，目的是为了防止第一次迭代Δx为0,以及之前的参数更新过小。现在用E[g2]t简单代替原来的AdaGrad中

的对角矩阵Gt:（上面叙述的adagrad中的分母部分）

                             

定义指数衰减均值，代替梯度平方，二用参数平方来更新

                            

RMS[△θ]t−1代替学习率η，得到更新规则：

                                     

                                

优点：不需要设置学习率

缺点：可能达到局部最优解

RMSProp

RMSprop 和 Adadelta 都是为了解决 Adagrad 学习率急剧下降问题的，在神经网络为非凸的条件下，效果更好

更新规则如下

 

《deeplearning》中的伪代码：

                 

对比adagrad算法，只有倒数第四行有改动。算法中的p一般取0.9

越早时候计算的梯度对计算衰减系数的影响越小，这种影响的减小速度就是decay_rate的指数衰减速度

Adaptive Moment Estimation自适应时刻估计方法

Adam综合了Momentum的更新方向策略和RMProp的计算衰减系数策略

 

 

一般设为0.9，decay_rate一般设为0.99，一般设为10-6

伪代码如下

                         

 

如何选择优化方法

如果数据是稀疏的，就用自适用方法，即 Adagrad, Adadelta, RMSprop, Adam。

RMSprop, Adadelta, Adam 在很多情况下的效果是相似的。

Adam 就是在 RMSprop 的基础上加了 bias-correction 和 momentum，

随着梯度变的稀疏，Adam 比 RMSprop 效果会好。

整体来讲，Adam 是最好的选择。

参考 https://baike.baidu.com/item/%E6%A2%AF%E5%BA%A6%E4%B8%8B%E9%99%8D/4864937?fr=aladdin

       https://blog.csdn.net/wangliang0633/article/details/79082901

      http://book.51cto.com/art/201710/555102.htm

     https://www.cnblogs.com/guoyaohua/p/8542554.html