滑动窗口法详解

算法目的

该算法展示了如何将嵌套for循环在少数问题中转换为单个for循环，从而减少了时间的复杂性。

前言

一个经典的问题

给一组大小为n的整数数组，计算长度为k的子数组的最大值
我们希望的结果如下

Input  : arr[] = {100, 200, 300, 400}
         k = 2
Output : 700

Input  : arr[] = {1, 4, 2, 10, 23, 3, 1, 0, 20}
         k = 4 
Output : 39
We get maximum sum by adding subarray {4, 2, 10, 23}
of size 4.

Input  : arr[] = {2, 3}
         k = 3
Output : Invalid
There is no subarray of size 3 as size of whole
array is 2.

该技术可以通过总线上的窗格得到最好的理解，考虑长度为n的窗口和长度为k的窗格。考虑一下，最初窗格处于极端的左边，即从左边开始的0个单位。现在，将窗口与大小为n和平面的数组arr []以k大小的元素的current_sum相关联。现在，如果我们在窗户上施加力量，使其向前移动一个单位距离。该窗格将覆盖下一个k个连续元素。

考虑数组arr [] = { 5,2，-1,0,3 }，k = 3和n = 5的值

应用滑动窗口技术：

1. 我们使用线性循环计算n个项中前k个元素的总和，并将总和存储在变量window_sum中。
2. 然后，我们将在阵列上线性滑动直至达到最终并同时追踪最大和。
3. 要获得k个元素块的当前总和，只需从前一个块中减去第一个元素并添加当前块的最后一个元素即可。 下面的表示将清楚说明窗口如何在阵列上滑动。

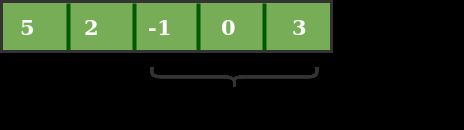
这是我们计算从索引0开始的初始窗口总和的初始阶段。在这个阶段，窗口和为6.现在，我们将maximum_sum设置为current_window，即6。

现在，我们用单位索引来滑动我们的窗口。因此，现在它从窗口中丢弃5并将0添加到窗口。因此，我们将得到新的窗口总和，减去5，然后加上0。所以，我们的窗口和现在变成1.现在，我们将比较这个窗口和与maximum_sum。因为它更小，我们不会改变maximum_sum。

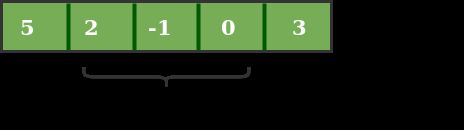
同样，现在我们再次用一个单位索引来滑动我们的窗口，并获得新的窗口总和为2.我们再一次检查这个当前窗口总和是否大于maximum_sum，直到现在。有一次，它再小一些，所以我们不改变maximum_sum。

因此，对于上面的数组，我们的maximum_sum是6。

代码如下

#include 

using namespace std;

int maxSum(int arr[], int n, int k)
{
    if (n < k)
    {
        cout << "Invaild";
        return -1;
    }
    int max_sum = 0;
    for (int i=0; i

总结

现在，很明显时间复杂性是线性的，因为我们可以看到只有一个循环运行在我们的代码中。因此，我们的时间复杂度是O（n）。
我们可以使用这种技术来查找最大/最小k-子阵列，XOR，乘积，总和等

如果你觉得还不错可以右侧点个赞幺，谢谢

#参考资料
geekforgeeks 滑动窗口法详解
https://www.geeksforgeeks.org/window-sliding-technique/

geekforgeeks 经典类型题
https://www.geeksforgeeks.org/tag/sliding-window/

leetcode的经典模板