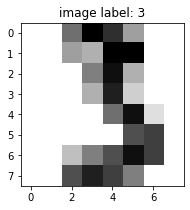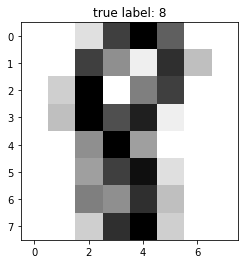3_基于numpy的mlp反向传播实现
文章目录
- 基于Numpy的反向传播
- a) Logitstic regression
- 对标签进行one-hot编码(类似keras中的to_categorical)
- Softmax
- 实现交叉熵,也就是negative log likelihoot
- b)多层感知机
- c) 更多操作
- 查找预测结果最差的样本
- 超参数设置
对于深度学习反向传播的推导主要有三部分第一部分交叉熵求导,第二部分softmax函数的求导,第三部分f(wx+b)的求导,后期会把这部分理论内容写到博客中。不写的博客中总是推了忘又推又忘的节奏。
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import load_digits
digits = load_digits()
sample_index = 45
plt.figure(figsize=(3, 3))
plt.imshow(digits.images[sample_index], cmap=plt.cm.gray_r,
interpolation='nearest')
plt.title("image label: %d" % digits.target[sample_index]);
对数据进行标准化处理
from sklearn import preprocessing
from sklearn.model_selection import train_test_split
data = np.asarray(digits.data, dtype='float32')
target = np.asarray(digits.target, dtype='int32')
X_train, X_test, y_train, y_test = train_test_split(
data, target, test_size=0.15, random_state=37)
# mean = 0 ; standard deviation = 1.0
scaler = preprocessing.StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)
# print(scaler.mean_)
# print(scaler.scale_)
X_train.shape
(1527, 64)
X_train.dtype
dtype('float32')
X_test.shape
(270, 64)
y_train.shape
(1527,)
y_train.dtype
dtype('int32')
基于Numpy的反向传播
a) Logitstic regression
这部分将用Numpy实现logistic regression,并完成SGD的反向传播,具体有:
- 实现无隐藏层的前向运算网络,实际也就是一个logitstic regression
y = s o f t m a x ( W x ˙ + b ) y = softmax(\mathbf{W} \dot x + b) y=softmax(Wx˙+b) - 构建一个分类函数,输入 x x x时,将最大分类的概率值返回
- 构建一个损失函数,能够处理批量输入 X X X还有对应标签 y t r u e y_{true} ytrue
- 构建求梯度的函数 d W − log ( s o f t m a x ( W x ˙ + b ) ) \frac{d}{W}-\log(softmax(W\dot{x}+b)) Wd−log(softmax(Wx˙+b)),并验证梯度的有效性
- 构建对参数 W \mathbf{W} W和 b \mathbf{b} b的梯度更新函数
对标签进行one-hot编码(类似keras中的to_categorical)
import numpy as np
def one_hot(n_classes,y):
return np.eye(n_classes)[y]
one_hot(10,3)
array([0., 0., 0., 1., 0., 0., 0., 0., 0., 0.])
one_hot(10,[0,4,9])
array([[1., 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 1., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0., 1.]])
Softmax
s o f t m a x ( x ) = 1 ∑ i = 1 n e x i ⋅ [ e x 1 e x 2 ⋮ e x n ] softmax(\mathbf{x})= \frac{1}{\sum_{i=1}^{n}{e^{x_i}}} \cdot \begin{bmatrix} e^{x_1}\\\\ e^{x_2}\\\\ \vdots\\\\ e^{x_n} \end{bmatrix} softmax(x)=∑i=1nexi1⋅⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡ex1ex2⋮exn⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤
def softmax(X):
"""
这种定义方法可以同时处理向量和矩阵
"""
exp = np.exp(X)
return exp/np.sum(exp,axis=-1,keepdims=True)
print("softmax of a single vector:")
print(softmax([10, 2, -3]))
print(np.sum(softmax([10, 2, -3])))
print("sotfmax of 2 vectors:")
X = np.array([[10, 2, -3],
[-1, 5, -20]])
print(softmax(X))
print(np.sum(softmax(X), axis=1))
softmax of a single vector:
[9.99662391e-01 3.35349373e-04 2.25956630e-06]
1.0
sotfmax of 2 vectors:
[[9.99662391e-01 3.35349373e-04 2.25956630e-06]
[2.47262316e-03 9.97527377e-01 1.38536042e-11]]
[1. 1.]
实现交叉熵,也就是negative log likelihoot
要求要能同时处理向量和矩阵
l o g l i k e l i h o o d = − ∑ i = 1 n y t r u e i ⋅ l o g ( y p r e d i ) loglikelihood=-\sum_{i=1}^{n}{{y_{true}^{i}} \cdot log({y_{pred}^{i}}}) loglikelihood=−∑i=1nytruei⋅log(ypredi)
给定one-hot和Y_true和预测的Y_pred返回似然值
EPSILON=1e-8
def nll(Y_true,Y_pred):
Y_true=np.atleast_2d(Y_true)
Y_pred=np.atleast_2d(Y_pred)
loglikelihoods = np.sum(np.log(EPSILON + Y_pred) * Y_true, axis=-1)
return -np.mean(loglikelihoods)
# Make sure that it works for a simple sample at a time
print(nll([1, 0, 0], [.99, 0.01, 0]))
0.01005032575249135
#如果对错误分类非常高的信任
print(nll([1, 0, 0], [0.01, 0.01, 0.98]))
4.605169185988592
#多个输入输出时的平均结果,估算应该接0
Y_true = np.array([[0, 1, 0],
[1, 0, 0],
[0, 0, 1]])
Y_pred = np.array([[0, 1, 0],
[.99, 0.01, 0],
[0, 0, 1]])
print(nll(Y_true, Y_pred))
0.0033501019174971905
接着,通过SGD来学习一个简单的线性模型,一次处理一个样本one sample each time
class LogisticRegression():
def __init__(self, input_size, output_size):
self.W = np.random.uniform(size=(input_size, output_size),
high=0.1, low=-0.1)
self.b = np.random.uniform(size=output_size,
high=0.1, low=-0.1)
self.output_size = output_size
def forward(self, X):
Z = np.dot(X, self.W) + self.b
return softmax(Z)
def predict(self, X):
if len(X.shape) == 1:
return np.argmax(self.forward(X))
else:
return np.argmax(self.forward(X), axis=1)
def grad_loss(self, x, y_true):
y_pred = self.forward(x)
dnll_output = y_pred - one_hot(self.output_size, y_true)
grad_W = np.outer(x, dnll_output)
grad_b = dnll_output
grads = {"W": grad_W, "b": grad_b}
return grads
def train(self, x, y, learning_rate):
# Traditional SGD update without momentum
grads = self.grad_loss(x, y)
self.W = self.W - learning_rate * grads["W"]
self.b = self.b - learning_rate * grads["b"]
def loss(self, X, y):
return nll(one_hot(self.output_size, y), self.forward(X))
def accuracy(self, X, y):
y_preds = np.argmax(self.forward(X), axis=1)
return np.mean(y_preds == y)
# 构建模型并进行前向推理
n_features = X_train.shape[1]
n_classes = len(np.unique(y_train))
lr = LogisticRegression(n_features, n_classes)
print("Evaluation of the untrained model:")
train_loss = lr.loss(X_train, y_train)
train_acc = lr.accuracy(X_train, y_train)
test_acc = lr.accuracy(X_test, y_test)
print("train loss: %0.4f, train acc: %0.3f, test acc: %0.3f"
% (train_loss, train_acc, test_acc))
Evaluation of the untrained model:
train loss: 2.4864, train acc: 0.080, test acc: 0.063
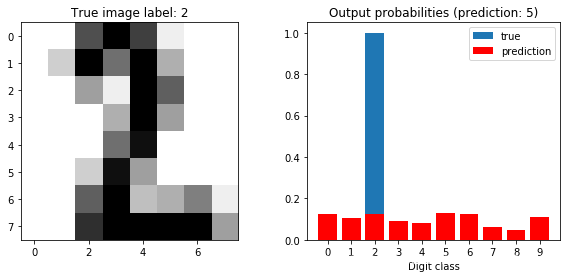
评估随机初始化参数的模型对一个样本的预测情况
def plot_prediction(model, sample_idx=0, classes=range(10)):
fig, (ax0, ax1) = plt.subplots(nrows=1, ncols=2, figsize=(10, 4))
ax0.imshow(scaler.inverse_transform(X_test[sample_idx]).reshape(8, 8), cmap=plt.cm.gray_r,
interpolation='nearest')
ax0.set_title("True image label: %d" % y_test[sample_idx]);
ax1.bar(classes, one_hot(len(classes), y_test[sample_idx]), label='true')
ax1.bar(classes, model.forward(X_test[sample_idx]), label='prediction', color="red")
ax1.set_xticks(classes)
prediction = model.predict(X_test[sample_idx])
ax1.set_title('Output probabilities (prediction: %d)'
% prediction)
ax1.set_xlabel('Digit class')
ax1.legend()
plot_prediction(lr, sample_idx=0)
# 对模型训练一个epoch,Training for one epoch
learning_rate = 0.01
for i, (x, y) in enumerate(zip(X_train, y_train)):
lr.train(x, y, learning_rate)
if i % 100 == 0:
train_loss = lr.loss(X_train, y_train)
train_acc = lr.accuracy(X_train, y_train)
test_acc = lr.accuracy(X_test, y_test)
print("Update #%d, train loss: %0.4f, train acc: %0.3f, test acc: %0.3f"
% (i, train_loss, train_acc, test_acc))
Update #0, train loss: 2.4535, train acc: 0.087, test acc: 0.074
Update #100, train loss: 1.3819, train acc: 0.626, test acc: 0.685
Update #200, train loss: 0.9100, train acc: 0.826, test acc: 0.848
Update #300, train loss: 0.6685, train acc: 0.882, test acc: 0.904
Update #400, train loss: 0.5509, train acc: 0.898, test acc: 0.911
Update #500, train loss: 0.4755, train acc: 0.911, test acc: 0.930
Update #600, train loss: 0.4149, train acc: 0.920, test acc: 0.930
Update #700, train loss: 0.3751, train acc: 0.927, test acc: 0.952
Update #800, train loss: 0.3526, train acc: 0.929, test acc: 0.944
Update #900, train loss: 0.3267, train acc: 0.935, test acc: 0.948
Update #1000, train loss: 0.3055, train acc: 0.938, test acc: 0.956
Update #1100, train loss: 0.2861, train acc: 0.946, test acc: 0.956
Update #1200, train loss: 0.2744, train acc: 0.948, test acc: 0.959
Update #1300, train loss: 0.2620, train acc: 0.950, test acc: 0.944
Update #1400, train loss: 0.2486, train acc: 0.953, test acc: 0.952
Update #1500, train loss: 0.2374, train acc: 0.953, test acc: 0.948
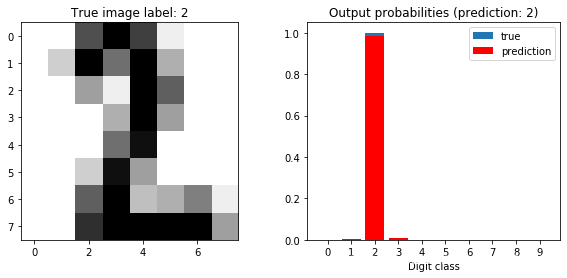
再次对模型进行评估
plot_prediction(lr, sample_idx=0)
b)多层感知机
这个环节要实现只有一个隐藏层的感知机,具休的:
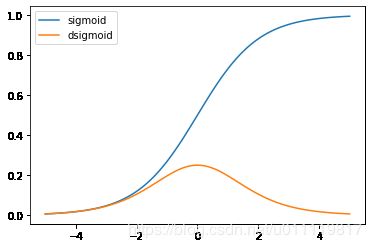
- 实现针对单个元素的
sigmoid函数以及导数dsigmoid
s i g m o i d ( x ) = 1 1 + e − x sigmoid(x)=\frac{1}{1+e^{-x}} sigmoid(x)=1+e−x1
d s i g m o i d ( x ) = s i g m o i d ( x ) ⋅ ( 1 − s i g m o i d ( x ) ) dsigmoid(x)=sigmoid(x) \cdot (1-sigmoid(x)) dsigmoid(x)=sigmoid(x)⋅(1−sigmoid(x))
def sigmoid(X):
return 1 / (1 + np.exp(-X))
def dsigmoid(X):
sig=sigmoid(X)
return sig * (1 - sig)
x = np.linspace(-5, 5, 100)
plt.plot(x, sigmoid(x), label='sigmoid')
plt.plot(x, dsigmoid(x), label='dsigmoid')
plt.legend(loc='best');
定义模型:
- h = s i g m o i d ( W h x + b h ) \mathbf{h}=sigmoid(\mathbf{W}^h\mathbf{x}+\mathbf{b}^h) h=sigmoid(Whx+bh)
- y = s i g m o i d ( W 0 x + b o ) \mathbf{y}=sigmoid(\mathbf{W}^0\mathbf{x}+\mathbf{b}^o) y=sigmoid(W0x+bo)
- 注意:
- 代码要简捷
forward前向运算多了一层针对element的运算
- 计算所有变量的梯度并更新
- 实现
train和loss函数
EPSILON=1e-8
class NeuralNet():
"""只有一层隐藏的MLP"""
def __init__(self,input_size,hidden_size,output_size):
self.W_h=np.random.uniform(size=(input_size,hidden_size),high=0.01,low=-0.01)
self.b_h=np.zeros(hidden_size)
self.W_o = np.random.uniform(size=(hidden_size, output_size), high=0.01, low=-0.01)
self.b_o = np.zeros(output_size)
self.output_size = output_size
def forward(self,X,keep_activations=False):
z_h=np.dot(X,self.W_h)+self.b_h
h = sigmoid(z_h)
z_o = np.dot(h, self.W_o) + self.b_o
y = softmax(z_o)
if keep_activations:
return y, h, z_h
else:
return y
def loss(self, X, y):
return nll(one_hot(self.output_size, y), self.forward(X))
def grad_loss(self, x, y_true):
y, h, z_h = self.forward(x, keep_activations=True)
grad_z_o = y - one_hot(self.output_size, y_true)
grad_W_o = np.outer(h, grad_z_o)
grad_b_o = grad_z_o
grad_h = np.dot(grad_z_o, np.transpose(self.W_o))
grad_z_h = grad_h * dsigmoid(z_h)
grad_W_h = np.outer(x, grad_z_h)
grad_b_h = grad_z_h
grads = {"W_h": grad_W_h, "b_h": grad_b_h,
"W_o": grad_W_o, "b_o": grad_b_o}
return grads
def train(self, x, y, learning_rate):
# Traditional SGD update on one sample at a time
grads = self.grad_loss(x, y)
self.W_h = self.W_h - learning_rate * grads["W_h"]
self.b_h = self.b_h - learning_rate * grads["b_h"]
self.W_o = self.W_o - learning_rate * grads["W_o"]
self.b_o = self.b_o - learning_rate * grads["b_o"]
def predict(self, X):
if len(X.shape) == 1:
return np.argmax(self.forward(X))
else:
return np.argmax(self.forward(X), axis=1)
def accuracy(self, X, y):
y_preds = np.argmax(self.forward(X), axis=1)
return np.mean(y_preds == y)
n_hidden = 10
model = NeuralNet(n_features, n_hidden, n_classes)
model.loss(X_train, y_train)
2.3026371675800914
model.accuracy(X_train, y_train)
0.10019646365422397
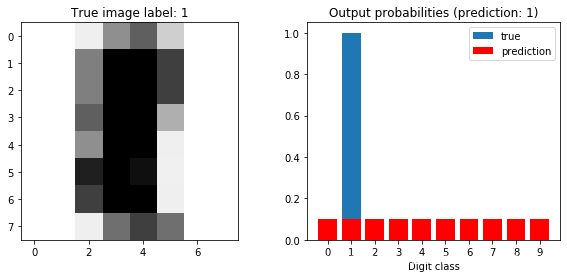
plot_prediction(model, sample_idx=5)
losses, accuracies, accuracies_test = [], [], []
losses.append(model.loss(X_train, y_train))
accuracies.append(model.accuracy(X_train, y_train))
accuracies_test.append(model.accuracy(X_test, y_test))
print("Random init: train loss: %0.5f, train acc: %0.3f, test acc: %0.3f"
% (losses[-1], accuracies[-1], accuracies_test[-1]))
for epoch in range(15):
for i, (x, y) in enumerate(zip(X_train, y_train)):
model.train(x, y, 0.1)
losses.append(model.loss(X_train, y_train))
accuracies.append(model.accuracy(X_train, y_train))
accuracies_test.append(model.accuracy(X_test, y_test))
print("Epoch #%d, train loss: %0.5f, train acc: %0.3f, test acc: %0.3f"
% (epoch + 1, losses[-1], accuracies[-1], accuracies_test[-1]))
Random init: train loss: 2.30264, train acc: 0.100, test acc: 0.107
Epoch #1, train loss: 0.38531, train acc: 0.903, test acc: 0.870
Epoch #2, train loss: 0.16841, train acc: 0.966, test acc: 0.937
Epoch #3, train loss: 0.10853, train acc: 0.978, test acc: 0.941
Epoch #4, train loss: 0.08321, train acc: 0.983, test acc: 0.944
Epoch #5, train loss: 0.07334, train acc: 0.984, test acc: 0.952
Epoch #6, train loss: 0.05982, train acc: 0.988, test acc: 0.952
Epoch #7, train loss: 0.04968, train acc: 0.993, test acc: 0.952
Epoch #8, train loss: 0.04381, train acc: 0.993, test acc: 0.948
Epoch #9, train loss: 0.03836, train acc: 0.996, test acc: 0.948
Epoch #10, train loss: 0.03343, train acc: 0.997, test acc: 0.963
Epoch #11, train loss: 0.02923, train acc: 0.999, test acc: 0.963
Epoch #12, train loss: 0.02605, train acc: 0.999, test acc: 0.959
Epoch #13, train loss: 0.02334, train acc: 0.999, test acc: 0.959
Epoch #14, train loss: 0.02100, train acc: 0.999, test acc: 0.959
Epoch #15, train loss: 0.01895, train acc: 0.999, test acc: 0.959
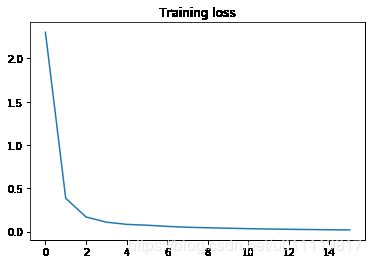
plt.plot(losses)
plt.title("Training loss");
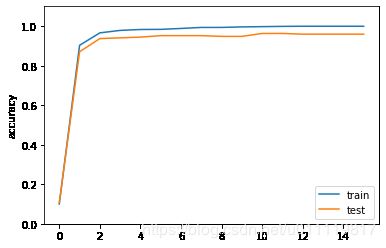
plt.plot(accuracies, label='train')
plt.plot(accuracies_test, label='test')
plt.ylim(0, 1.1)
plt.ylabel("accuracy")
plt.legend(loc='best');
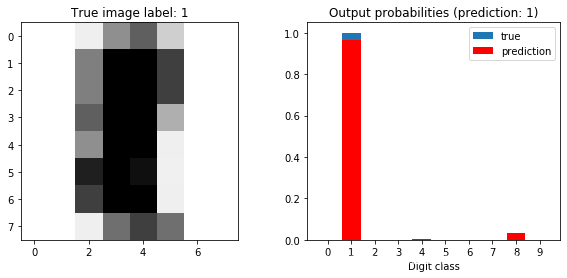
plot_prediction(model, sample_idx=5)
c) 更多操作
查找预测结果最差的样本
- 找到预测结果最差的样本
- 使用
plot_predictions查看
test_losses = -np.sum(np.log(EPSILON + model.forward(X_test))
* one_hot(10, y_test), axis=1)
#按loss从小到大排序,前边的loss小,后边的loss大
ranked_by_loss = test_losses.argsort()
#显示最差的5个样本
worst_idx = ranked_by_loss[-5:]
print("test losses:", test_losses[worst_idx])
for idx in worst_idx:
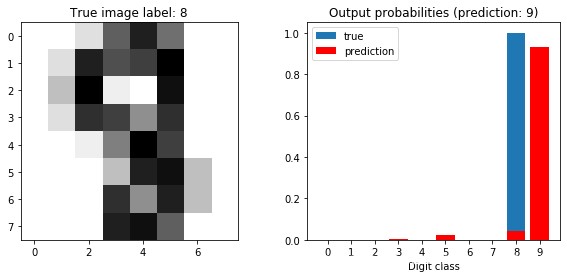
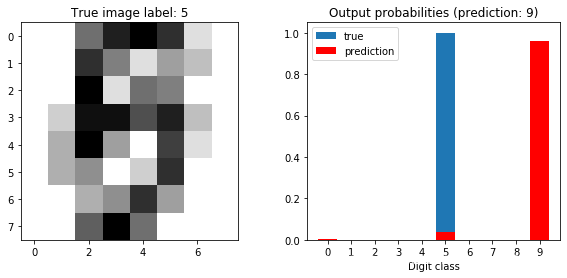
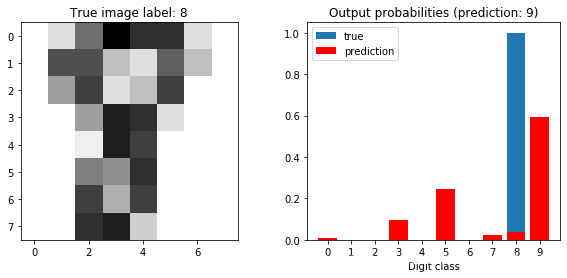
plot_prediction(model, sample_idx=idx)
test losses: [3.15997934 3.33671786 3.34218763 4.99581726 8.59161317]
超参数设置
- 改变超参数可以做很多不同的实验:
- 学习率
- 隐藏层节点个数
- 参数初始化方法:全零,均匀分布,正态分存等
- 激活函数的选用
- 加另外一个
- 梯度下降法的:Momentum
- 回到keras:
- 用keras实现相同的网络
- 相同参数情况下,keras和numpy实现应该是相同效果
- 计算第42个样本的 negative log likelihood
- 计算所有测试样的平均负对数似然值
- 计算所有训练样本的 negative log likelihood
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
from tensorflow.keras.optimizers import SGD
from tensorflow.keras.utils import to_categorical
n_features = 8 * 8
n_classes = 10
n_hidden = 10
keras_model = Sequential()
keras_model.add(Dense(n_hidden, input_dim=n_features, activation='sigmoid'))
keras_model.add(Dense(n_classes, activation='softmax'))
keras_model.compile(optimizer=SGD(lr=3),
loss='categorical_crossentropy', metrics=['accuracy'])
keras_model.fit(X_train, to_categorical(y_train), epochs=15, batch_size=32);
Train on 1527 samples
Epoch 1/15
1527/1527 [==============================] - 1s 901us/sample - loss: 0.7866 - accuracy: 0.7865
Epoch 2/15
1527/1527 [==============================] - 0s 101us/sample - loss: 0.2057 - accuracy: 0.9548
Epoch 3/15
1527/1527 [==============================] - 0s 101us/sample - loss: 0.1388 - accuracy: 0.9692
Epoch 4/15
1527/1527 [==============================] - 0s 94us/sample - loss: 0.0945 - accuracy: 0.9797
Epoch 5/15
1527/1527 [==============================] - 0s 101us/sample - loss: 0.0801 - accuracy: 0.9830
Epoch 6/15
1527/1527 [==============================] - 0s 94us/sample - loss: 0.0670 - accuracy: 0.9876
Epoch 7/15
1527/1527 [==============================] - 0s 92us/sample - loss: 0.0555 - accuracy: 0.9895
Epoch 8/15
1527/1527 [==============================] - 0s 98us/sample - loss: 0.0494 - accuracy: 0.9902
Epoch 9/15
1527/1527 [==============================] - 0s 90us/sample - loss: 0.0393 - accuracy: 0.9967
Epoch 10/15
1527/1527 [==============================] - 0s 93us/sample - loss: 0.0333 - accuracy: 0.9961
Epoch 11/15
1527/1527 [==============================] - 0s 97us/sample - loss: 0.0310 - accuracy: 0.9974
Epoch 12/15
1527/1527 [==============================] - 0s 95us/sample - loss: 0.0270 - accuracy: 0.9980
Epoch 13/15
1527/1527 [==============================] - 0s 93us/sample - loss: 0.0244 - accuracy: 0.9967
Epoch 14/15
1527/1527 [==============================] - 0s 95us/sample - loss: 0.0219 - accuracy: 0.9974
Epoch 15/15
1527/1527 [==============================] - 0s 91us/sample - loss: 0.0199 - accuracy: 0.9980
sample_idx = 42
plt.imshow(scaler.inverse_transform(X_test[sample_idx]).reshape(8, 8),
cmap=plt.cm.gray_r, interpolation='nearest')
plt.title("true label: %d" % y_test[sample_idx])
#获得所有测试结果的前向运算值 (概率)
probabilities = keras_model.predict_proba(X_test, verbose=0)
print("Predicted probability distribution for sample #42:")
for class_idx, prob in enumerate(probabilities[sample_idx]):
print("%d: %0.5f" % (class_idx, prob))
print()
print("Likelihood of true class for sample #42:")
p_42 = probabilities[sample_idx, y_test[sample_idx]]
print(p_42)
print()
print("Negative Log Likelihood of true class for sample #42:")
print(-np.log(p_42))
print()
print("Average negative loglikelihood of the test set:")
Y_test = to_categorical(y_test)
loglikelihoods = np.sum(np.log(probabilities) * Y_test, axis=1)
print(-np.mean(loglikelihoods))
Predicted probability distribution for sample #42:
0: 0.00001
1: 0.00258
2: 0.00007
3: 0.00000
4: 0.00043
5: 0.00001
6: 0.00004
7: 0.00000
8: 0.99674
9: 0.00011
Likelihood of true class for sample #42:
0.99674326
Negative Log Likelihood of true class for sample #42:
0.003262053
Average negative loglikelihood of the test set:
0.099366665
for sample #42:")
print(-np.log(p_42))
print()
print(“Average negative loglikelihood of the test set:”)
Y_test = to_categorical(y_test)
loglikelihoods = np.sum(np.log(probabilities) * Y_test, axis=1)
print(-np.mean(loglikelihoods))
Predicted probability distribution for sample #42:
0: 0.00001
1: 0.00258
2: 0.00007
3: 0.00000
4: 0.00043
5: 0.00001
6: 0.00004
7: 0.00000
8: 0.99674
9: 0.00011
Likelihood of true class for sample #42:
0.99674326
Negative Log Likelihood of true class for sample #42:
0.003262053
Average negative loglikelihood of the test set:
0.099366665
```python