大话数据结构学习笔记 - 图的最短路径之Floyd算法
大话数据结构学习笔记 - 图的最短路径之Floyd算法
本文是对网结构最短路径的另一求法,上一节讲的为Dijkstra算法,本节将Floyd算法, 有关于最短路径的讲解也在上一节。
Floyd算法
算法简介
弗洛伊德Floyd算法也是一种在给定的加权图中求最短路径的算法,求的所有顶点到所有顶点的时间复杂度为 O(n3) O ( n 3 ) , 是由1978年的图灵获得者、斯坦福大学计算机科学系教授罗伯特·弗洛伊德命名。
基本思想
首先定义两个二维数组D[MAXVEX][MAXVEX]和P[MAXVEX][MAXVEX],D数组代表顶点到顶点的最短路径权值和矩阵, P代表对应顶点的最小路径前驱矩阵。 初始时,将矩阵D中顶点D[v][w]设置为顶点v到顶点w的权值,若两顶点不相连,则D[v][w] = INF。接下来对矩阵D更新, 如果D[v][w] > D[v][k] + D[k][w], k表示v、w两顶点通过中转顶点,该表达式表示通过中转顶点的权值和较小时,更新v、w权值和。下面通过实例进行演示
算法图解
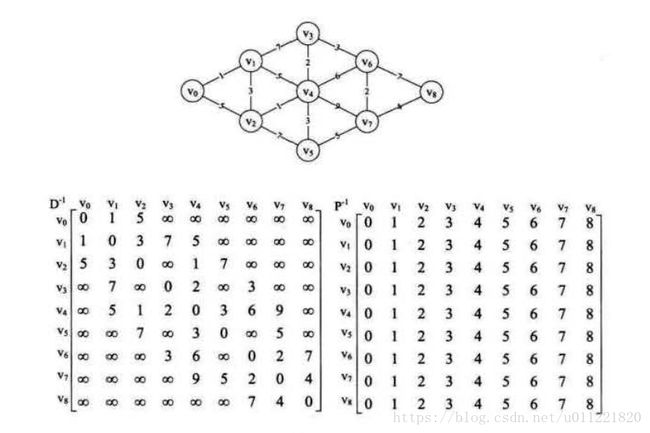
初始状态:初始化P和D矩阵, D表示顶点到顶点的权值, P表示顶点v到顶点w的最短路径。若顶点之间直接相连,则D矩阵值为权值,否则为无穷大。
第一步: 首先以第一个顶点v0为中转点, 即所有的顶点都经过v0中转,计算是否有最短路径的变化,结果没有
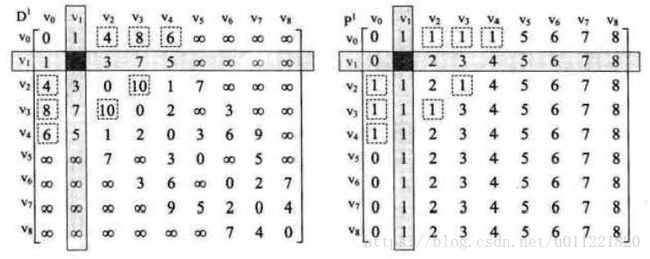
第二步: 以v1顶点为中转点,即所有顶点都经过v1中转, 可以看到,D[0][2] > D[0][1] + D[1][2], 即表示以v1为中转点,顶点v0到v2的权值和变小了,即D[0][2] = 4, 同理可得D[0][3] = 8, D[0][4] = 6, 然后更新D矩阵和P矩阵
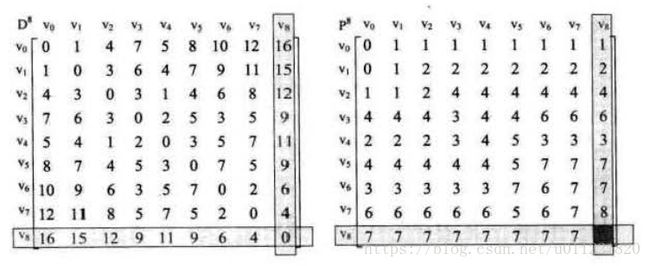
第三步: 接下来,依次以每个顶点作为中转点, 得到以每个顶点做为中转点后的权值, 得到最终的矩阵D和矩阵P
代码
无向图结构
#define MAXVEX 9
#define INF 65535
typedef int Patharc[MAXVEX][MAXVEX];
typedef int ShortPathTable[MAXVEX][MAXVEX];
typedef struct
{
int vexs[MAXVEX];
int arc[MAXVEX][MAXVEX];
int numVertexes, numEdges;
}MGraph;算法
/* Floyd 算法, 求网图 G 中各顶点 v 到其余顶点 w 的最短路径 P[v][w] 及带权长度 D[v][w] */
void ShortestPath_Floyd(MGraph G, Patharc *P, ShortPathTable *D) {
/* 初始化 D 与 P */
for (int v = 0; v < G.numVertexes; ++v) {
for (int w = 0; w < G.numVertexes; ++w) {
(*D)[v][w] = G.arc[v][w]; /* D[v][w] 值即为对应顶点间的权值 */
(*P)[v][w] = w; /* 初始化 P */
}
}
for (int k = 0; k < G.numVertexes; ++k) {
for (int v = 0; v < G.numVertexes; ++v) {
for (int w = 0; w < G.numVertexes; ++w) {
if ((*D)[v][w] > (*D)[v][k] + (*D)[k][w]) {
/* 如果经过下标为 k 的顶点路径比原两点间路径更短 */
(*D)[v][w] = (*D)[v][k] + (*D)[k][w]; /* 将当前两点间权值设为更小的一个 */
(*P)[v][w] = (*P)[v][k]; /* 路径设置为经过下标为 k 的顶点 */
}
}
}
}
}打印各顶点间的最短路径
/* 打印各顶点间的最短路径 */
void ShowShortestPath(MGraph G, Patharc *P, ShortPathTable *D)
{
for(int v = 0; v < G.numVertexes; ++v)
{
for(int w = v + 1; w < G.numVertexes; ++w)
{
printf("v%d-v%d weight: %d ",v,w,(*D)[v][w]);
int k = (*P)[v][w]; /* 获得第一个路径顶点下标 */
printf(" path: %d",v); /* 打印源点 */
while (k != w) /* 如果路径顶点下标不是终点 */
{
printf(" -> %d",k); /* 打印路径顶点 */
k = (*P)[k][w]; /* 获得下一个路径顶点下标 */
}
printf(" -> %d\n",w); /* 打印终点 */
}
printf("\n");
}
}源码
邻接矩阵最短路径之Floyd算法
结语
关于图的最短路径的两种方法都已整理,继续加油go go go