Simulink入门（二）

关注“嵌入式软件学习圈”免费获取更多学习教程

一、数值的输出格式

•（1）数值型数据

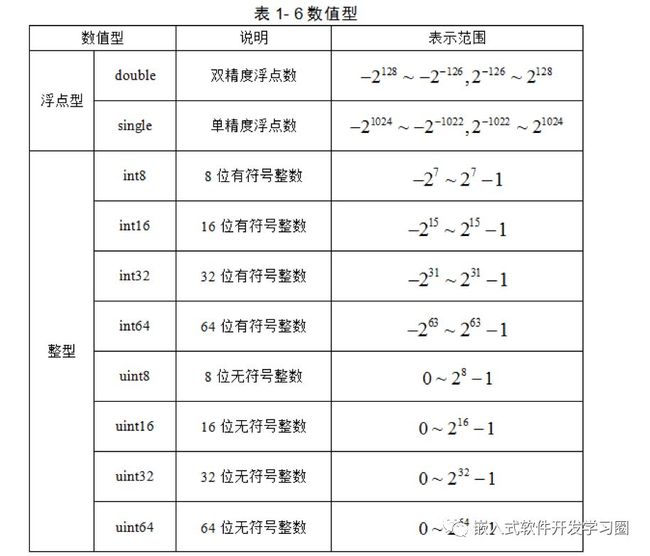
•MATLAB数值型数据包括整数（有符号和无符号）和浮点数（单精度和双精度），表1-6列出了数值型的不同格式。需要注意的是，在缺省状态下，数据类型默认为双精度的浮点数。

 

 

（2）MATLAB的数值精度

•MATLAB所能表示的最小实数称为MATLAB的数值精度，在MATLAB 7以上版本中，MATLAB的数据精度为，任何绝对值小于的实数，MATLAB都将其视为0。

•在MATLAB命令窗口输入命令如下：

•clc,clear,closeall

•format long

•x1 = 2^-3

•x2 = 2^30 

•运行程序输出结果如下：

•x1 =

•  0.125000000000000

•x2 =

•    1.073741824000000e+09

 

（3）MATLAB的显示精度

 

•MATLAB所能显示的有效位数称为MATLAB的显示精度。默认状态下，若数据为整数，则以整型显示；若为实数，则以保留小数点后4位的浮点数显示。

•MATLAB的显示格式可由format函数控制，需要注意的是，format函数并不改变原数据，只影响其在命令窗中的显示。此外还可以使用digits和vpa函数来控制显示精度

•分别使用format，short，rat，digits和vpa函数控制显示精度，在MATLAB命令窗口输入命令如下：

 

•clc,clear,closeall

•pi

•format long

•pi

•format short

•pi

•format rat

•pi

•digits(10);

•vpa(pi)

•vpa(pi,15)

 

•运行程序输出结果如下：

•

•ans=

•  3.141592653589793

•ans=

•  3.141592653589793

•ans=

•   3.1416

•ans=

•    355/113   

•ans=

•3.141592654

•ans=

•3.14159265358979

 

 

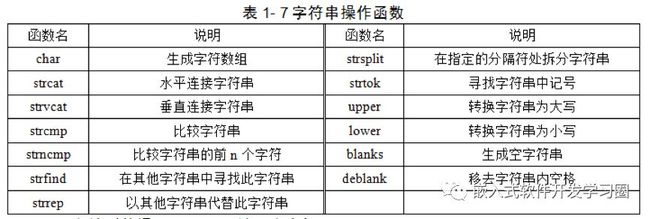
•类似于其他高级语言，MATLAB的字符和字符串运算也相当强大。在MATLAB中，字符串可以用单引号（'）进行赋值，字符串的每个字符（含空格）都是字符数组的一个元素。MATLAB还包含很多字符串相关操作函数，具体见表1-7。

 

 

 

 

•对于字符型数据，MATLAB输入命令如下：

•clc,clear,closeall

•symsa b

•y=a

•运行程序输出结果如下：

•>> y

•y =

•a

•字符串的相减运算操作如下：

•y1 = a+1

•y2 = y1-2

•运行程序输出结果如下：

•y1 =

•a + 1

•y2 =

•a – 1

•字符串的相加运算操作如下：

•y3=y+y1

•运行程序输出结果如下：

•>> y+y1

•ans=

•2*a + 1

•字符串的相乘运算操作如下：

•y4=y*y1

•运行程序输出结果如下：

•>> y4=y*y1

•y4 =

•a*(a + 1)

•字符串的相除运算操作如下：

•y5=y/y1

•运行程序输出结果如下：

•>> y5=y/y1

•y5 =

•a/(a + 1)

•

 

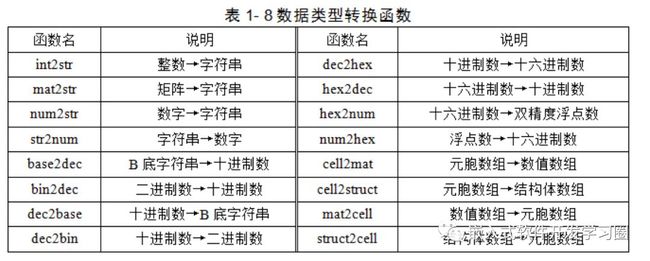
•MATLAB支持不同数据类型间的转换，这给数据处理带来极大方便，常用的数据类型转换函数如表1-8所示。

 

 

• 

•字符型变量转换，命令如下：

•clc,clear,closeall

•a = 'pi'

•b=double(a)

•b1=str2num(a)

•c=11*a

•d=11*b

•d=11*b1

•运行程序输出结果如下：

•a =

•    pi

•b =

•    112            105       

•b1 =

•    355/113   

•c =

•   1232           1155       

•d =

•   1232           1155       

•d =

•   3905/113 

 

 

•1．M文件的类型

•（1）脚本M文件

•（2）函数M文件

•2．M文件的结构

 

•1.4.2  MATLAB程序控制语句运用

 

•1．程序分支控制语句

•程序分支控制语句包括if结构和switch结构语句，if与else或elseif连用，偏向于是非选择，当某个逻辑条件满足时执行if后的语句，否则执行else语句。

•switch和case、otherwise连用，偏向于各种情况的列举，当表达式结果为某个或某些值时，执行特定case指定的语句段，否则执行otherwise语句。其中if语句在实际编程中运用较多，具体的if语句句法形式如下所示：

 

•clc,

•clear,

•close all

•a=1;

•if a==1

•   b=0

•else

•   b=1

•end

•运行程序输出结果如下：

•b =

•    0

•如果a=2，继续运行程序，

•clc,clear,closeall

•a=11;

•switch a

•   case 1

•   b=0

•   otherwise

•   b=1

•end

•运行程序输出结果如下：

•b =

•      1       

•

 

2．程序循环控制语句

 

•循环控制语句使用能够使用处理大规模的数据，能够循环进行数据处理，特别是矩阵的运算，一个矩阵包括M行N列，通常需要对M行N列均进行处理，因此循环语句显得尤为重要，MATLAB中提供了两类循环语句，分别是for循环和while循环：

•for循环指定了循环的次数， 如M行数据处理，则循环M次。

•while循环则判别等式是否成立，若成立继续在循环体中运行，若不成立则跳出循环体，如果设置参数不合理，则可能导致死循环，因此在使用while时，应该注意判别语句的使用。

•与for和while搭配的接触循环的语句有end、break、continue等等，end表示循环结束，break表示内嵌判别语句下的结束循环，continue语句使得当前次循环不向下执行，直接进入下一次循环。

3．程序终止控制语句

 

•for循环直接指定循环的次数，具体的语法格式如下：

•clc,

•clear,

•close all

•a=0

•for i=1:3

•   a=a+1

•end

•运行程序输出结果如下：

•a =

•    0

•a =

•    1

•a =

•    2

•a =

•    3

 

•1.5.1  离散数据图形绘制

•一个二元实数标量对(x0, y0)可以用平面上的点来表示，一个二元实数标量数组[(x1, y1) (x2, y2) … (xn, yn)]可以用平面上的一组点来表示，对于离散函数Y=f(X)，当X为一维标量数组X=[x1, x2, … ,xn]时，根据函数关系可以求出Y相应的为一维标量Y=[y1, y2, … ,yn]。

•当把这两个向量数组在直角坐标系中用点序列来表示时，就实现了离散函数的可视化。

•应当注意的是，MATLAB是无法实现对无限区间上的数据的可视化的。

 

 

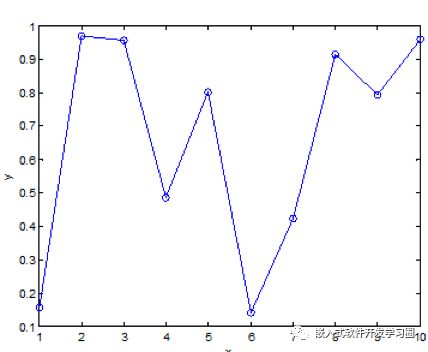
•【例3-1】离散数据的图形绘制

•clc,clear,closeall

•x=1:10;

•y=rand(10,1);

•plot(x,y,'bo-')

•xlabel('x')

•ylabel('y')

•运行该程序文件，得到图形

 

 

1.5.2  函数图形绘制

 

•在MATLAB中，是无法画出真正的连续函数的，只是将步长尽量取到最小，因此在实现连续函数的可视化时，首先也必须将连续函数用在一组离散自变量上计算函数结果，然后将自变量数组和结果数组在图形中表示出来。

•当然，这些离散的点还是不能表现函数的连续性的，为了更形象地表现函数的规律及其连续变化，通常采用以下两种方法：

•（1）对离散区间进行更细的划分，逐步趋近函数的连续变化特性，直到达到视觉上的连续效果；

•（2）把每两个离散点用直线连接，以每两个离散点之间的直线，来近似表示两点间的函数特性。

 

 

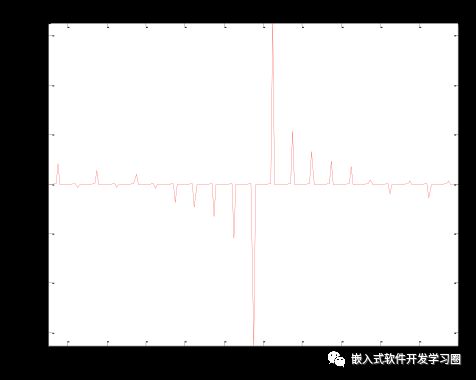
•clc,clear,closeall

•x=-11:0.1:10;

•y=tan(x*pi);

•plot(x,y,'r--')

•xlabel('x')

•ylabel('y')

•axis tight

 

 

1.5.3网格图绘制

•三维网格图和曲面图的绘制比三维曲线图的绘制稍显复杂，主要是因为：绘图数据的准备以及三维图形的色彩、明暗、光照和视角等的处理。绘制函数z=f(x,y)的三维网格图的过程如下：

•1．确定自变量x和y的取值范围和取值间隔如下：

•x=x1:dx:x2, y=y1:dy:y2

•2．构成xoy平面上的自变量采样个点矩阵

•（1）利用“格点”矩阵的原理生成矩阵

•x=x1:dx:x2; y=y1:dy:y2;

•X=ones(size(y))*x;

•Y=y*ones(size(x));

•（2）利用meshgrid指令生成“格点”矩阵

•x=x1:dx:x2; y=y1:dy:y2;

•[X,Y]=meshgrid(x,y);

•3．计算在自变量采样“格点”上的函数值：Z=f(X,Y)

•绘制网格图的基本mesh指令的句法格式如下：

•（1）mesh(X,Y,Z)

•其功能为以X为x轴自变量、Y为y轴自变量，绘制网格图；XY均为向量，若X、Y长度分别为m、n，则Z为m´n的矩阵，即[m,n]=size(Z)，则网格线的顶点为(Xj,Yi,Zij)。

•（2）mesh(Z)

•其功能为以Z矩阵列下标为x轴自变量、行下标为y轴自变量，绘制网格图；

•（3）mesh(X,Y,Z,C)

•其功能为以X为x轴自变量、Y为y轴自变量，绘制网格图；其中C用于定义颜色，如果不定义C，则成为mesh(X,Y,Z)，其绘制的网格图的颜色随着Z值（即曲面高度）成比例变化，

•（4）mesh(X,Y,Z,’PropertyName’,PropertyValue,…)

•其功能为以X为x轴自变量、Y为y轴自变量，绘制网格图；PropertyValue用来定义网格图的标记等属性。

•

•1）观察meshgrid指令的效果，编写程序如下：

•clc,clear,closeall

•a=-0.98;b=0.98;c=-1;d=1;n=10;

•x=linspace(a,b,n); y=linspace(c,d,n);

•[X,Y]=meshgrid(x,y);

•plot(X,Y,'+')

•运行程序输出图形如图1-14所示。

 

 

 

 

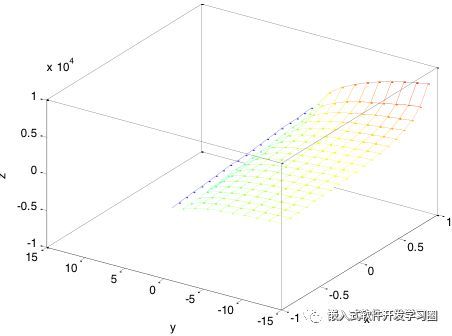
•2）做函数的定义域裁剪，观察上述三维绘图指令的效果，编程如

•下：

•clear,clf,

•a=-1;b=1;c=-15;d=15;n=20;eps1=0.01;

•x=linspace(a,b,n);y=linspace(c,d,n);

•[X,Y]=meshgrid(x,y);

•for i=1:n                             %计算函数值z ，并作定义域裁剪

•   for j=1:n

•    if (1-X(i,j))

•       z(i,j)=NaN;                   %作定义域裁剪，定义域以外的函数值为NaN

•    else

•       z(i,j)=1000*sqrt(1-X(i,j))^-1.*log(X(i,j)-Y(i,j));  

•    end

•  end

•end                  

•zz=-20*ones(1,n);plot3(x,x,zz),gridoff,holdon        %画定义域的边界线

•mesh(X,Y,z)                %绘图，读者可用meshz,  surf,  meshc在此替换之

•view([-56.5 38]);

•xlabel('x'),ylabel('y'),zlabel('z'),   box on     %把三维图形封闭在箱体里

•

•

 

 

关注微信公众号“Auto笔记”获取更多嵌入式学习资讯

如需获取其他学习资料，直接在微信公众号留言