二分搜索树的设计思路以及常见的操作实现
文章目录
- 二分查找树是个啥?
- 二分查找树的 add 操作
- 二分查找树的 contains 操作
- 二分查找树的深度遍历
- 深度优先遍历非递归实现
- 二分查找树广度优先遍历
- minimum 和 maximum
- 查询 minimum 和 maximum
- 删除 minimum 和 maximum
- 删除二叉树的任意结点
- 打印树形二分查找树
- 全部实现代码
二分查找树是个啥?
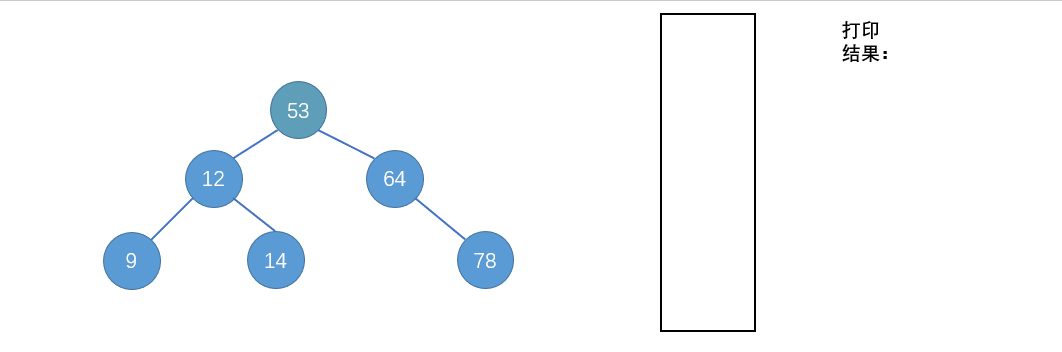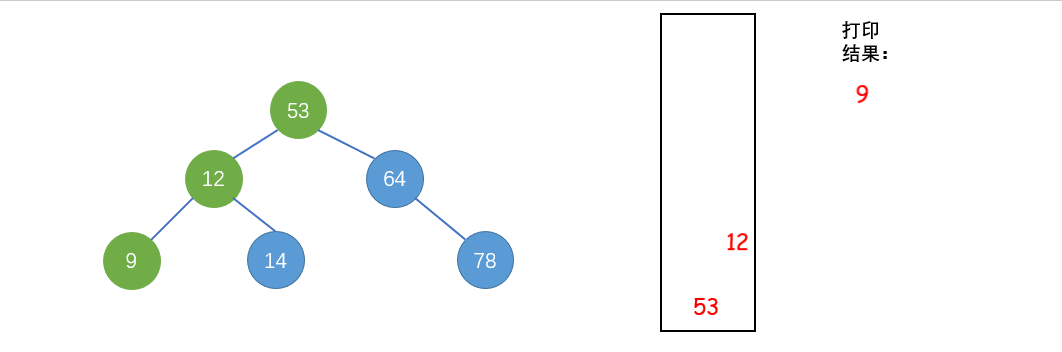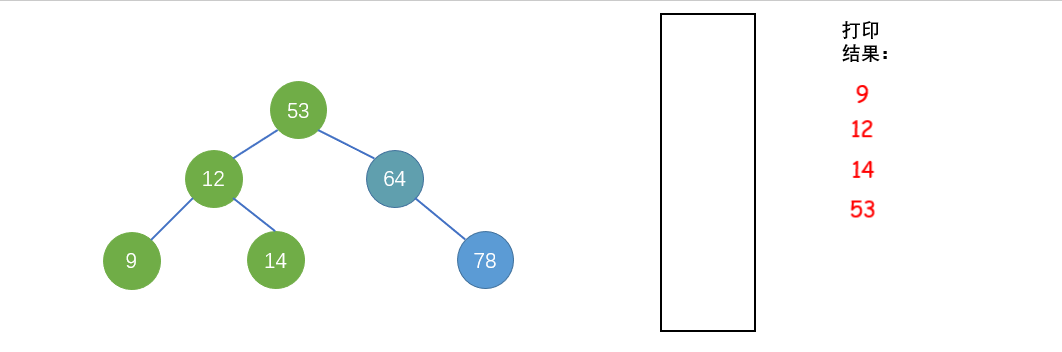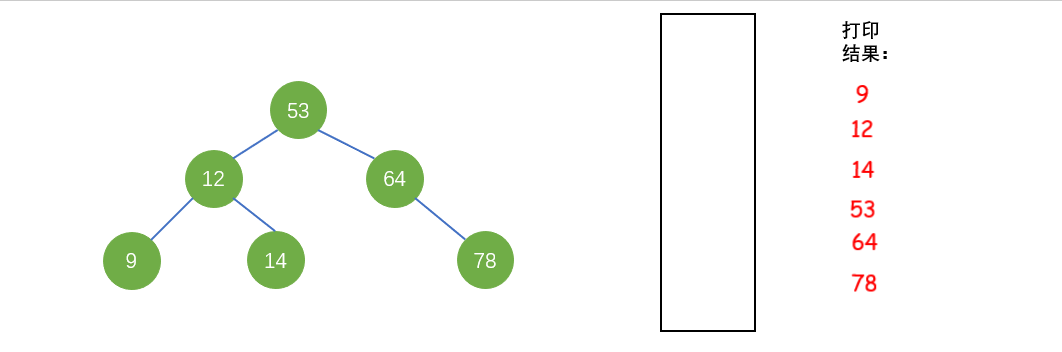
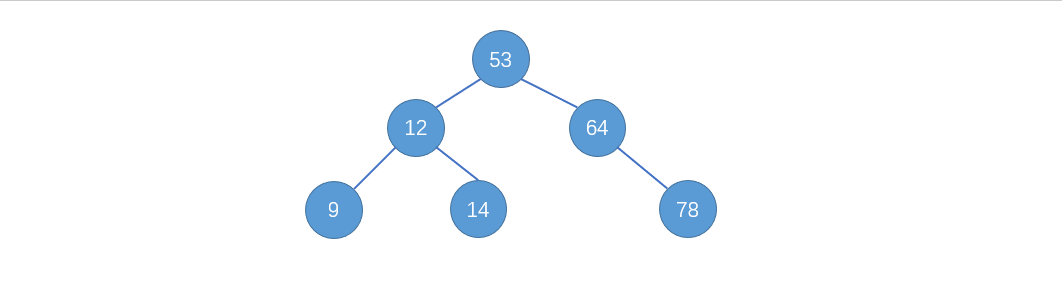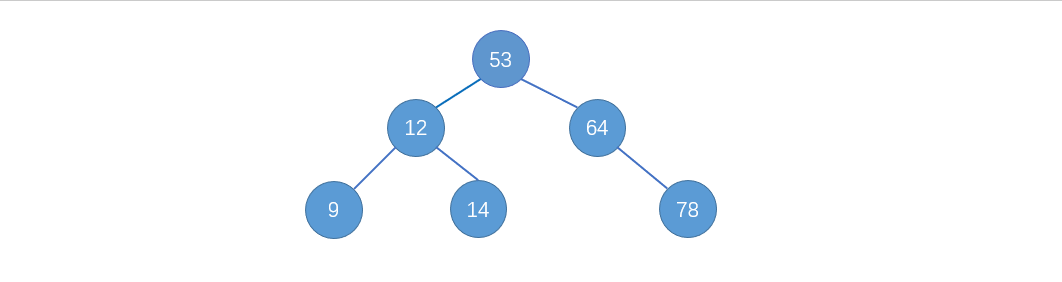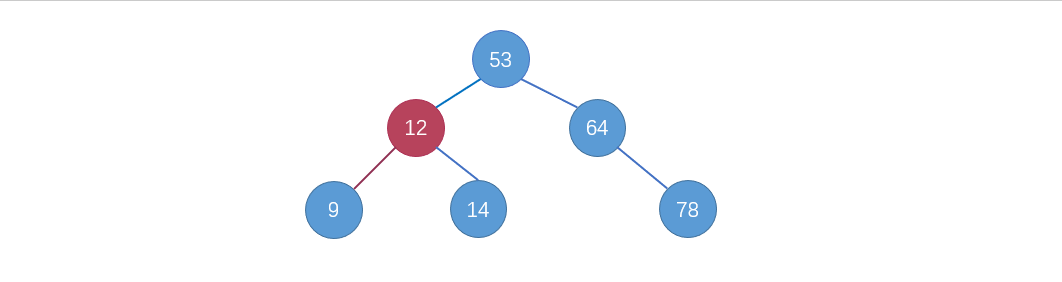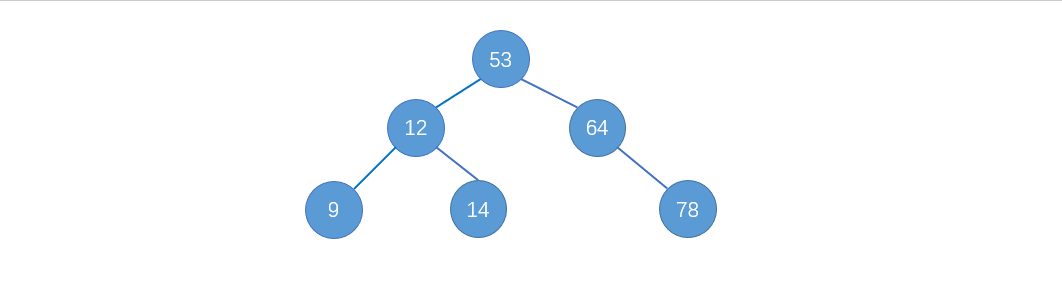
二分查找树(binary search tree),也叫二分搜索树。可以说是二叉树的一个应用,也是二叉树的一种数据结构,如图:

特点:对于每一个结点,左孩子小于该节点,有孩子大于该结点。
既然是二叉树,同样是一种动态数据结构,可以使用结点类来存放每个结点,如下:
class Node{
E e;
Node left; //左孩子
Node right; //右孩子
}
树的这种结构,非常适合递归来实现各种操作,往往也是令人迷惑的场面。如果没有养成递归思想,对树的这种递归操作往往会感到迷惑,下面将剖析各种递归操作。
二分查找树的 add 操作

递归开始于 根节点,通过 return 将 新结点 链入到二叉树中。其中的情形 ① 和 ② 是递归的基准情形,递归调用在情形 ③ 和 ④ 中进行。
private Node add(Node node, E e) {
if(node == null) {
size++;
return new Node(e);
}
if(e.compareTo(node.e) < 0) {
node.left = add(node.left, e);
}
if(e.compareTo(node.e) > 0){
node.right = add(node.right, e);
}
return node;
}
Tips: 比较结点值得大小时,我们不能使用基本的操作符(我们类型选用泛型,只能是包装类和引用类,对象大小比较不能用基本操作符);需要使用 comparable 类中得 comparaTo()
二分查找树的 contains 操作
二分查找树给二叉树了一个存储的顺序,使得我们对二叉树的操作变得更简单。
查询操作未对二叉树进行更改,所以不需要 return 结点,只需要通过返回的 布尔值 来判度查找结果。
private boolean contains(Node node, E e) {
if(node == null) {
return false;
}else if(e.compareTo(node.e) == 0) {
return true;
}else if(e.compareTo(node.e) < 0) {
return contains(node.left, e);
}else{
return contains(node.right, e);
}
}
二分查找树的深度遍历
先根遍历(DLR),又名先序遍历:先访问根结点,再遍历左子树,遍历右子树。
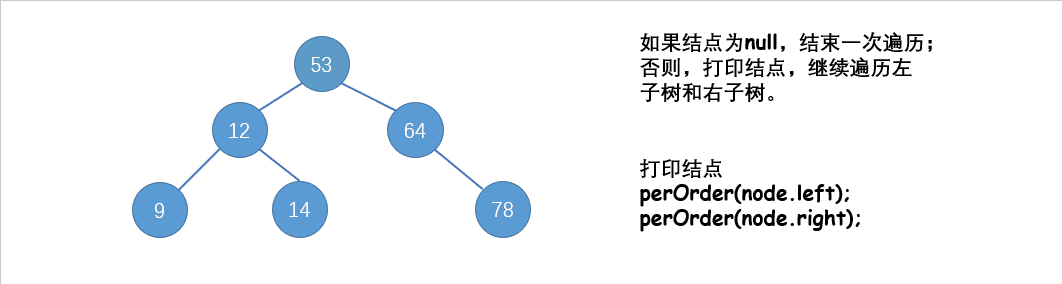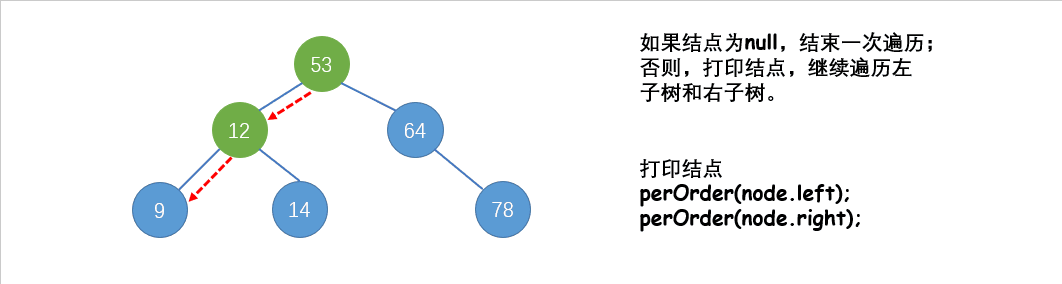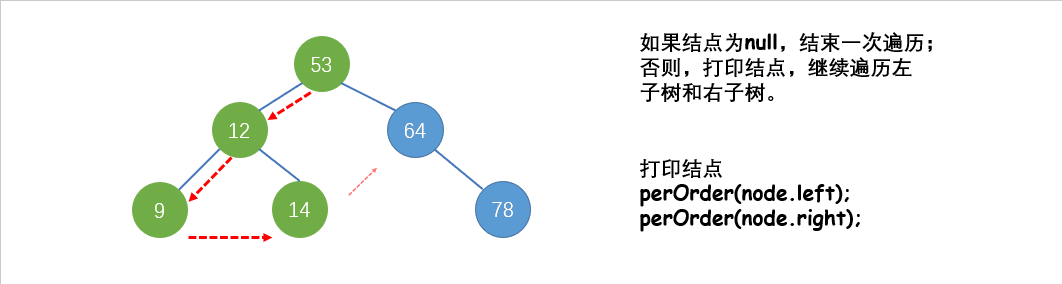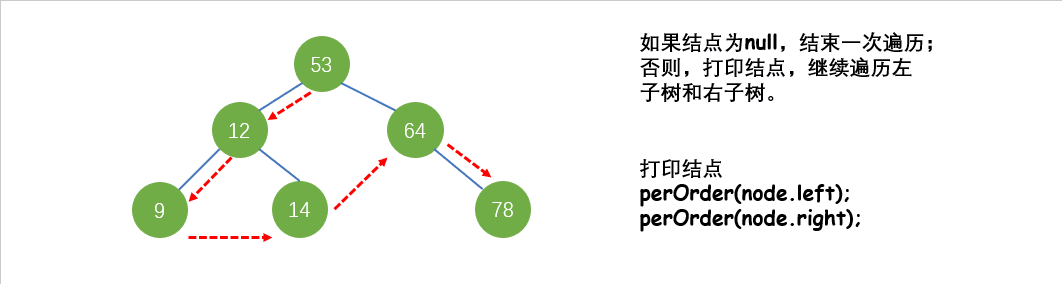
图中出现的二叉树,使用先根遍历结果为:53 12 9 14 64 78
private void perOrder(Node node) {
//DLR
if(node == null)
return;
else {
System.out.print(node.e+" ");
perOrder(node.left);
perOrder(node.right);
}
}
中序遍历(LDR),又名对称遍历:先遍历左子树,再访问根结点,遍历右子树。

图中出现的二叉树,使用中遍历结果为:9 12 14 53 64 78
private void inOrder(Node node) {
//LDR
if(node == null)
return;
else {
inOrder(node.left);
System.out.print(node.e+" ");
inOrder(node.right);
}
}
后序遍历(LRD):先遍历左子树,再遍历右子树,再访问根结点。
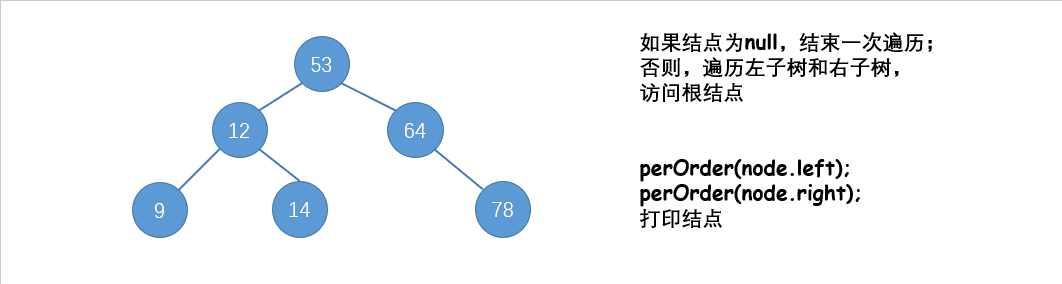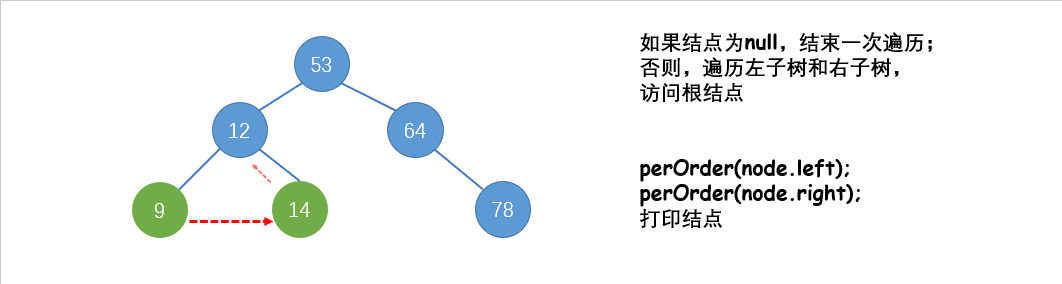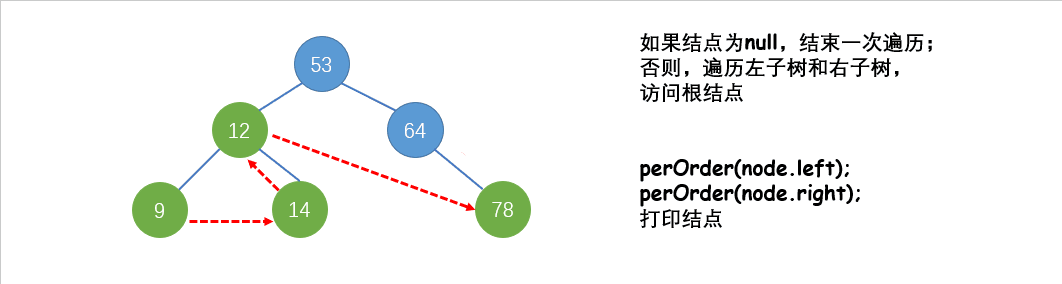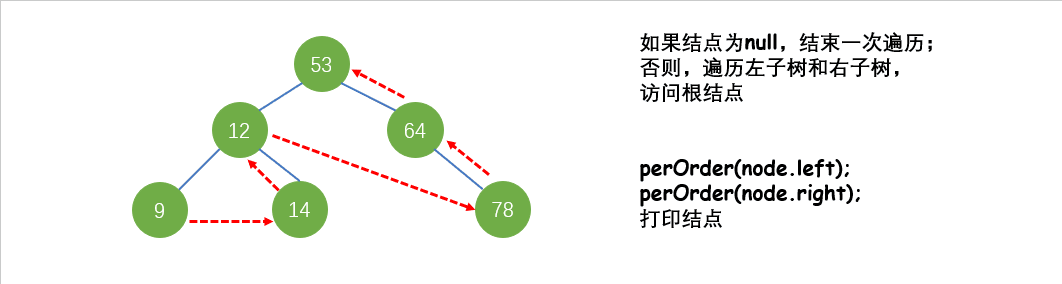
图中出现的二叉树,使用后序遍历结果为:9 14 12 78 64 53
private void postOrder(Node node) {
//LRD
if(node == null)
return;
else {
postOrder(node.left);
postOrder(node.right);
System.out.print(node.e+" ");
}
}
看了三种遍历方式,发现虽然顺序有差异,但在编程时,集中体现为打印语句的顺序不同;正是由于递归调用前后语句的执行深度和顺序不同,支持了树的深度遍历。
Tips: 深度遍历是根据递归来定义的,默认的方向是从左到右遍历,也可以从右向左遍历,称这种遍历顺序为逆序遍历。
深度优先遍历非递归实现
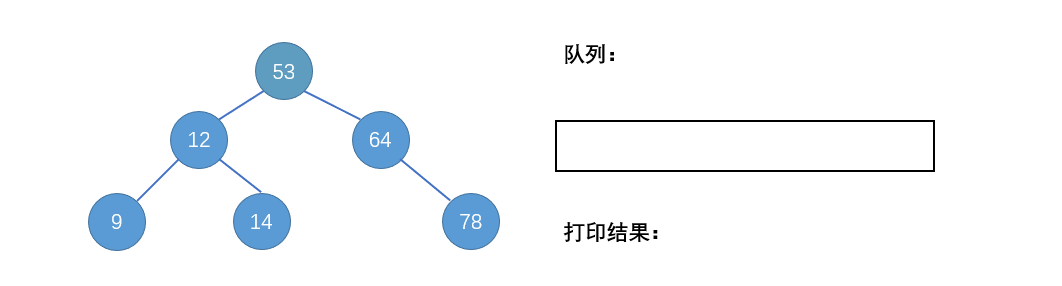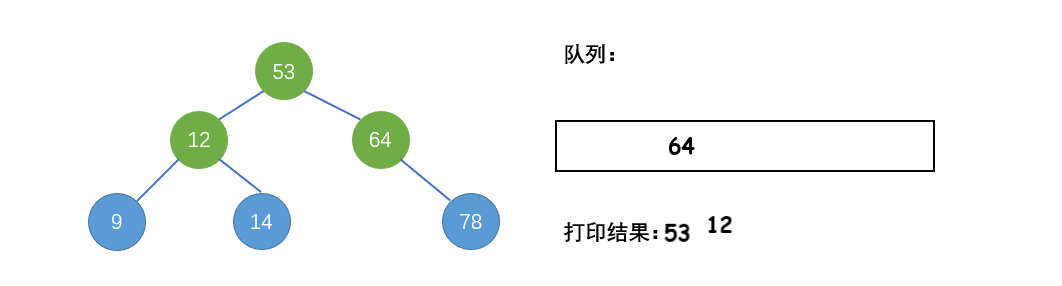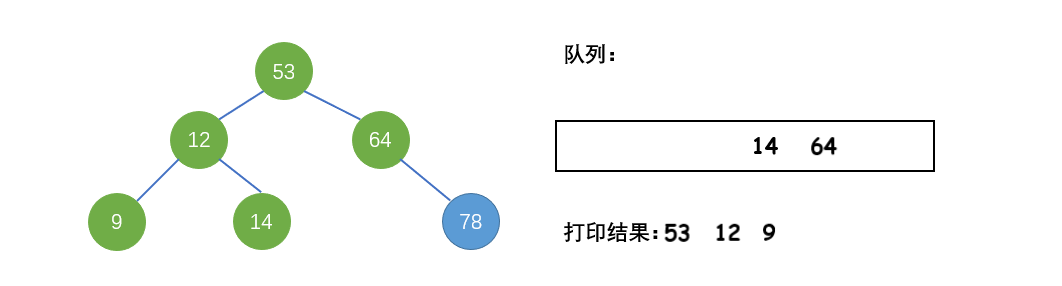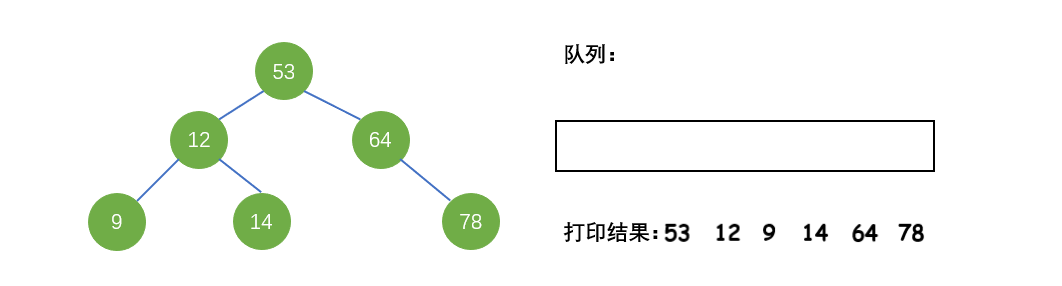
先序遍历(DLR):利用队列来辅助实现遍历
算法思路
将根结点入队,当队列不为空时,重复下面步骤:
① 出队队头结点
② 打印队头结点
③ 判断队头结点左子树是否为空。如果左子树为空,入队队头结点的右子树(若右子树不为空);否则,入队队头结点的左子树和右子树(若右子树不为空),同时,保证左子树永远在队头
public void preOrder() {
//先序遍历(前序遍历)
if(root == null)
return;
Queue<Node> que = new LinkedList<>();
que.add(root);
while(!(que.isEmpty())) {
Node node = que.remove();
if(node.left == null) {
System.out.print(node.e+" ");
if(node.right != null)
que.add(node.right);
}else {
System.out.print(node.e+" ");
int n = que.size();
que.add(node.left);
if(node.right != null)
que.add(node.right);
for(int i = 0; i < n; i++) {
que.add(que.remove());
}
}
}
}
中序遍历(LDR):利用栈来实现遍历
从根节点开始,当结点不为空或者栈不为空时,重复下面步骤:
① 当前结点不为空,入队当前结点,遍历左子树至空树
② 当前结点为空,出队栈顶结点并打印,遍历右子树
public void inOrder() {
Stack<Node> stack = new Stack<>();
Node node = root;
while(node != null || !(stack.isEmpty())) {
if(node != null) {
stack.push(node);
node = node.left;
}else {
node = stack.pop();
System.out.print(node.e+" ");
node = node.right;
}
}
}
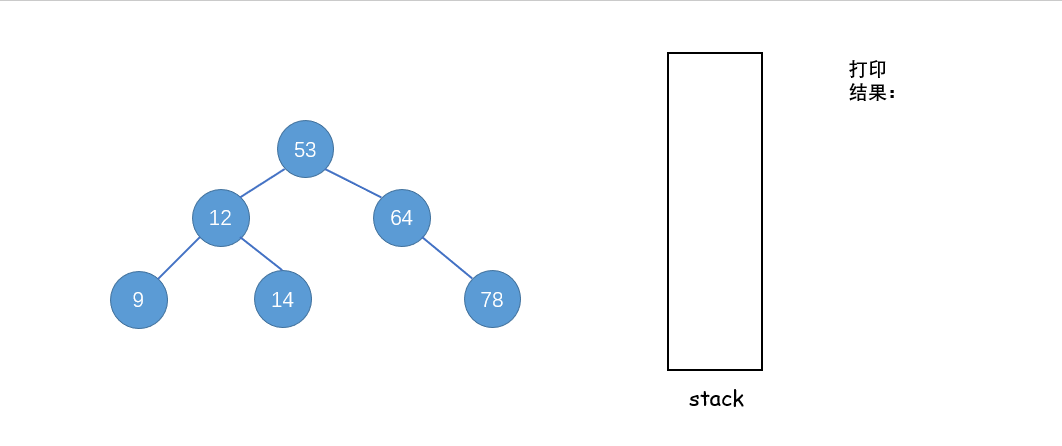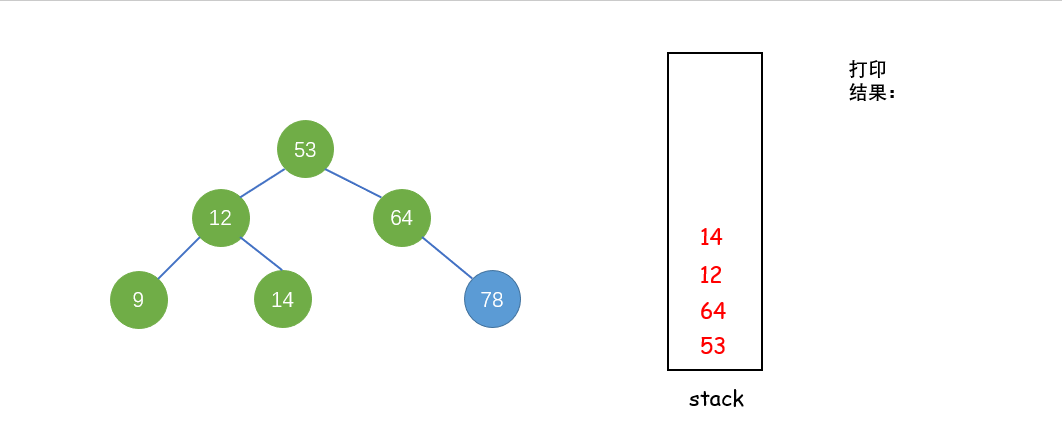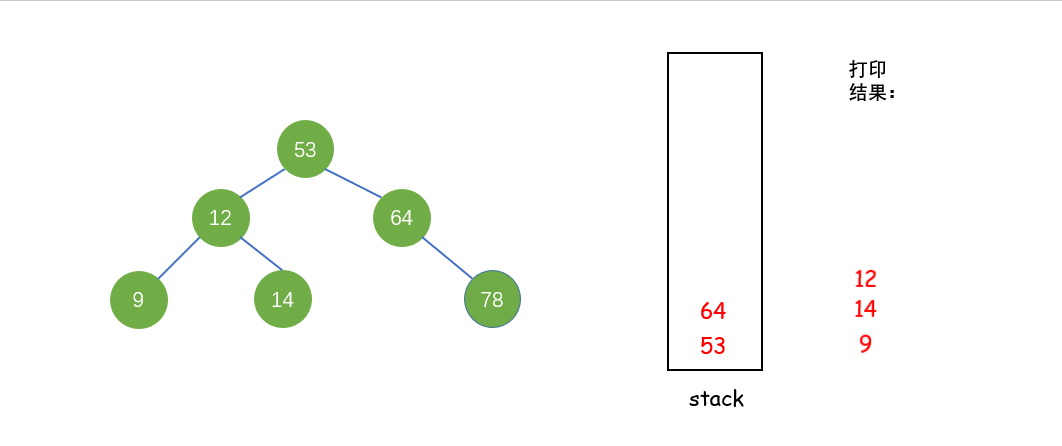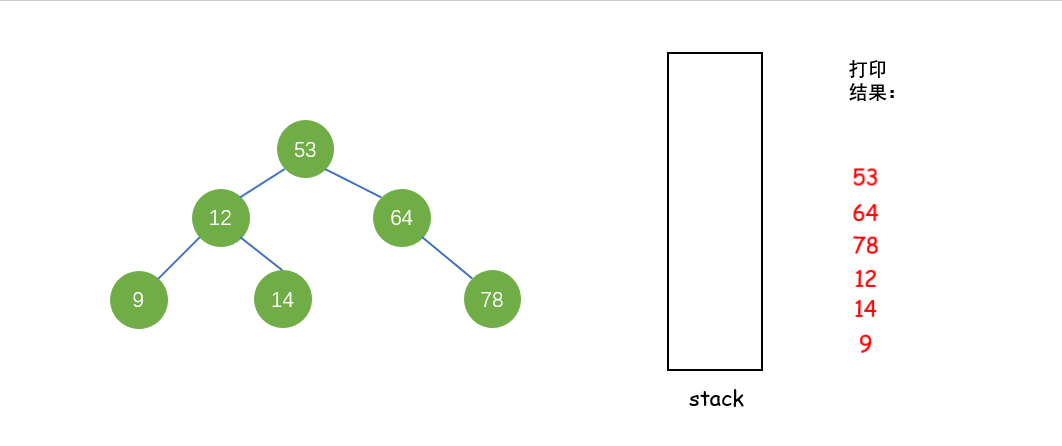
后序遍历(LRD):利用栈来实现遍历
算法思路
从根节点开始,当结点不为空或者栈不为空时,重复下面步骤:
① 当前结点不为空,入栈当前结点和有孩子(右孩子不为空),遍历右子树至空树
② 当前结点为空,栈顶元素右子树为空或者右孩子刚访问过了,出栈并打印栈顶结点,将当前结点设置为刚被访问;否则,遍历右子树
public void postOrder() {
//后序遍历(后根遍历)
Stack<Node> stack = new Stack<>();
Node node = root;
Node visited = null;
while(node!=null || !stack.isEmpty()) {
if(node != null) {
stack.push(node);
if(node.right != null)
stack.push(node.right);
node = node.left;
}else {
node = stack.pop();
if(node.right == null || node.right == visited) {
System.out.print(node.e+" ");
visited = node;
node = null;
}else {
stack.push(node);
node = node.right;
}
}
}
}
二分查找树广度优先遍历
广度优先遍历,又名层次遍历,按照每一层一次遍历所有结点,这里我们借助队列来实现。

从根结点开始,首先入队根结点,重复下面步骤:如果队头结点左右孩子不为空,出队头结点并打印,入队左右孩子结点;否则出队头结点并打印。
public void levelOrder() {
//层序遍历
Queue<Node> temporary = new LinkedList<>();
temporary.add(root);
while(!temporary.isEmpty()) {
Node node = temporary.remove();
if(node.left != null)
temporary.add(node.left);
if(node.right != null) {
temporary.add(node.right);
}
System.out.print(node.e+" ");
}
}
minimum 和 maximum
minimum 和 maximum 表示二叉查找树中的最小值和最大值,关于最大值和最小值有两种操作,查找二叉查找树中的最大值和最小值,并可以删除最大值,最小值。
查询 minimum 和 maximum
二叉查找树中的最大值和最小值,必定为深度最大的左子树和深度最大的右子树,这样直接使用递归就可以进行操作,查询并没有改变二叉树,所以无需改变根结点。
private Node minimum(Node node) {
if(node.left != null) {
return minimum(node.left);
}else {
return node;
}
}
private Node maximum(Node node) {
if(node.right != null) {
return maximum(node.right);
}else {
return node;
}
}
删除 minimum 和 maximum
删除操作会改变二叉查找树的结点,首先遍历左(右)子树,至空树(即到达二分查找树的最大和最小值结点),将最小值(最大值)接点的右子树链入到前驱结点。
private Node removeMinimum(Node node) {
if(node.left == null) {
Node rightNode = node.right;
node.right = null;
size--;
return rightNode;
}else {
node.left = removeMinimum(node.left);
return node;
}
}
private Node removeMaximum(Node node) {
if(node.right == null) {
Node leftNode = node.right;
node.left = null;
size--;
return leftNode;
}else{
node.right = removeMaximum(node.right);
return node;
}
}
Tips: 删除结点时,并不能采用循环迭代方法查找并将结点值置为 null 来完成删除;我们在所有的二叉树代码中看到的都是结点的引用,并不能删除结点,我们只能改变结点的引用,将其指向 null,并将删除结果链入二叉树中,没有引用指向的结点 ,会被垃圾回收机制回收。
删除二叉树的任意结点
首先,我们了解一下删除的规则:
① 要删除的结点没有右子树,直接将要删除结点的左子树链入到前驱结点的左子树
② 要删除的结点没有左子树,直接将要删除结点的右子树链入到前驱结点的右子树
③ 要删除的结点有右子树,找到其右子树中的最小值结点,用最小值结点替换要删除的结点,同时,将右子树中的最小值结点删除掉
在删除结点时,我们首先要定位删除结点,根据结点值来遍历左子树和右子树,来找到并删除该节点。
private Node removeNode(Node node,E e) {
if(node == null)
return null;
if(e.compareTo(node.e) > 0) {
node.right = removeNode(node.right,e);
return node;
}else if(e.compareTo(node.e) < 0) {
node.left = removeNode(node.left,e);
return node;
}else{
if(node.left == null) {
Node rightNode = node.right;
node.right = null;
size--;
return rightNode;
}
if(node.right == null) {
Node leftNode = node.left;
node.left = null;
size--;
return leftNode;
}
Node minNode = minimum(node.right);
minNode.right = removeMinimum(node.right);
minNode.left = node.left;
return minNode;
}
}
打印树形二分查找树
通过二叉树中结点的深度不同,利用逆中序遍历,可以打印逆置 90° 的二叉树:
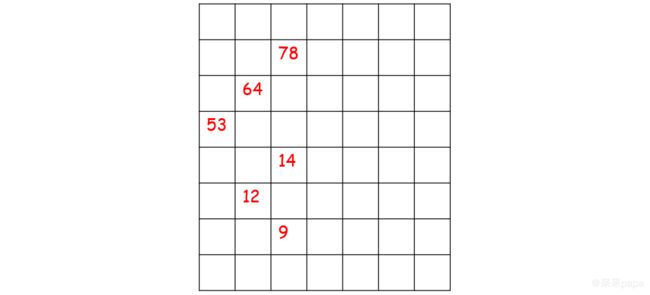
打印顺序:78 64 53 14 12 9(逆中序遍历)。每次只打印一个结点。
public void printTree() {
printTree(root, 0);
}
private void printTree(Node node, int n) {
if(node == null) {
return;
}
printTree(node.right, n+1);
for(int i = 0; i < n; i++) {
System.out.print("\t");
}
System.out.println(node.e);
printTree(node.left, n+1);
}
全部实现代码
import java.util.Queue;
import java.util.Stack;
import java.util.LinkedList;
public class BST <E extends Comparable<E>>{
private int size;
private Node root;
private class Node{
public E e;
public Node left;
public Node right;
public Node(E e) {
this.e = e;
left = null;
right = null;
}
}
public BST() {
root = null;
size = 0;
}
///获取size
public int getSize() {
return size;
}
boolean isEmpty() {
return size == 0;
}
///二分查找树添加操作
public void add(E e) {
root = add(root, e);
}
private Node add(Node node, E e) {
if(node == null) {
size++;
return new Node(e);
}
if(e.compareTo(node.e) < 0) {
node.left = add(node.left, e);
}
if(e.compareTo(node.e) > 0){
node.right = add(node.right, e);
}
return node;
}
///二分查找树查询操作
public boolean contains(E e) {
return contains(root, e);
}
private boolean contains(Node node, E e) {
if(node == null) {
return false;
}else if(e.compareTo(node.e) == 0) {
return true;
}else if(e.compareTo(node.e) < 0) {
return contains(node.left, e);
}else{
return contains(node.right, e);
}
}
///二分查找树的遍历操作
/*public void preOrder() {
//先序遍历(前序遍历)
perOrder(root);
}*/
public void preOrder() {
//先序遍历(前序遍历)
if(root == null)
return;
Queue<Node> que = new LinkedList<>();
que.add(root);
while(!(que.isEmpty())) {
Node node = que.remove();
System.out.print(node.e+" ");
if(node.left == null) {
if(node.right != null)
que.add(node.right);
}else {
int n = que.size();
que.add(node.left);
if(node.right != null)
que.add(node.right);
for(int i = 0; i < n; i++) {
que.add(que.remove());
}
}
}
}
private void perOrder(Node node) {
//DLR
if(node == null)
return;
else {
System.out.print(node.e+" ");
perOrder(node.left);
perOrder(node.right);
}
}
public void inOrder() {
//中序遍历(对称遍历)
inOrder(root);
}
/*public void inOrder() {
Stack stack = new Stack<>();
Node node = root;
while(node != null || !(stack.isEmpty())) {
if(node != null) {
stack.push(node);
node = node.left;
}else {
node = stack.pop();
System.out.print(node.e+" ");
node = node.right;
}
}
}*/
private void inOrder(Node node) {
//LDR
if(node == null)
return;
else {
inOrder(node.left);
System.out.print(node.e+" ");
inOrder(node.right);
}
}
public void postOrder() {
//后序遍历(后根遍历)
postOrder(root);
}
/*public void postOrder() {
//后序遍历(后根遍历)
Stack stack = new Stack<>();
Node node = root;
Node visited = null;
while(node!=null || !stack.isEmpty()) {
if(node != null) {
stack.push(node);
if(node.right != null)
stack.push(node.right);
node = node.left;
}else {
node = stack.pop();
if(node.right == null || node.right == visited) {
System.out.print(node.e+" ");
visited = node;
node = null;
}else {
stack.push(node);
node = node.right;
}
}
}
}*/
private void postOrder(Node node) {
//LRD
if(node == null)
return;
else {
postOrder(node.left);
postOrder(node.right);
System.out.print(node.e+" ");
}
}
public void levelOrder() {
//层序遍历
Queue<Node> temporary = new LinkedList<>();
temporary.add(root);
while(!temporary.isEmpty()) {
Node node = temporary.remove();
if(node.left != null)
temporary.add(node.left);
if(node.right != null) {
temporary.add(node.right);
}
System.out.print(node.e+" ");
}
}
///获得最小值
public E minimum() {
if(size == 0)
throw new IllegalArgumentException("Error:size为零");
return minimum(root).e;
}
private Node minimum(Node node) {
if(node.left != null) {
return minimum(node.left);
}else {
return node;
}
}
///获得最大值
public E maximum() {
if(size == 0)
throw new IllegalArgumentException("Error:size为零");
return maximum(root).e;
}
private Node maximum(Node node) {
if(node.right != null) {
return maximum(node.right);
}else {
return node;
}
}
///删除最小值
public void removeMinimum() {
if(size == 0)
throw new IllegalArgumentException("Error:size为零");
root = removeMinimum(root);
}
private Node removeMinimum(Node node) {
if(node.left == null) {
Node rightNode = node.right;
node.right = null;
size--;
return rightNode;
}else {
node.left = removeMinimum(node.left);
return node;
}
}
///删除最大值
public void removeMaximum() {
if(size == 0)
throw new IllegalArgumentException("Error:size为零");
root = removeMaximum(root);
}
private Node removeMaximum(Node node) {
if(node.right == null) {
Node leftNode = node.right;
node.left = null;
size--;
return leftNode;
}else{
node.right = removeMaximum(node.right);
return node;
}
}
public boolean removeNode(E e) {
if(contains(e)) {
root = removeNode(root, e);
return true;
}else
return false;
}
private Node removeNode(Node node,E e) {
if(node == null)
return null;
if(e.compareTo(node.e) > 0) {
node.right = removeNode(node.right,e);
return node;
}else if(e.compareTo(node.e) < 0) {
node.left = removeNode(node.left,e);
return node;
}else{
if(node.left == null) {
Node rightNode = node.right;
node.right = null;
size--;
return rightNode;
}
if(node.right == null) {
Node leftNode = node.left;
node.left = null;
size--;
return leftNode;
}
Node minNode = minimum(node.right);
minNode.right = removeMinimum(node.right);
minNode.left = node.left;
return minNode;
}
}
///打印树形二叉树
public void printTree() {
printTree(root, 0);
}
private void printTree(Node node, int n) {
if(node == null) {
return;
}
printTree(node.right, n+1);
for(int i = 0; i < n; i++) {
System.out.print("\t");
}
System.out.println(node.e);
printTree(node.left, n+1);
}
}