【专升本计算机基础】信息表示与编码(二)
文章目录
- 一、数值及其转换
- 1. 计算机内数据的处理形式
- 2. 计算机内部采用二进制的原因
- 3. 基数与数码
- 4. 常用进制标识符
- 5. 二进制逻辑运算规则
- 6. 我的错题
- 二、计算机中数值的表示
- 1. 有符号数
- 2. 浮点数:
- 三、计算机中字符的表示与编码
- 1. 基本知识
- 2. 汉字编码:
- 3. 汉字编码的实现:
- 4. 汉字编码的实现是通过区位码、国标码、机内码这三步实现的。步骤如下:
- 四、信息存储单位
- 1. 基础知识
一、数值及其转换
1. 计算机内数据的处理形式
(1)在计算机内,不管你是怎样的数据,都采用二进制编码形式表示和处理。
2. 计算机内部采用二进制的原因
(1)易于表示,技术实现简单;
(2)运算简单;
(3)适于逻辑运算;
(4) 可靠性高。
3. 基数与数码
(1)二进制的数码是0、1。基数(基)为2。
4. 常用进制标识符
(1)十进制(D)、二进制(B)、八进制(O)、十六进制(H)。
5. 二进制逻辑运算规则
(1) 逻辑与运算(AND):00=0;01=0;10=0;11=1;(全1,则为1,有0则为0);
(2) 逻辑或运算(OR):0V0=0;0V1=1;1V0=1;1V1=1;(有一则为1,全0则为0);
(3) 逻辑非运算(NOT):1=0;0=1;(全部取反)
(4) 逻辑异或运算(XOR):0⊕0=0;0⊕1=1;1⊕0=1;1⊕1=0;(相同为0,相异为1);
(5) 逻辑同或运算:0⊙0=1;0⊙1=0;1⊙0=0;1⊙1;(相同为1,相异为0);
6. 我的错题
(1)有小数的进制转换:八进制转十进制:543.21O =5 * 82+4 * 81+3 * 80+2*8(-1)+ 1 * 8(-2)
(2)可能不能完成精确转换的是二进制小数和十进制的转换。
(3)在进制计数中,数码是指一组用来表示某种数制的符号。
二、计算机中数值的表示
1. 有符号数
(1) 计算机中,因为只有0和1,为了表示有符号数,所以通常把一个数的最高位定义为符号位,0表示正,1表示负。
(2) 原码、反码和补码的计算:
① 原码是数值前直接加以符号位的表示法,对于8位二进制来说,第一位为符号位,0为正,1为负。[+7]原码= 0 0000111 ,[-7]原码= 1 0000111。
② 反码:整数的反码与原码相同,负数的反码,符号位为“1”,数值部分按位取反。[+7]反= 0 0000111 ,[-7]反= 1 1111000。
③ 补码:整数的补码和原码相同,负数的补码则是符号位为“1”,数值部分按位取反后再在末位(最低位)加一,也就是“反码+1”。 [+7]补= 0 0000111 [-7]补= 1 1111001。
(3) 数值用原码表示后,加法和减法运算可以统一使用加法器完成。
(4) 0在原码和反码中有两种表示,在补码中只有一种表示方式(补码的正0和负0表示方法相同,(忽略溢出,溢出的值会被丢掉))。正数的原、反、补码都相同。
(5) 补码的思想是为了保证正数加负数的结果正确。
① 把负数表示成加补码等于0的形式。补码就是原码补上多少就变为0 的意思。
② 负数在计算机中都是以补码形式存在的。如果要知道这个负数表示什么,需要把它转为补码形式。(一个数在计算机中存在肯定是用于计算的,而负数只有补码形式才能够正确计算,所以负数在计算机中都是以补码形式存在。)
(6)正数范围:0127;负数范围:-128-1;有符号整数的范围为:-128~127。(10000000,其加上128:10000000等于0(第九位溢出丢掉,就等于0)所以10000000表示-128)正好是2^8,256个值
2. 浮点数:
(1) 名词:-1100.11 = -1.10011*2^3
① 阶符:0(2的幂为3,3的符号,为正,正数为0)
② 阶码:3(2的幂为3)
③ 数符:1(整体的符号,为负数,1)
④ 尾数:10011(小数点后的部分,10011)
(2)定点数
① 定点整数(纯整数)。定点整数指小数点隐含在机器的最右边。定点整数为纯整数。
② 定点小数(纯小数)。定点小数约定小数点位置在符号位、有效数值部分之间。定点小数是存小数,其绝对值小于1。
(3)二进制的科学计数法
① +10.101 = +1.0101*2+1
② -0.00011 = -1.1*2-4
(4)浮点数(定点整数+定点小数)。
(5)浮点表示法包括阶码和尾数两个部分。
① 尾数用定点小数表示,尾数所占的位数确定了数的精度。尾数长,数的精确度高;
② 阶码用定点整数表示,阶码所占的位数确定了数的范围。阶码长,数的取值范围越大。
a、阶符为正时,阶码越大,数绝对值越大。
b、阶符为负时,阶码越大,数绝对值越小。(负数是以补码方式存在的。)
③ 对于不同的机器,阶码和尾数各占多少位,分别用什么码制进行表示都有具体规定。在实际应用中,浮点数的表示首先要进行规格化,即转换成一个纯小数与2^E之积,并且小数点后的第一位是1,这样的浮点数称为规格化。
(6) 单精度浮点数、双精度浮点数
① 单精度浮点数:单精度浮点数长度四个字节。
② 双精度浮点数,双精度浮点数长度八个字节,精确度更高,取值范围更广。
(3)在浮点数表示和运算中,当一个数的阶码大于机器所能表示的最大码时,产生“上溢”。上溢时机器一般不再继续运算而转入“溢出”处理。当一个数的阶码小于机器所能代表的最小阶码时产生“下溢”,下溢时一般当作“机器零”来处理。
(4)数轴上任意区间内:实数是无限个,浮点数是有限个。
① 例如四个字节表示浮点数有2^32个约40亿个。为了实现有限个数表示无限的值,所以浮点数表示数据时常采用近似值。
② 浮点数在数轴上的分布是不均匀的。

a、当阶符为负时,浮点数的绝对值小于1.
b、当阶符为正时,浮点数的绝对值大于1.
③ 数据在-1到+1的去间内,数据比较精确。越向数轴的两端延伸,数据的密度就越稀疏,不精确。
三、计算机中字符的表示与编码
1. 基本知识
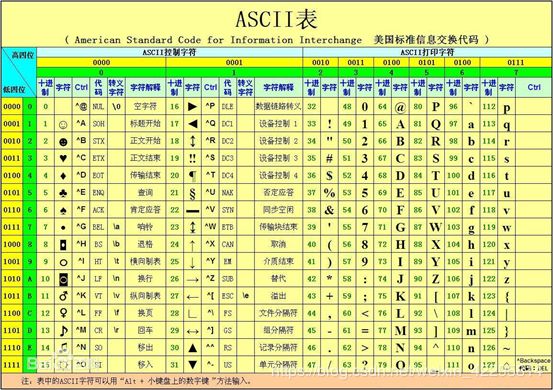
(1) 标准的ASCII码采用7位二进制编码,它可以表示2^7即128个字符,可以扩充到8位。
(2)一个字符在计算机内实际是用一个字节,8位二进制表示。
(3)字符的ascll<数字的ascll<大写字母的ascll<小写字母的ascll。
2. 汉字编码:
(1) 汉字输入码
① 音码(微软拼音、智能ABC、全拼、双拼、简拼)
② 形码(五笔字型、郑码输入法)
(2) 区位码(国际汉字库)
① 区位码的行列均有1~94(十进制)
② 每一个中文输入之后就会去汉字库中找,找到之后就转为国标码(行列各加32),再转为机内码(国标码转为16进制后行列各加80H)。
(3) 汉字国际码(交换码(国标码))
① 国标码是我国1980年发布的《信息交换用汉字编码字符集——基本集》(代号位GB 2312-80),是中文信息处理的国家标准,简称GB码。根据统计,把最常用的6763个汉字分成两级:一级汉字有3755个,按汉语拼音排列;二级汉字有3008个,按偏旁部首排列。
② 国标码可以用二进制表示。
(4) 汉字机内码(内码)
① 汉字机内码是指汉字被计算机系统内部处理和存储而使用的编码。一个国标码占两个字节。汉字机内码在国标码的基础上每个字节的最高位由0变为1,即国标码+80 80H=机内码。例如“中”的国标码位56 50H,则“中”的机内码为D6 D0H。
② 汉字内码=汉字国标码 + 8080H = 区位码+A0A0H。
③ 机内码用十六进制表示。
(4) 汉字字形码
① 用于汉字在显示屏显示或打印输出。
② 不同字体的字形描述信息存放在不同字库中(宋体、黑体等)。
3. 汉字编码的实现:
(1) 区位码的行列:1 ~ 94(十进制),国标码的行列:33 ~ 96(十进制)
(2) 国标码等于区位码的行列各+32(20H)并转为16进制。机内码为国标码的行列都加80H。计算机中真实表示汉字的就是机内码。机内码是汉字在计算机中真正的存在形式。
4. 汉字编码的实现是通过区位码、国标码、机内码这三步实现的。步骤如下:
(1) “中”:区位码:5448。
(2) 国标码的行号:54+32=86(十进制)=> 56H(十六进制);国标码的列号:48+32=80(十进制)=> 50H。国标码为5650H
(3) 机内码为国标码的行列各加80H。机内码为D6D0H。
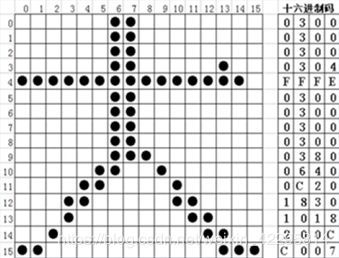
(4) 得到机内码之后要输出汉字,则需要通过字库查找汉字的字形码(16*16的方阵)。
(5) 对图形进行编码的方式称为位图,位图的基本思路是通过逐一描述图形中每一点的颜色来描述出整个图形。字形码是一个黑白图形。每一个位置只需要一位二进制数。如果一个位图采用的是256色,对颜色编码则每一个位置都需要1个字节的大小。分辨率是格子位置的个数。
四、信息存储单位
1. 基础知识
(1)位是计算机存储信息的最小单位bit。
(2)字节是计算机中用来表示存储空间大小的最基本单位Byte。
(3)存储容量=末位地址-起始位地址+1(位运算后,把单位换为B/KB/MB/GB)(最基本单位为B)。
(4)字长是指计算机同时处理信息的二进制的位数。
(5)具有字长的长度的二进制数为一个字。例如在64位机中,一个字则含有64个二进制位。
(6)一个字长为8位的存储单元可以存放0至255之间的任意一个无符号整数。
(7)一个字由若干个字节组成。
(8)信息的符号化就是数据,所以数据是信息的具体表现形式(载体)
(9)一位点阵是一个bit,所以1000个32*32点阵是125KB