临近取样算法(KNN)笔记
综述
- Cover和Hart在1968年提出了最初的临近算法
- 输入基于实例的学习(instance-based learning)
- 懒惰学习(lazy learning)
算法步骤
- 为了判断未知类别实例的类别,以所有已知类别的实例作为参照
- 选择参数K
- 计算未知实例与所有已知实例的距离
- 根据少数服从多数的投票法则(majority-voting)
- 让未知实例归类为k个最邻近样本中最多数的类别
细节(关于K)
关于距离的衡量方法:
1.Euclidean Distance定义:
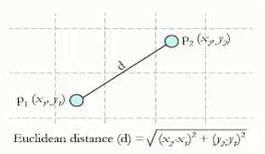
E ( x , y ) = ∑ i = 0 n ( x i − y i ) 2 E(x,y)=\sqrt{\sum\limits_{i=0}^n(x_i-y_i)^2} E(x,y)=i=0∑n(xi−yi)2
其他距离衡量:余弦值(cos),相关度(correlation),曼哈顿距离(Manhattan distance)
例子1
import math
def ComputeEuclideanDistance(x1, y1, x2, y2):
d = math.sqrt(math.pow((x1 - x2), 2) + math.pow((y1 - y2), 2))
return d
if __name__ == '__main__':
d_ag = ComputeEuclideanDistance(3, 104, 18, 90)
d_bg = ComputeEuclideanDistance(2, 100, 18, 90)
d_cg = ComputeEuclideanDistance(1, 81, 18, 90)
d_dg = ComputeEuclideanDistance(101, 10, 18, 90)
d_eg = ComputeEuclideanDistance(99, 5, 18, 90)
d_fg = ComputeEuclideanDistance(98, 2, 18, 90)
print("d_ag:",d_ag)
print("d_bg:",d_bg)
print("d_cg:",d_cg)
print("d_dg:",d_dg)
print("d_eg:",d_eg)
print("d_fg:",d_fg)
输出
d_ag: 20.518284528683193
d_bg: 18.867962264113206
d_cg: 19.235384061671343
d_dg: 115.27792503337315
d_eg: 117.41379816699569
d_fg: 118.92854997854805
由此看到最近的距离是a、b、c三个点,所以G点归类为romance
算法优缺点:
优点:
1. 简单
2. 易于理解
3. 容易实现
4. 通过对K的选择可具备丢噪音数据的键壮性
缺点:

- 需要大量空间存储所有已知实例
- 算法复杂度高(需要比较所有已知实例与要分类的实例)
- 当其样本分布不平衡时,比如其中一类样本过大(实例数量过多)占主导的时候,新的未知实例容易被归类为这个主导样本,因为这类样本实例的数量过大,但这个新的未知实例实际并没接近目标样本
改进版本
考虑距离,根据距离加上权重
比如:1/d (d:距离)
实例2
根据150个实例,实例包含萼片长度(sepal length),萼片宽度(sepal width),花瓣长度(petal length),花瓣宽度(petal width)
类别:
iris setosa, iris versicolor, iris virginica
1.利用python的机器学习库sklearn: SKLearnExample.py实现
from sklearn import neighbors
from sklearn import datasets
knn = neighbors.KNeighborsClassifier() # 调用分类器
iris = datasets.load_iris() # 返回iris数据库
# print(iris)
# iris.data为4*150矩阵的特征值,iris.target为矩阵对应的一维的对象
knn.fit(iris.data, iris.target) # 建立模型对象,同时传入数据参数
predictedLabel = knn.predict([[0.1, 0.8, 0.3, 0.9]]) # 预测
print(predictedLabel)
2.完全手写算法
import csv
import random
import math
import operator
def loadDataset(filename, split, trainingSet=[], testSet=[]):
"""
对数据进行整理
:filename: 导入数据集文件名称
:split: 区分训练集与测试集指标
:trainingSet: 训练集
:testSet: 测试集
"""
with open(filename, 'r') as csvfile:
lines = csv.reader(csvfile)
dataset = list(lines)
for x in range(len(dataset)-1):
for y in range(4):
dataset[x][y] = float(dataset[x][y])
if random.random() < split:
trainingSet.append(dataset[x])
else:
testSet.append(dataset[x])
def euclideanDistance(instance1, instance2, length):
"""
算出其k
:instance1: 表示训练集的点
:instance2: 表示预测集的点
:length: 表示维度
"""
distance = 0
for x in range(length):
distance += pow((instance1[x] - instance2[x]), 2)
return math.sqrt(distance)
def getNeighbors(trainingSet, testInstance, k):
"""
返回距离测试实例的最近的邻居
:trainingSet: 数据项
:testInstance: 一个测试实例
:k: k个数量训练集距离testInstance的label
"""
distances = []
length = len(testInstance) - 1
for x in range(len(trainingSet)):
dist = euclideanDistance(testInstance, trainingSet[x], length)
distances.append((trainingSet[x], dist))
distances.sort(key=operator.itemgetter(1)) # 获取对象第一个域里的值
print(distances)
neighbors = []
for x in range(k):
neighbors.append(distances[x][0])
return neighbors
def getResponse(neighbors):
"""
统计邻居分类的多少
:neighbors: 邻居数据
:return: 邻居分类最多的
"""
classVotes = {}
for x in range(len(neighbors)):
response = neighbors[x][-1]
if response in classVotes:
classVotes[response] += 1
else:
classVotes[response] = 1
sortedVotes = sorted(classVotes.items(), key=operator.itemgetter(1), reverse=True) # reverse按降序排列
return sortedVotes[0][0]
def getAccuracy(testSet, predictions):
"""
预测算法的精确度
:testSet: 测试集
:predictions: 算法算出的结果
"""
correct = 0
for x in range(len(testSet)):
if testSet[x][-1] == predictions[x]:
correct += 1
return (correct/float(len(testSet))) * 100.0
def main():
tariningSet = []
testSet = []
split = 0.67
print(split)
loadDataset(r'irisdata.txt', split, tariningSet, testSet)
print('Train set:' + repr(len(tariningSet)))
print('Train set:' + repr(len(testSet)))
predictions = []
k = 3
for x in range(len(testSet)):
neighbors = getNeighbors(tariningSet, testSet[x], k)
result = getResponse(neighbors)
predictions.append(result)
# print('> predicted=' + repr(result) + ', actual=')
accuracy = getAccuracy(testSet, predictions)
print('Accuracy: ' + repr(accuracy) + '%')
if __name__ == '__main__':
main()
代码以及所有用到的材料请到码云上下载:
https://gitee.com/wolf_hui/MachineLearning
