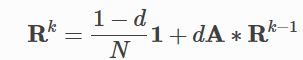DGL官方学习教程一 ——基础操作&消息传递

1.DGL Basics

图神经网络库DGL的基础操作：https://blog.csdn.net/u014281392/article/details/89436033

DGL 作者答疑！关于 DGL 你想知道的都在这里：https://mp.weixin.qq.com/s?__biz=MzI2MDE5MTQxNg==&mid=2649695390&idx=1&sn=ad628f54c97968d6fff55907c47cb77e&chksm=f276e149c501685fe8c328851132248bc3f44b994de285d073db32305b0a14cd7373f5a4780d&mpshare=1&scene=1&srcid=#rd

疑问：1.只能手动创建图?
           2.如何根据加权图权重矩阵生成图？

           3.加权图需要初始化节点特征吗？权值在API中如何传递？

2.PageRank with DGL Message Passing 

在本节中，我们将在小图上说明使用PageRank的不同级别的消息传递API的用法。在DGL中，消息传递和特征转换都是用户定义函数（UDF）。

本节目标：使用DGL消息传递接口实现PageRank。

  2.1 The PageRank Algorithm

   在PageRank的每次迭代中，每个节点（网页）首先将其PageRank值均匀地分散到其下游节点。通过聚合从其邻居接收的PageRank值来计算每个节点的新PageRank值，然后通过阻尼因子进行调整：

    PV(v) 网页v对应的PageRank值    

    N 是图中节点的数量;

    D（v）是节点v 的出度;

    N（u）是u的所有邻居节点。   

    d  阻尼因子

 

 2.2 A naive implementation   

import networkx as nx
import matplotlib.pyplot as plt
import torch
import dgl

N = 100  # number of nodes
DAMP = 0.85  # damping factor阻尼因子
K = 10  # number of iterations
g = nx.nx.erdos_renyi_graph(N, 0.1) #图随机生成器，生成nx图
g = dgl.DGLGraph(g)                 #转换成DGL图
nx.draw(g.to_networkx(), node_size=50, node_color=[[.5, .5, .5,]])  #使用nx绘制，设置节点大小及灰度值
plt.show()

根据该算法，PageRank由典型的分散 - 聚集模式中的两个阶段组成。我们首先将每个节点的PageRank值初始化为1/N，并将每个节点的out-degree存储为节点特征：

g.ndata['pv'] = torch.ones(N) / N  #初始化PageRank值
g.ndata['deg'] = g.out_degrees(g.nodes()).float()  #初始化节点特征

然后我们定义message函数，它将每个节点的PageRank值除以其out-degree，并将结果作为消息传递给它的邻居：

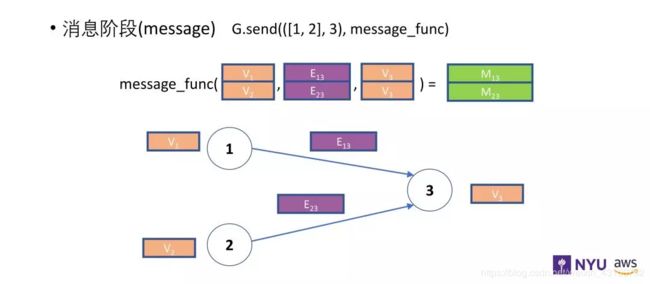
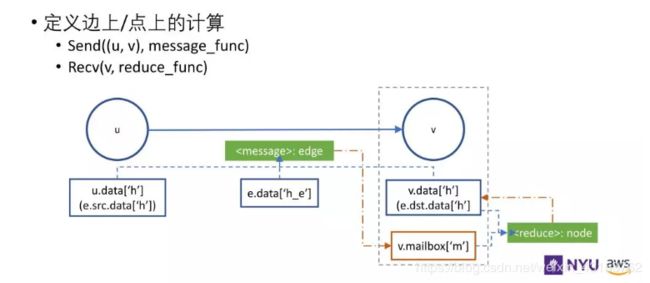
消息函数通过边获得变量，用 e.src.data 获得这条边出发节点的特征信息，通过 e.dst.data 获得目标节点的特征信息。边也拥有自己的特征信息 e.data。消息函数可以获得出发节点和目标节点的特征信息，描述了需要发给目标节点做下一步计算的信息。

#定义message函数，它将每个节点的PageRank值除以其out-degree，并将结果作为消息传递给它的邻居：
def pagerank_message_func(edges):
    return {'pv' : edges.src['pv'] / edges.src['deg']}

在DGL中，消息函数表示为Edge UDF。边UDF采用单个参数边。它有三个成员src，dst和data，分别用于访问源节点特征，目标节点特征和边特征。此处，该函数仅从源节点功能计算消息。

 

接下来，我们定义reduce函数，它从mailbox中删除并聚合message，并计算其新的PageRank值：

#定义reduce函数，它从mailbox中删除并聚合message，并计算其新的PageRank值：
def pagerank_reduce_func(nodes):
    msgs = torch.sum(nodes.mailbox['pv'], dim=1)
    pv = (1 - DAMP) / N + DAMP * msgs
    return {'pv' : pv}

reduce函数是Node UDF。 节点UDF具有单个参数节点，其具有两个成员data和mailbox。 data包含节点特征，而mailbox包含沿第二维堆叠的所有传入message特征（因此dim = 1参数）。

可以结合这两张示意理解： 

消息UDF适用于一批边，而reduce UDF适用于一批边，但输出一批节点。 它们的关系如下：

 

我们定义了message函数和reduce函数，稍后将由DGL调用。

g.register_message_func(pagerank_message_func)
g.register_reduce_func(pagerank_reduce_func)

该算法非常简单。 以下是一个PageRank迭代的代码：

def pagerank_naive(g):
    # Phase #1: 沿所有边缘发送消息。
    for u, v in zip(*g.edges()):
        g.send((u, v))
    # Phase #2: 接收消息以计算新的PageRank值。
    for v in g.nodes():
        g.recv(v)

 2.3 Improvement with batching semantics  批处理语义的改进

上面的代码不会扩展到大图，因为它遍历所有节点。 DGL通过让用户在一批节点或边上进行计算来解决这个问题。 例如，以下代码一次触发多个节点和边上的message和reduce函数。

def pagerank_batch(g):
    g.send(g.edges())
    g.recv(g.nodes())

请注意，我们仍在使用相同的reduce函数pagerank_reduce_func，其中nodes.mailbox ['pv']是单张量，沿第二维堆叠传入的消息。

当然，人们会想知道是否甚至可以并行地对所有节点执行reduce，因为每个节点可能具有不同数量的传入消息，并且实际上不能将不同长度的张量“堆叠”在一起。通常，DGL通过将传入消息的数量分组，并为每个组调用reduce函数来解决问题。

  2.4 More improvement with higher level APIs  使用更高级别的API进行更多改进

DGL提供了许多以各种方式组合基本send和recv的例程。它们被称为level-2 APIs(二级-API)。例如，PageRank示例可以进一步简化如下：

#定义PageRank示例的二级—API（消息传递）
def pagerank_level2(g):
    g.update_all()

除了update_all之外，我们还在此二级类别中有pull，push和send_and_recv。有关更多详细信息，请参阅API参考。

  2.5 Even more improvement with DGL builtin functions 使用DGL内置函数进一步改进

由于一些message和reduce函数非常常用，DGL还提供了内置函数。例如，可以在PageRank示例中使用两个内置函数：

    dgl.function.copy_src（src，out）是一个边UDF，它使用源节点特征数据计算输出。用户需要指定源特征数据（src）的名称和输出名称（out）。

    dgl.function.sum（msg，out）是一个节点UDF，它对节点邮箱中的消息进行求和。用户需要指定消息名称（msg）和输出名称（out）。

例如，PageRank示例可以重写如下：

#调用dgl内置函数
import dgl.function as fn

def pagerank_builtin(g):  #并行更新
    g.ndata['pv'] = g.ndata['pv'] / g.ndata['deg']
    g.update_all(message_func=fn.copy_src(src='pv', out='m'),
                 reduce_func=fn.sum(msg='m',out='m_sum'))
    g.ndata['pv'] = (1 - DAMP) / N + DAMP * g.ndata['m_sum']

在这里，我们直接提供UDFs作为update_all的参数。这将覆盖以前的UDFs。

除了简化代码之外，使用内置函数还使DGL有机会将操作融合在一起，从而加快执行速度。例如，DGL将copy_src message函数和sum reduce函数融合为一个稀疏矩阵向量（spMV）乘法。

本节描述了为什么spMV可以加速PageRank中的分散 - 聚集阶段。有关DGL中内置函数的更多详细信息，请阅读API参考。

您还可以下载并运行代码以感受其中的差异：

for k in range(K):
    #取消注释相应的行以选择不同的版本。
    # pagerank_naive(g)
    # pagerank_batch(g)
    # pagerank_level2(g)
    pagerank_builtin(g)
print(g.ndata['pv'])

out：

tensor([0.0101, 0.0084, 0.0134, 0.0092, 0.0090, 0.0132, 0.0075, 0.0113, 0.0116,
        0.0092, 0.0112, 0.0113, 0.0101, 0.0074, 0.0093, 0.0111, 0.0078, 0.0136,
        0.0083, 0.0067, 0.0084, 0.0094, 0.0088, 0.0066, 0.0136, 0.0112, 0.0067,
        0.0067, 0.0102, 0.0059, 0.0136, 0.0111, 0.0087, 0.0126, 0.0076, 0.0091,
        0.0125, 0.0125, 0.0058, 0.0092, 0.0113, 0.0082, 0.0153, 0.0084, 0.0075,
        0.0093, 0.0066, 0.0092, 0.0092, 0.0109, 0.0103, 0.0110, 0.0059, 0.0101,
        0.0110, 0.0125, 0.0126, 0.0084, 0.0105, 0.0067, 0.0143, 0.0125, 0.0118,
        0.0102, 0.0102, 0.0076, 0.0093, 0.0075, 0.0118, 0.0068, 0.0118, 0.0067,
        0.0068, 0.0101, 0.0097, 0.0076, 0.0156, 0.0084, 0.0093, 0.0099, 0.0109,
        0.0143, 0.0060, 0.0113, 0.0083, 0.0159, 0.0105, 0.0150, 0.0075, 0.0110,
        0.0069, 0.0108, 0.0076, 0.0132, 0.0126, 0.0065, 0.0112, 0.0143, 0.0111,
        0.0128])

for k in range(K):
    #取消注释相应的行以选择不同的版本。
    # pagerank_naive(g)
    # pagerank_batch(g)
     pagerank_level2(g)
   #pagerank_builtin(g)
print(g.ndata['pv'])

out：

tensor([0.0052, 0.0094, 0.0119, 0.0080, 0.0068, 0.0088, 0.0068, 0.0104, 0.0076,
        0.0061, 0.0106, 0.0084, 0.0086, 0.0104, 0.0061, 0.0060, 0.0060, 0.0061,
        0.0069, 0.0149, 0.0086, 0.0080, 0.0156, 0.0141, 0.0103, 0.0076, 0.0086,
        0.0084, 0.0104, 0.0058, 0.0085, 0.0052, 0.0097, 0.0122, 0.0096, 0.0110,
        0.0094, 0.0079, 0.0104, 0.0107, 0.0106, 0.0103, 0.0111, 0.0141, 0.0145,
        0.0131, 0.0095, 0.0093, 0.0148, 0.0120, 0.0093, 0.0101, 0.0120, 0.0102,
        0.0119, 0.0076, 0.0085, 0.0079, 0.0076, 0.0112, 0.0119, 0.0085, 0.0166,
        0.0135, 0.0140, 0.0128, 0.0094, 0.0075, 0.0085, 0.0068, 0.0121, 0.0094,
        0.0094, 0.0133, 0.0103, 0.0164, 0.0117, 0.0053, 0.0122, 0.0061, 0.0096,
        0.0063, 0.0150, 0.0120, 0.0139, 0.0148, 0.0093, 0.0086, 0.0076, 0.0112,
        0.0112, 0.0141, 0.0118, 0.0096, 0.0118, 0.0083, 0.0104, 0.0087, 0.0085,
        0.0093])

for k in range(K):
    #取消注释相应的行以选择不同的版本。
    # pagerank_naive(g)
     pagerank_batch(g)
    # pagerank_level2(g)
   #pagerank_builtin(g)
print(g.ndata['pv'])

out：

tensor([0.0052, 0.0094, 0.0119, 0.0080, 0.0068, 0.0088, 0.0068, 0.0104, 0.0076,
        0.0061, 0.0106, 0.0084, 0.0086, 0.0104, 0.0061, 0.0060, 0.0060, 0.0061,
        0.0069, 0.0149, 0.0086, 0.0080, 0.0156, 0.0141, 0.0103, 0.0076, 0.0086,
        0.0084, 0.0104, 0.0058, 0.0085, 0.0052, 0.0097, 0.0122, 0.0096, 0.0110,
        0.0094, 0.0079, 0.0104, 0.0107, 0.0106, 0.0103, 0.0111, 0.0141, 0.0145,
        0.0131, 0.0095, 0.0093, 0.0148, 0.0120, 0.0093, 0.0101, 0.0120, 0.0102,
        0.0119, 0.0076, 0.0085, 0.0079, 0.0076, 0.0112, 0.0119, 0.0085, 0.0166,
        0.0135, 0.0140, 0.0128, 0.0094, 0.0075, 0.0085, 0.0068, 0.0121, 0.0094,
        0.0094, 0.0133, 0.0103, 0.0164, 0.0117, 0.0053, 0.0122, 0.0061, 0.0096,
        0.0063, 0.0150, 0.0120, 0.0139, 0.0148, 0.0093, 0.0086, 0.0076, 0.0112,
        0.0112, 0.0141, 0.0118, 0.0096, 0.0118, 0.0083, 0.0104, 0.0087, 0.0085,
        0.0093])

for k in range(K):
    #取消注释相应的行以选择不同的版本。
     pagerank_naive(g)
    # pagerank_batch(g)
    # pagerank_level2(g)
   #pagerank_builtin(g)
print(g.ndata['pv'])

out：

tensor([0.0084, 0.0116, 0.0067, 0.0109, 0.0091, 0.0070, 0.0085, 0.0092, 0.0092,
        0.0103, 0.0049, 0.0110, 0.0150, 0.0092, 0.0091, 0.0142, 0.0058, 0.0101,
        0.0067, 0.0095, 0.0124, 0.0125, 0.0099, 0.0111, 0.0109, 0.0136, 0.0118,
        0.0099, 0.0101, 0.0059, 0.0069, 0.0118, 0.0123, 0.0093, 0.0083, 0.0103,
        0.0101, 0.0075, 0.0117, 0.0126, 0.0092, 0.0143, 0.0136, 0.0074, 0.0093,
        0.0075, 0.0142, 0.0075, 0.0102, 0.0066, 0.0084, 0.0120, 0.0125, 0.0084,
        0.0085, 0.0091, 0.0092, 0.0100, 0.0105, 0.0109, 0.0124, 0.0134, 0.0101,
        0.0092, 0.0073, 0.0141, 0.0128, 0.0075, 0.0083, 0.0057, 0.0085, 0.0060,
        0.0092, 0.0101, 0.0127, 0.0067, 0.0134, 0.0082, 0.0076, 0.0099, 0.0135,
        0.0103, 0.0090, 0.0132, 0.0127, 0.0101, 0.0164, 0.0098, 0.0091, 0.0125,
        0.0085, 0.0084, 0.0084, 0.0116, 0.0075, 0.0082, 0.0118, 0.0085, 0.0108,
        0.0116])

 

2.6 将spMV用于PageRank

使用内置函数允许DGL理解UDF的语义，从而为您提供更高效的实现。例如，在PageRank的情况下，加速它的一个常见技巧是使用其线性代数形式。

这里，Rk 是在迭代k 处所有节点的PageRank值的向量;  A是图的稀疏邻接矩阵。计算该等式非常有效，因为存在用于稀疏矩阵向量乘法（spMV）的高效GPU内核。DGL通过内置函数检测是否可以进行此类优化。如果内置的某些组合可以映射到spMV内核（例如pagerank示例），DGL将自动使用它。因此，我们建议尽可能使用内置函数。

2.7 Next steps

现在是时候转向DGL中的一些真实模型了。

查看所有模型教程的概述页面。
想了解更多关于图形神经网络的知识吗？从GCN教程开始。
想知道DGL如何批量多个图表？从TreeLSTM教程开始。
想玩一些图形生成模型吗？从我们的深度生成图模型教程开始。
想看看传统模型是如何在图形视图中解释的？查看我们关于CapsuleNet和Transformer的教程。