LSTM原理及实现（一）

LSTM原理及实现

RNN

LSTM

实现

RNN基本原理

前言

当我们处理与事件发生的时间轴有关系的问题时，比如自然语言处理，文本处理，文字的上下文是有一定的关联性的；时间序列数据，如连续几天的天气状况，当日的天气情况与过去的几天有某些联系；又比如语音识别，机器翻译等。在考虑这些和时间轴相关的问题时，传统的神经网络就无能为力了，因此就有了RNN（recurrent neural network，循环神经网络），了解RNN先了解DNN基本原理。同样这里介绍RNN基本原理，也是为了铺垫我们的重点LSTM网络（long short term memory，长短时记忆神经网络）。

定义

递归神经网络（RNN）是两种人工神经网络的总称。一种是时间递归神经网络（recurrent neural network），另一种是结构递归神经网络（recursive neural network）。时间递归神经网络的神经元间连接构成矩阵，而结构递归神经网络利用相似的神经网络结构递归构造更为复杂的深度网络。RNN一般指代时间递归神经网络。

网络结构

图1.DNN基础结构

对于这样一个DNN正向传播的基础结构来说，我们的整个过程就是，将输入x与权重矩阵w结合，以wx + b的形式输入隐藏层（Layer L2），经过激活函数f(x)的处理，得到输出结果a1, a2, a3， 然后与对应的权重、偏置结合，作为输出层（Layer L3）的输入，经过激活函数，得到最终输出结果。

图2.RNN基础结构

KaTeX parse error: No such environment: equation at position 8: \begin{̲e̲q̲u̲a̲t̲i̲o̲n̲}̲ \begin{split} …

其中$g_1$常用tanh和Relu激活函数，$g_2$常用sigmoid或者softmax.

BP

循环神经网络的训练类似于传统神经网络的训练。我们也使用反向传播算法，但是有所变化。因为循环神经网络在所有时刻的参数是共享的，但是每个输出的梯度不仅依赖当前时刻的计算，还依赖之前时刻的计算。例如，为了计算时刻 t = 4 的梯度，我们还需要反向传播3步，然后将梯度相加。这个被称为Backpropagation Through Time（BPTT）。

这与我们在深度前馈神经网络中使用的标准反向传播算法基本相同。主要的差异就是我们将每时刻 W 的梯度相加。在传统的神经网络中，我们在层之间并没有共享参数，所以我们不需要相加。

反向传播基本和DNN中BP算法一致，这里不做赘述了，从${\hat{y}}^{t>}$与真实值$y^{<t>}$做损失函数计算，所有RNN-cellde 损失函数做成本函数计算，以此为目标函数，基于最优化方法，常用梯度下降法进行目标优化，从而最终得到我们的最终结果。

小结

RNN 的关键点之一就是他们可以用来连接先前的信息到当前的任务上，例如使用过去的视频段来推测对当前段的理解。但是当相关信息和当前预测位置之间的间隔变得非常大，RNN 会丧失学习到连接如此远的信息的能力。我们仅仅需要明白的是利用BPTT算法训练出来的普通循环神经网络很难学习长期依赖（例如，距离很远的两步之间的依赖），原因就在于梯度消失/发散问题。但是RNN 绝对可以处理这样的长期依赖问题，人们可以仔细挑选参数来解决这类问题中的最初级形式，但在实践中，RNN 肯定不能够成功学习到这些知识。训练和参数设计十分复杂。LSTM就是专门设计出来解决这个问题的。

LSTM

LSTM网络

long short term memory，即我们所称呼的LSTM，是为了解决长期以来问题而专门设计出来的，所有的RNN都具有一种重复神经网络模块的链式形式。在标准RNN中，这个重复的结构模块只有一个非常简单的结构，例如一个tanh层。

图3.RNNcell

LSTM 同样是这样的结构，但是重复的模块拥有一个不同的结构。不同于单一神经网络层，这里是有四个，以一种非常特殊的方式进行交互。

图4.LSTMcell

LSTM核心思想

LSTM的关键在于细胞的状态整个(绿色的图表示的是一个cell)，和穿过细胞的那条水平线。

细胞状态类似于传送带。直接在整个链上运行，只有一些少量的线性交互。信息在上面流传保持不变会很容易。

图5.LSTMcell内部结构图

若只有上面的那条水平线是没办法实现添加或者删除信息的。而是通过一种叫做 门（gates） 的结构来实现的。

门 可以实现选择性地让信息通过，主要是通过一个 sigmoid 的神经层 和一个逐点相乘的操作来实现的。

图6.信息节点

sigmoid 层输出（是一个向量）的每个元素都是一个在 0 和 1 之间的实数，表示让对应信息通过的权重（或者占比）。比如， 0 表示“不让任何信息通过”， 1 表示“让所有信息通过”。

LSTM通过三个这样的基本结构来实现信息的保护和控制。这三个门分别输入门、遗忘门和输出门。

深入理解LSTM

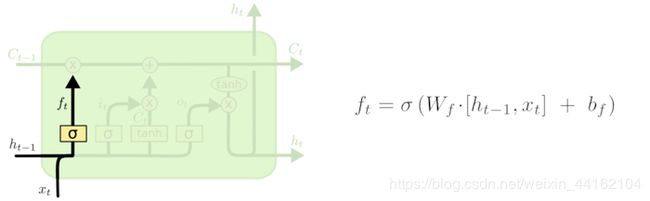
遗忘门

在我们 LSTM 中的第一步是决定我们会从细胞状态中丢弃什么信息。这个决定通过一个称为忘记门层完成。该门会读取$h_{t-1}$和$x_t$，输出一个在 0到 1之间的数值给每个在细胞状态$C_{t-1}$中的数字。1 表示“完全保留”，0 表示“完全舍弃”。

其中ht−1表示的是上一个cell的输出，xt表示的是当前细胞的输入。σσ表示sigmod函数。

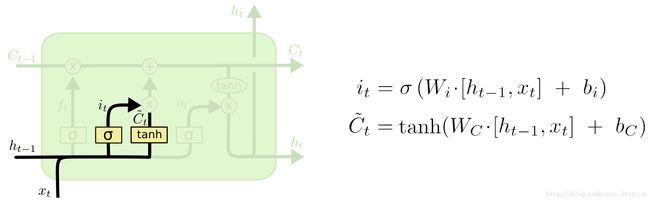
输入门

下一步是决定让多少新的信息加入到 cell 状态 中来。实现这个需要包括两个 步骤：首先，一个叫做“input gate layer ”的 sigmoid 层决定哪些信息需要更新；一个 tanh 层生成一个向量，也就是备选的用来更新的内容，C^t 。在下一步，我们把这两部分联合起来，对 cell 的状态进行一个更新。

现在是更新旧细胞状态的时间了，Ct−1更新为Ct。前面的步骤已经决定了将会做什么，我们现在就是实际去完成。

我们把旧状态与ft相乘，丢弃掉我们确定需要丢弃的信息。接着加上it∗C~t。这就是新的候选值，根据我们决定更新每个状态的程度进行变化。

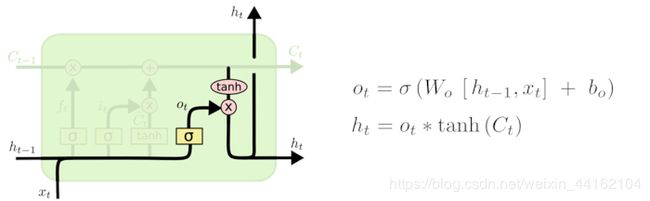
输出门

最终，我们需要确定输出什么值。这个输出将会基于我们的细胞状态，但是也是一个过滤后的版本。首先，我们运行一个 sigmoid 层来确定细胞状态的哪个部分将输出出去。接着，我们把细胞状态通过 tanh 进行处理（得到一个在 -1 到 1 之间的值）并将它和 sigmoid 门的输出相乘，最终我们仅仅会输出我们确定输出的那部分。

实现

keras.layers.LSTM(units, activation='tanh', recurrent_activation='hard_sigmoid', use_bias=True, kernel_initializer='glorot_uniform', recurrent_initializer='orthogonal', bias_initializer='zeros', unit_forget_bias=True, kernel_regularizer=None, recurrent_regularizer=None, bias_regularizer=None, activity_regularizer=None, kernel_constraint=None, recurrent_constraint=None, bias_constraint=None, dropout=0.0, recurrent_dropout=0.0, implementation=1, return_sequences=False, return_state=False, go_backwards=False, stateful=False, unroll=False)

长短期记忆网络层（Long Short-Term Memory） - Hochreiter 1997.

参数

• units: 正整数，输出空间的维度。
• activation: 要使用的激活函数 (详见 activations)。 如果传入 None，则不使用激活函数 (即 线性激活：a(x) = x)。
• recurrent_activation: 用于循环时间步的激活函数 (详见 activations)。 默认：分段线性近似 sigmoid (hard_sigmoid)。 如果传入 None，则不使用激活函数 (即 线性激活：a(x) = x)。
• use_bias: 布尔值，该层是否使用偏置向量。
• kernel_initializer: kernel 权值矩阵的初始化器， 用于输入的线性转换 (详见 initializers)。
• recurrent_initializer: recurrent_kernel 权值矩阵 的初始化器，用于循环层状态的线性转换 (详见 initializers)。
• bias_initializer:偏置向量的初始化器 (详见initializers).
• unit_forget_bias: 布尔值。 如果为 True，初始化时，将忘记门的偏置加 1。 将其设置为 True 同时还会强制 bias_initializer="zeros"。 这个建议来自 Jozefowicz et al.。
• kernel_regularizer: 运用到 kernel 权值矩阵的正则化函数 (详见 regularizer)。
• recurrent_regularizer: 运用到 recurrent_kernel 权值矩阵的正则化函数 (详见 regularizer)。
• bias_regularizer: 运用到偏置向量的正则化函数 (详见 regularizer)。
• activity_regularizer: 运用到层输出（它的激活值）的正则化函数 (详见 regularizer)。
• kernel_constraint: 运用到 kernel 权值矩阵的约束函数 (详见 constraints)。
• recurrent_constraint: 运用到 recurrent_kernel 权值矩阵的约束函数 (详见 constraints)。
• bias_constraint: 运用到偏置向量的约束函数 (详见 constraints)。
• dropout: 在 0 和 1 之间的浮点数。 单元的丢弃比例，用于输入的线性转换。
• recurrent_dropout: 在 0 和 1 之间的浮点数。 单元的丢弃比例，用于循环层状态的线性转换。
• implementation: 实现模式，1 或 2。 模式 1 将把它的操作结构化为更多的小的点积和加法操作， 而模式 2 将把它们分批到更少，更大的操作中。 这些模式在不同的硬件和不同的应用中具有不同的性能配置文件。
• return_sequences: 布尔值。是返回输出序列中的最后一个输出，还是全部序列。
• return_state: 布尔值。除了输出之外是否返回最后一个状态。
• go_backwards: 布尔值 (默认 False)。 如果为 True，则向后处理输入序列并返回相反的序列。
• stateful: 布尔值 (默认 False)。 如果为 True，则批次中索引 i 处的每个样品的最后状态 将用作下一批次中索引 i 样品的初始状态。
• unroll: 布尔值 (默认 False)。 如果为 True，则网络将展开，否则将使用符号循环。 展开可以加速 RNN，但它往往会占用更多的内存。 展开只适用于短序列。

参考资料

吴恩达深度学习系列课程

https://tensorflow.google.cn/guide/keras#sequential_model

https://keras.io/zh/layers/recurrent/