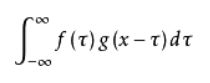计算机视觉及OpenCV入门简介

计算机视觉及OpenCV入门简介

这是一篇实验室培训过后写的感悟，附带授课大佬及实验室GitHub地址：

• 大佬：https://github.com/shentibeitaokongle
• 实验室：https://github.com/android-nuc

计算机视觉

什么是计算机视觉？

计算机视觉是指用摄影机和电脑代替人眼对目标进行识别、跟踪和测量等机器视觉，并进一步做图形处理，使电脑处理成为更适合人眼观察或传送给仪器检测的图像。

简单概括为：

1. 让计算机去认知世界，人工智能
2. 图像处理 + 机器学习 + 三维理论

计算机视觉能干什么？

• 图像识别
• 无人汽车
• AR、VR
• 三维重建
• 工程测绘
• 图像分割
• ……

计算机视觉(CV)与计算机图形学(CG)的区别

计算机图形学（Computer Graphics）和计算机视觉（Computer Vision）是同一过程的两个方向。CG将抽象的语义信息转化成图像，而CV是从图像中提取抽象的语义信息。

计算机图形学：输入的是对虚拟场景的描述，通常为多边形数组，而每个多边形由三个顶点组成，每个顶点包括三维坐标、贴图坐标、RGB颜色等。输出的是图像，即二维像素数组。

计算机视觉：输入的是图像或图像序列，通常来自相机、摄像头或视频文件。输出的是对于图像序列对应的真实世界的理解，比如检测人脸、识别车牌。

参考文章：https://blog.csdn.net/hanlin_tan/article/details/50447895

CV对大学生比赛、就业、读研有什么用？

• CV的魅力在于各种高深的研究方向和算法，有广泛的应用场景，结合CV会有很多有趣的idea
• 图像处理，或者视觉相关的岗位薪资比较高
• 计算机视觉仍然是计算机科研的热门方向

OpenCV

下面是对OpenCV的简单介绍，应用实例在后面。

什么是OpenCV？

中文名：开源计算机视觉库
英文全称：Open Source Computer Vision Library

OpenCV于1999年由Intel建立，如今由Willow Garage提供支持。OpenCV是一个基于BSD许可（开源）发行的跨平台计算机视觉库，可以运行在Linux、Windows和Mac OS操作系统上。它由一系列 C 函数和少量 C++ 类构成，同时提供了Python、Ruby、MATLAB等语言的接口，实现了图像处理和计算机视觉方面的很多通用算法。它支持CUDA加速，现在已经发展到了OpenCV4.0.1版本。

为什么会有OpenCV？

计算机视觉市场巨大而且持续增长，且这方面没有标准API，如今的计算机视觉软件大概有以下三种：
1、研究代码（慢，不稳定，独立并与其他库不兼容）
2、耗费很高的商业化工具（比如Halcon, MATLAB+Simulink）
3、依赖硬件的一些特别的解决方案（比如视频监控，制造控制系统，医疗设备）这是如今的现状，而标准的API将简化计算机视觉程序和解决方案的开发，OpenCV致力于成为这样的标准API。
OpenCV致力于真实世界的实时应用，通过优化的C代码的编写对其执行速度带来了可观的提升，并且可以通过购买Intel的IPP高性能多媒体函数库（Integrated Performance Primitives）得到更快的处理速度。

图像

图像的取样与量化

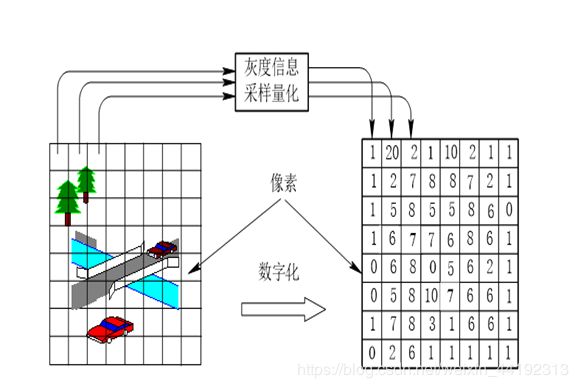
计算机保存的图像都是一个一个的像素点，称为数字图像。我们想要在计算机中处理图像，就必须把真实的图像通过数字化转变成计算机能够接受的显示和存储格式，然后再用计算机进行分析处理。
图像数字化过程由图像的取样与量化来完成。取样就是要用多少点来描述一幅图像，取样结果质量的高低就是用图像的分辨率来衡量的；量化是指要使用多大范围的数值来表示图像采样之后的一个点。也可以说，数字化坐标值称为取样，数字化幅度值称为量化。

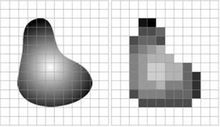
上图左侧是要数字化的物体，右侧是数字化后的图像，每个小格即为一个像素点。


推荐文章：https://www.cnblogs.com/yunfung/p/6753337.html
https://blog.csdn.net/zqhwando/article/details/78871140

图像还能看成是什么？

图像由一组波组成，我们要把图像进行数字化存储，就需要提到一个概念——傅里叶级数。

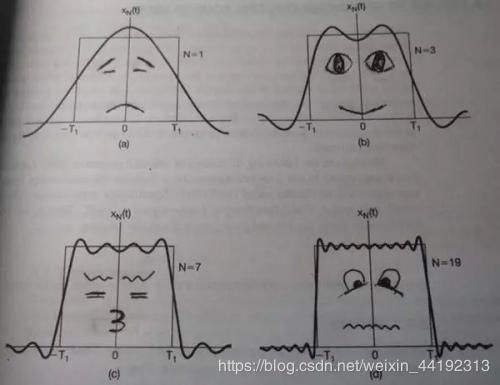
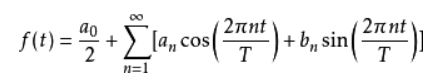
傅里叶级数指任何周期函数都可以用正弦函数和余弦函数构成的无穷级数来表示。

傅里叶变换（空间域->频率域）

傅立叶变换，表示能将满足一定条件的某个函数表示成三角函数（正弦和/或余弦函数）或者它们的积分的线性组合。
傅里叶变换的本质是将一个周期信号分解成无限多分开的（离散的）正弦波。

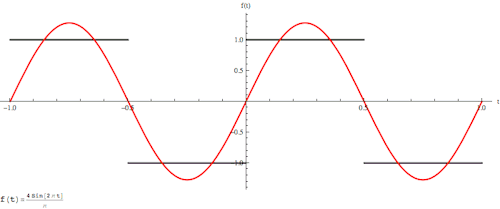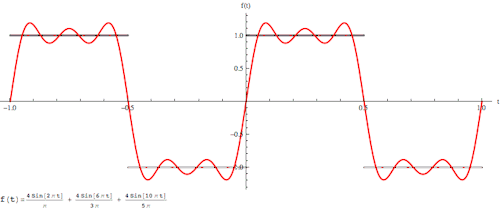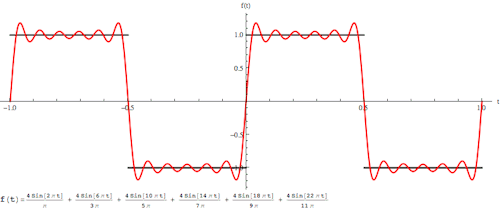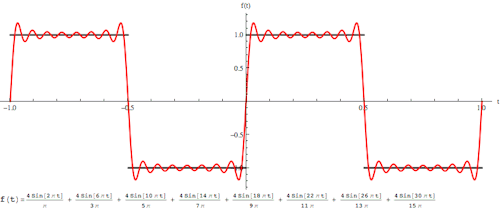
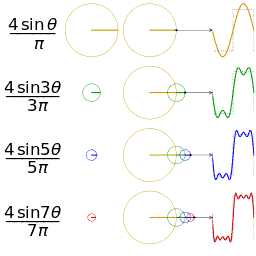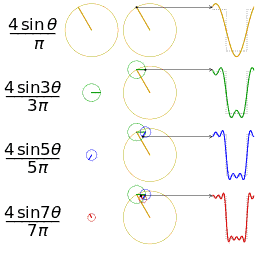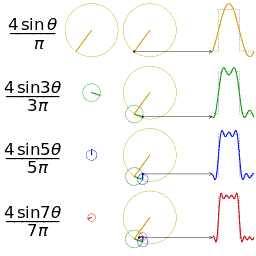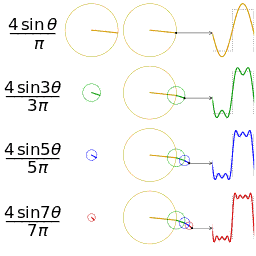
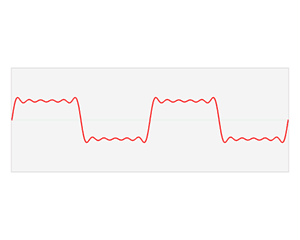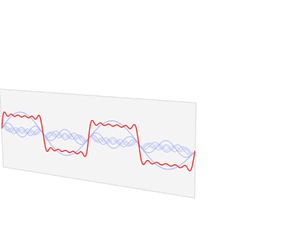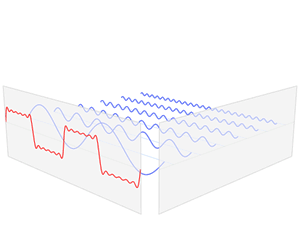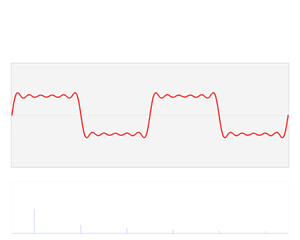
为什么要提到傅里叶变换呢？因为当你在二维很难处理一个图像的时候，可能换个“角度”处理起来却很简单，这是傅里叶变换的一个魅力所在。

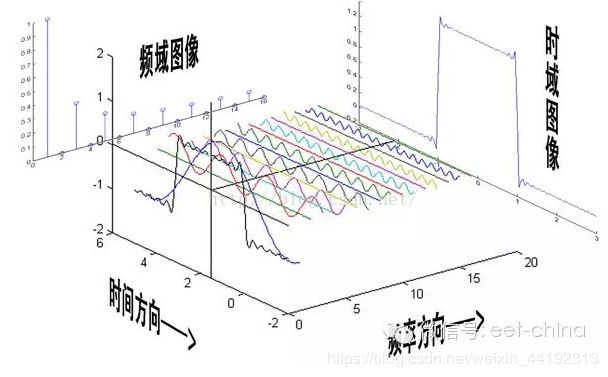
例如，处理一张异常图片，频率方向无法进行或者工作量太大时，可能改为在时间方向处理会很简单。

参考文章：https://blog.csdn.net/yangdashi888/article/details/53215256

图像滤波（空间域滤波）

图像滤波，即在尽量保留图像细节特征的条件下对目标图像的噪声进行抑制，是图像预处理中不可缺少的操作，其处理效果的好坏将直接影响到后续图像处理和分析的有效性和可靠性。其实质是减少数字图像在使用前的的噪声污染。

线性滤波可以说是图像处理最基本的方法，它可以允许我们对图像进行处理，产生很多不同的效果。做法很简单。首先，我们有一个二维的滤波器矩阵（有个高大上的名字叫卷积核or滤波器）和一个要处理的二维图像。然后，对于图像的每一个像素点，计算它的邻域像素和滤波器矩阵的对应元素的乘积，然后加起来，作为该像素位置的值。这样就完成了滤波过程。

卷积

卷积可以看作是一种结合了矩阵运算的计算方法，它是是分析数学中一种重要的运算。

设:f(x),g(x)是R1上的两个可积函数，作积分：

可以证明，关于几乎所有的实数x，上述积分是存在的。这样，随着x的不同取值，这个积分就定义了一个新函数 h(x)，称为函数 f 与 g 的卷积，记为 h(x) = (f * g)(x)。

容易验证，(f * g)(x) = (g * f)(x)，并且(f * g)(x)仍为可积函数。

卷积与傅里叶变换有着密切的关系。利用一点性质，即两函数的傅里叶变换的乘积等于它们卷积后的傅里叶变换，能使傅里叶分析中许多问题的处理得到简化。

卷积关系最重要的一种情况，就是在信号与线性系统或数字信号处理中的卷积定理。利用该定理，可以将时间域或空间域中的卷积运算等价为频率域的相乘运算，从而利用FFT等快速算法，实现有效的计算，节省运算代价。

C++语言代码：

void convolution(float *input1, float *input2, float *output, int mm, int nn)
{ 
    float *xx = new float[mm+nn-1]; 
    // do convolution 
    for (int i = 0; i < mm+nn-1; i++)
    { 
        xx[i] = 0.0;
        for (int j = 0; j < mm; j++) 
        { 
            if (i-j > 0 && i-j < nn)
            xx[i] += input1[j] * input2[i-j]; 
        } 
     }
     // set value to the output array 
     for (int i = 0; i < mm; i++) 
     output[i] = xx[i + (nn-1) / 2];
     delete[] xx;
}

示例：

• 原图
  

• 黑白
  

    VideoCapture video(0);
	Mat src = imread("F:/C/picture/lena.JPG", 1);
	cvtColor(src, src, COLOR_BGR2GRAY);
	namedWindow("src", WINDOW_AUTOSIZE);
	imshow("src", src);

• 卷积核 or 滤波器：[ -1, 0, 1 ]

    VideoCapture video(0);
	Mat src = imread("F:/C/picture/lena.JPG", 1);
	cvtColor(src, src, COLOR_BGR2GRAY);
	namedWindow("src", WINDOW_AUTOSIZE);
	imshow("src", src);

	Mat dImg = Mat(src.rows, src.cols - 2, CV_8UC1);
	for (int i = 0; i < src.rows; i++)
	{
		for (int j = 1; j < src.cols - 1; j++)
		{
			dImg.at<uchar>(i, j - 1) = src.at<uchar>(i, j + 1) - src.at<uchar>(i, j - 1);
		}
	}
	namedWindow("dst", CV_WINDOW_AUTOSIZE);
	imshow("dst", dImg);
	waitKey(0);

另附卷积与相关的区别：https://blog.csdn.net/m0_37407756/article/details/78593917

高斯模糊

高斯模糊，也叫高斯平滑，用来减少图像噪声以及降低细节层次。从数学的角度来看，图像的高斯模糊过程就是图像与正态分布做卷积。

可以将高斯模糊简单理解为图像中的每个像素都重新设置像素值为周边相邻像素的平均值，相邻像素的范围越大，模糊程度就越大。需要注意的是，高斯模糊应该使用加权平均，因为距离当前像素越近的像素与其联系越密切。

由于正态分布又叫作高斯分布，所以这项技术就叫作高斯模糊。由于高斯函数的傅立叶变换是另外一个高斯函数，所以高斯模糊对于图像来说就是一个低通滤波器。

还是用前面的黑白图片做示范：

代码：

    //5x5卷积模板
	Mat model = Mat(5, 5, CV_64FC1);
	
	double sigma = 80;
	for (int i = -2; i <= 2; i++)
	{
		for (int j = -2; j <= 2; j++)
		{
			model.at<double>(i + 2, j + 2) = 
				exp(-(i * i + j * j) / (2 * sigma * sigma)) / (2 * PI * sigma * sigma);
		}
	}

	double gaussSum = 0;
	gaussSum = sum(model).val[0];
	for (int i = 0; i < model.rows; i++)
	{
		for (int j = 0; j < 5; j++)
		{
			model.at<double>(i, j) = model.at<double>(i, j) / gaussSum;
		}
	}

	Mat dst = Mat(src.rows - 4, src.cols - 4, CV_8UC1);

	for (int i = 2; i < src.rows - 2; i++)
	{
		for (int j = 2; j < src.cols - 2; j++)
		{
			double sum = 0;
			for (int m = 0; m < model.rows; m++)
			{
				for (int n = 0;n < model.cols; n++)
				{
					sum += (double)src.at<uchar>(i + m - 2, j + n - 2) * model.at<double>(m, n);
				}
			}

			dst.at<uchar>(i - 2, j - 2) = (uchar)sum;

		}
	}

	namedWindow("gaussBlur", WINDOW_AUTOSIZE);
	imshow("gaussBlur", dst);

	waitKey(0);

正态分布

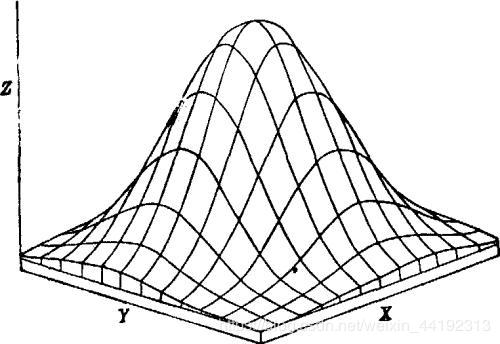
参考文章：https://blog.csdn.net/zouxy09/article/details/49080029

滤波常用API

• 边缘检测（微分）
• Sobel算子，拉普拉斯算子
• 图像去噪/平滑（积分）
• GaussianBlur（高斯模糊）

相关会议及期刊

以下是收集的一些与计算机视觉相关的会议及期刊，感兴趣的话可以看看：

会议

• 顶级
  ICCV：International Conference on Computer Vision，国际计算机视觉大会
  2019官网：http://iccv2019.thecvf.com/
  CVPR：International Conference on Computer Vision and Pattern Recognition，国际计算机视觉与模式识别大会
  2019官网：http://cvpr2019.thecvf.com/
  ECCV：European Conference on Computer Vision，欧洲计算机视觉大会
  2018官网：https://eccv2018.org/
• 较好
  ICIP：International Conference on Image Processing，国际图像处理大会
  BMVC：British Machine Vision Conference，英国机器视觉大会
  ICPR：International Conference on Pattern Recognition，国际模式识别大会
  ACCV：Asian Conference on Computer Vision，亚洲计算机视觉大会

期刊

• 顶级
  PAMI：IEEE Transactions on Pattern Analysis and Machine Intelligence，IEEE 模式分析与机器智能杂志
  官网：https://ieeexplore.ieee.org/Xplore/home.jsp
  IJCV：International Journal on Computer Vision，国际计算机视觉杂志
  官网：https://lmb.informatik.uni-freiburg.de/index.php
• 较好
  TIP:IEEE Transactions on Image Processing，IEEE图像处理杂志
  CVIU：Computer Vision and Image Understanding，计算机视觉与图像理解
  PR：Pattern Recognition，模式识别
  PRL：Pattern Recognition Letters，模式识别快报