初学机器学习总结(梯度下降)
初学机器学习总结及梯度下降
- 初学机器学习总结
- 认识机器学习
- 机器学习分类
- 在监督学习方面
- 无监督学习方面
- 机器学习流程
- 机器学习方法三要素
- 梯度下降算法
- 1.如何理解梯度?
- 2.线性回归中的梯度下降算法
- 3.梯度下降算法的变形形式
- 1.批量梯度下降算法—BGD
- 2.随机梯度下降算法—SGD
- 3.小批量梯度下降算法—MBGD
- 4.梯度下降算法调优
初学机器学习总结
认识机器学习
机器学习(MACHINE LEARNING),有时简称为ML。
今天初学机器学习,对什么是机器学习做出了如下定义:
为了解决任务T,设计一段程序,从经验E中学习,达到性能度量值P,当且仅当有了经验E后,经过P评判,程序在处理T时的性能得到提升。
机器学习分类
机器学习分为三类:
{ 有 监 督 学 习 ( 带 标 签 ) : 回 归 、 分 类 无 监 督 学 习 ( 无 标 签 ) : 聚 类 、 降 维 强 化 学 习 : 有 模 型 学 习 、 无 模 型 学 习 \left\{ \begin{array}{c} 有监督学习(带标签):回归、分类 \\ 无监督学习(无标签):聚类、降维 \\ 强化学习:有模型学习、无模型学习\end{array}\right. ⎩⎨⎧有监督学习(带标签):回归、分类无监督学习(无标签):聚类、降维强化学习:有模型学习、无模型学习
在监督学习方面
对两种不同的方法进行区别:
分类问题是指:样本标签属于离散变量
回归问题是指:样本标签属于连续变量
对于分类问题经常会使用两种模型:
1.生成模型(概率模型)
一般会采用联合概率分布和边缘概率分布去判别。
2.判别模型(非概率模型)
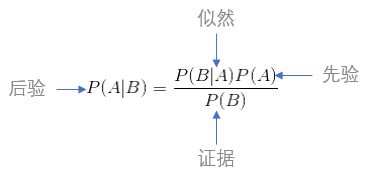
一般采用条件概率,也会由条件概率引出贝叶斯公式进行算法。
无监督学习方面
无监督学习指样本中不包含任何标签。
机器学习流程
1.特征表示
2.选择模型
3.训练模型
4.模型评估
机器学习方法三要素
1.模型
模型就是说我们将要学习的概率分布或者决策函数。
然后把所有的可能的条件概率或者决策函数放在一个集合里,这样的集合可以称之为假设空间。
2.策略
我们从假设空间中学习最优解的模型的方法,成为策略。
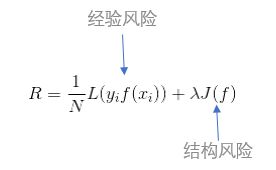
在实际中,预测值和真实值通常是不相等的,所以说在衡量这个模型到底是好与坏的情况下,引入了损失函数和风险函数来进行衡量。
用损失函数度量预测错误的程度,记作L(Y,f(x))
我们一般常用以下几种损失函数:
- 0-1损失函数
- 平方损失函数
- 绝对损失函数
- 对数损失函数(交叉熵损失函数)
3.算法
算法是指学习模型时的具体计算方法,求解最优模型归结为最优化问题。
在选择模型的时候尽量根据奥卡姆剃刀原理进行选择。
梯度下降算法
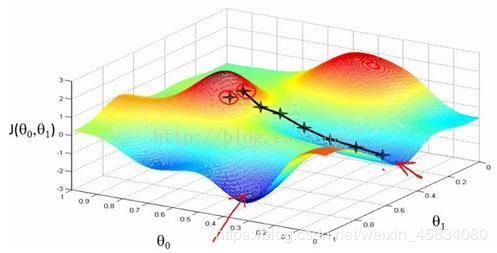
梯度下降算法的主要目的是通过迭代找到目标函数的最小值,或者收敛到最小值。
1.如何理解梯度?
在单变量中,就是对函数的微分。
在多变量中,则是求函数的偏导。
2.线性回归中的梯度下降算法
我们先假定一个h:
![]()
在上述式子中theta0和theta1都是未知参数,x是已知参数。
接下来我们只需求解损失函数的一阶导数,计算的代价比较小,这使得梯度下降法能在很多大规模数据集上得到应用。梯度下降法的含义是通过当前点的梯度方向寻找到新的迭代点。
损失函数为:
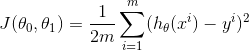
更新theta1的值为:
![]()
对于梯度下降法,关键在于求出损失函数的导数。
多变量的回归分析类似于单变量,利用偏导求损失函数。
构建一个多变量函数:

其中h:
![]()
对其求偏导得:
 基本思想
基本思想
3.梯度下降算法的变形形式
1.批量梯度下降算法—BGD
批量梯度下降法(Batch Gradient Descent)针对的是整个数据集,通过对所有的样本的计算来求解梯度的方向。
批量梯度下降法的损失函数为:

进一步得到批量梯度下降的迭代式为:
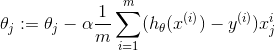
批量梯度迭代算法是对所有数据集进行更新,每迭代一次都要用到训练集中的所有数据,如果说样本很大,运行速度就会很慢!
优点:全局最优解;易于并行实现;
缺点:当样本数目很多时,训练过程会很慢,每次迭代需要耗费大量的时间。
但是从迭代次数上来看,BGD迭代的次数会相对比较少。
2.随机梯度下降算法—SGD
如果说数据特别多的时候,用BGD算法就不太合适,所以说我们可以引用随机梯度下降算法(Stochastic gradient descent)。
随机梯度下降算法是每次用一个数据来进行梯度下降。
随机梯度下降的迭代式为:
![]()
优点:它的训练速度非常之快。
缺点:
1.对于准确度来说,因为SGD每次训练仅采用一个样本决策梯度方向,可能得到局部最小值。如上图所示。
2.对于收敛速度来说,因为SGD每次迭代一个样本,就会导致迭代方向变化很大,不能很快的收敛到局部最优解。
3.小批量梯度下降算法—MBGD
小批量梯度算法(Stochastic gradient descent)是综合了BGD和SGD,每次迭代使用一个以上又不是全部的样本。
小批量梯度下降算法的迭代式为:
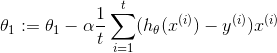
优点:使用多个样本相比SGD提高了梯度估计的精度。
缺点:同SGD一样,每次梯度估计的方向不能确定,可能需要很长时间才能接近最小值点,不会收敛。通常在使用MBGD之前先将数据集随机打乱,然后在划分Mini-bath,所以MGBD有时也称为SGD。
注意:
1.小批量梯度算法每次选择数据集的大小一般使用2的幂数,可以获得更少的运行时间。
2.遍历完所有数据,称为一个epoch,通常需要遍历几次epoch才行。
4.梯度下降算法调优
使用梯度下降算法求极值的时候,可以通过以下方法进行优化:
1.算法的步长。 可以多选一些值,从大到小,分别运行算法,看看迭代效果
- 如果说损失函数在变小,说明取值有效,否则要增大步长。
- 步长太长的话,会导致迭代过快,甚至有可能错过最优解。
- 步长太小的话,会导致迭代速度太慢,很长时间算法不能结束。
2.算法参数的初始值选择
- 初始值不同,获得的最小值有可能不同,所以说梯度下降求得的只是局部最小值。
- 如果损失函数是凸函数,则一定是最优解。
- 由于有局部最优解的风险,所以要需要多次用不同的初始值进行算法。
- 选择损失函数最小化的初值。
3.进行归一化
为了减少特征取值的影响,可以对特征数据标准化或者归一化。
标准化: ![]()
归一化:![]()
这样特征的新期望为0,新方差为1,所有特征梯度下降幅度想进,不会造成震荡。