定点数编码（详解补码）
在计算机中，定点数的编码主要有三种表示形式：原码、补码、移码。
一、原码是最容易理解的编码方式。用最高位表示正负，0 表示正数，1 表示负数。即设最高为位n，则符号位为 
。
| Decimal | Binary | Decimal | Binary | |
| 0 | 0000 | -0 | 1000 | |
| 1 | 0001 | -1 | 1001 | |
| 2 | 0010 | -2 | 1010 | |
| 3 | 0011 | -3 | 1011 | |
| 4 | 0100 | -4 | 1100 | |
| 5 | 0101 | -5 | 1101 | |
| 6 | 0110 | -6 | 1110 | |
| 7 | 0111 | -7 | 1111 |
显而易见地，用源码表示时，0 的表示不唯一，不利于程序员编程。另外，这种编码会导致加减运算方式无法统一，特别是当 a < b时，实现 a - b 比较困难，由于还要对额外的符号位进行处理，故不利于硬件的实现。
二、补码
相信各位对补码都不陌生，都知道补码的一条换算规则是：正数的补码和原码一样；负数的补码则是，符号位不变，其余位数取反，最后加一。但是为什么换算是这样的呢？补码到底是什么呢？为什么要用补码表示呢？
1. 先解释一下补码到底是什么。
补码的存在是依附于模运算系统的。在模运算系统中，一个数与它除以 “模” 后的余数等价。
例如我们生活中的时钟便是一种模 12 系统。
假定钟表时钟指向 10 ，要将它拨向 6 ，可以有两种方法
（1）逆时针拨动 4 格 ： 10 - 4 = 6
（2）顺时针拨动 8 格： 10 + 8 = 18 
6
在这个时钟的模 12 系统中 10 - 4 10 + 8 （mod 12） 也就是 -4 8 （mod 12）
则称 8 是 -4 对模 12 的补码（ -4 的模 12 补码等于 8），同样的 -3 9 （mod 12）
从这里我们可以得到 结论一：一个负数的补码等于模减去该负数的绝对值 （ 10 - |-4| = 10 - 4 ）
根据结论一，我们可以推出我们惯常使用的规则是怎么运算出来的了。看下面这个例子：
我想，现在小伙伴们应该知道我们平时使用的换算规则是怎么回事了。在这里，我还要推荐一个更简便的方法给大家：
从右到左遇到第一个 1 的前面各位取反。
还是上面 -123 这个例子好了。 -0111 1011 从右到左遇到的第一个 1 是 0 号位上的 1，因此，0 号位上的 1 不变，1~7号位上各位取反，得到 1000 0101
2. 在模运算系统中，为什么可以将减法运算统一成加法运算。
我们先用 “4 位 十进制” 模运算系统做例子。
从我们换算成补码的过程中就窥探出减法运算转化成加法运算的原因。当然，上面这个只是我自己的理解，如果小伙伴们有其他的理解一定要记得留言，因为我不清楚这个思路有没有错误。（/抱拳）
在计算机中，我们采用的是二进制，但是思想和做法都是相同的。例如
3. 为什么在计算机中大部分用补码表示数值呢？
因为计算机的运算器只有有限位，就像我们表示数值一样，一个byte 只有 8 位，超过 8 位就会溢出。假设为 n 位，那么运算结果只能保留低 n 位，即是一种模为 
的模运算系统。
4. 特殊数的补码
假定机器数有 n 位（例子中 n = 4)
5. 变形补码（ 4's comlement)
变形补码就是用两个符号位的补码，主要用于存放运算过程中的中间结果。因为在运算过程中，可能会出现溢出现象，用变形补码进行数据存储可以防止在运算过程中的溢出，从而尽量减少对最终结果的干扰（只要最终结果不溢出就可以了）。
| Decimal | 补码 | 变形补码 | Decimal | 取反 | 补码 | 变形补码 |
| 0 | 0000 | 0 0000 | -0 | 1111 | 0000 | 0 0000 |
| 1 | 0001 | 0 0001 | -1 | 1110 | 1111 | 1 1111 |
| ...... | ...... | ...... | ...... | ...... | ...... | ...... |
| 7 | 0111 | 0 0111 | -7 | 1000 | 1001 | 1 1001 |
| 8 | 1000 | 0 1000 | -8 | 0111 | 1000 | 1 1000 |
4's comlement 指双符号位，因为双符号位中 
= 4 ，同样的，我们前面介绍的补码则是 单符号位 2's comlement 。
在上面表格中我们可以看到， 8 的值太大，用 4 位补码无法表示，会出现溢出，但变形补码可以保留符号位和最高数值位。可以理解成在变形补码中，最高位为符号位，次高位可以用于表示数值。
要注意的是，+0 和 -0 的变形补码表示方式是一样的。
三、移码
移码的命名其实已经向我们解释了他的表示方法了。
移码表示是将每一个数加上一个偏置常数（Excess / bias），通常，当编码位数为 n 时，bias 取值为 
或者 -1 ( 例 IEEE 754 )。
其中，当bias 取 时，移码与补码仅第一位不同。
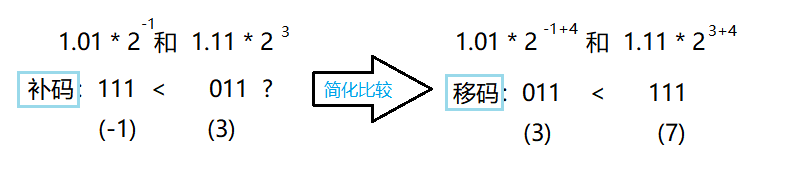
移码的作用：用移码表示浮点数的阶。
因为大多数计算机会采用科学计数法对浮点数进行存储，因此浮点数的大小比较一大部分是阶（指数）的比较，移码的加入会简化对指数的比较。例如：
