GraphSAGE论文阅读笔记
论文: Inductive Representation Learning on Large Graphs
1 Motivation
大多数graph embedding框架是transductive(直推式的), 只能对一个固定的图生成embedding。这种transductive的方法不能对图中没有的新节点生成embedding。相对的,GraphSAGE是一个inductive(归纳式)框架,能够高效地利用节点的属性信息对新节点生成embedding。
( 这里的transductive和inductive用的很精髓,统计机器学习可以分成两种: transductive learning, inductive learning.
transductive learning: To specific (test) cases, 指的是测试集是特定的(固定的样本);
inductive learning: 测试集不是特定的。
一般我们的目的是做 inductive learning。)
GNN中经典的DeepWalk, GCN方法都是transductive learning。
2 前向传播
论文中提出的方法称为graphSAGE, SAGE指的是 SAmple and aggreGat。 sample和aggregate就是主要的两步。
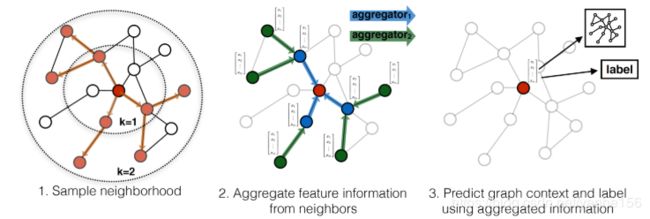
上面是为红色的目标节点生成embedding的过程。k表示距离目标节点的搜索深度,k=1就是目标节点的相邻节点,k=2表示目标节点相邻节点的相邻节点。
对于上图中的例子,
第一步是采样,k=1采样了3个节点,对k=2采用了5个节点;
第二步是聚合邻居节点的信息,获得目标节点的embedding;
第三步是使用聚合得到的信息,也就是目标节点的embedding,来预测图中想预测的信息;

伪代码中2到7行的两层循环,for k = 1 … K k=1 \ldots K k=1…K 表示深度从1到最大值K,for v ∈ V v \in \mathcal{V} v∈V 表示对图中的每个节点。
N ( v ) \mathcal{N}(v) N(v) 表示节点v的邻居,伪代码中也说明了 N \mathcal{N} N 表示neighborhood function。
第4行里, { h u k − 1 , ∀ u ∈ N ( v ) } \left\{\mathbf{h}_{u}^{k-1}, \forall u \in \mathcal{N}(v)\right\} {huk−1,∀u∈N(v)} 表示节点 v v v的任意相邻节点的聚合信息的集合, h N ( v ) k \mathbf{h}_{\mathcal{N}(v)}^{k} hN(v)k 是一个向量,表示从节点 v v v的相邻节点获取的信息。AGGREGATE k _{k} k 表示可微分的聚合函数,这篇文章后面尝试了多种方法。注意 k − 1 k-1 k−1不表示相邻,表示相邻的是 N ( v ) \mathcal{N}(v) N(v)。
第5行,将从相邻节点获取的信息 h N ( v ) k \mathbf{h}_{\mathcal{N}(v)}^{k} hN(v)k , 和这个节点自身的信息 h v k \mathbf{h}_{v}^k hvk拼接。
每个节点用特征来初始化得到一个初始表示 h v 0 h_v^0 hv0。当 k = 1 k=1 k=1时,跑完 for v ∈ V v \in \mathcal{V} v∈V 这个内层循环后,得到了 h v 1 h_v^1 hv1,每个节点的表征向量 h v 1 h_v^1 hv1包含了相邻节点的信息。 之后 k = 2 k=2 k=2, 跑完 for v ∈ V v \in \mathcal{V} v∈V 循环,从 h v 1 h_v^1 hv1得到了 h v 2 h_v^2 hv2, 但是注意, h v 1 h_v^1 hv1已经包含了相邻节点的信息,所以 h v 2 h_v^2 hv2包含了深度为2的相邻节点的信息。
同样的,每个节点的表征向量 h v k h_v^k hvk包含了深度为k的相邻节点的信息。
对图中的所有的节点 v ∈ V v \in\mathcal{V} v∈V循环K次,得到每个节点的表征向量就包含了相邻深度为K的节点信息,也就是我们最终想得到的节点的表示。
可以发现,对一个新加入的节点a,只需要知道其自身特征和相邻节点,就可以得到其向量表示。不必重新训练得到其他所有节点的向量表示。当然也可以选择重新训练。但是需要保存所有节点深度为k的表示,用于从 h a 0 h_a^0 ha0生成 h a 1 h_a^1 ha1, h a 2 h_a^2 ha2 … h a K h_a^K haK。
正如论文中所说的:
The intuition behind Algorithm 1 is that at each iteration, or search depth, nodes aggregate information
from their local neighbors, and as this process iterates, nodes incrementally gain more and more
information from further reaches of the graph.
这个算法直观的想法是,每次迭代,或者说每个深度,节点从相邻节点获得信息。随着迭代次数的增多,节点增量地从图中的更远处获得更多的信息。
节点采样 Neighborhood definition
graphSAGE并不是使用全部的相邻节点,而是做了固定尺寸的采样。
3 参数训练
论文给出的是无监督损失,希望相邻节点有相似的embedding,无关节点的embedding有明显差别。(类似word2vec,学习表征是无监督的,跟下游任务无关)
J G ( z u ) = − log ( σ ( z u ⊤ z v ) ) − Q ⋅ E v n ∼ P n ( v ) log ( σ ( − z u ⊤ z v n ) ) J_{\mathcal{G}}\left(\mathbf{z}_{u}\right)=-\log \left(\sigma\left(\mathbf{z}_{u}^{\top} \mathbf{z}_{v}\right)\right)-Q \cdot \mathbb{E}_{v_{n} \sim P_{n}(v)} \log \left(\sigma\left(-\mathbf{z}_{u}^{\top} \mathbf{z}_{v_{n}}\right)\right) JG(zu)=−log(σ(zu⊤zv))−Q⋅Evn∼Pn(v)log(σ(−zu⊤zvn))
z u , ∀ u ∈ V \mathbf{z}_{u}, \forall u \in \mathcal{V} zu,∀u∈V 表示图中任意节点的embedding。
v v v 表示在一个固定长度的随机游走上和节点 u u u一同出现过的节点
P n P_n Pn是负采样的分布
Q Q Q 表示负采样的数量
其实这个loss很常规,特殊的地方在于生成节点的表示 z u \mathbf{z}_u zu时,利用了相邻节点的特征。 也就是在于前向传播比较特殊。
这种无监督设置不考虑下游任务,类似于像下游任务提供节点的特征。
当节点的表示z只用于特定下游任务时,训练时无监督损失可以被替换成特定任务的损失,比如交叉熵。
4 Aggregator Architectures
这篇文章尝试了多种aggregator function。
(aggregator 的作用是把一个向量的集合转换成向量,,也就是聚合。)
和其他机器学习任务中的数据(如图像,文本等)不同,图中的节点是没有顺序的(node’s neighbors have no natural ordering)。aggregator function操作的是一个无序的向量集合 { h u k − 1 , ∀ u ∈ N ( v ) } \left\{\mathbf{h}_{u}^{k-1}, \forall u \in \mathcal{N}(v)\right\} {huk−1,∀u∈N(v)}。所以这个aggregator function需要symmetric, 或者说 invariant to permutations of its input。通俗来说就是输入顺序不影响函数结果。
所以aggregator function有两个性质:
- 可微 differentiable
- symmetric
Mean aggregator
显然对向量集合,对应元素取均值是最直接的想法。
这篇文章说取均值和图卷积是等价的,还推导出了一种GCN方法的变体。(我对GCN还不怎么熟,还不能想到怎么推广得)
用下面这个式子替换掉伪代码中的第4,5行
h v k ← σ ( W ⋅ MEAN ( { h v k − 1 } ∪ { h u k − 1 , ∀ u ∈ N ( v ) } ) \mathbf{h}_{v}^{k} \leftarrow \sigma\left(\mathbf{W} \cdot \operatorname{MEAN}\left(\left\{\mathbf{h}_{v}^{k-1}\right\} \cup\left\{\mathbf{h}_{u}^{k-1}, \forall u \in \mathcal{N}(v)\right\}\right)\right. hvk←σ(W⋅MEAN({hvk−1}∪{huk−1,∀u∈N(v)})
原始第4,5行是
h N ( v ) k ← \mathbf{h}_{\mathcal{N}(v)}^{k} \leftarrow hN(v)k← AGGREGATE k ( { h u k − 1 , ∀ u ∈ N ( v ) } ) _{k}\left(\left\{\mathbf{h}_{u}^{k-1}, \forall u \in \mathcal{N}(v)\right\}\right) k({huk−1,∀u∈N(v)})
h v k ← σ ( W k ⋅ CONCAT ( h v k − 1 , h N ( v ) k ) ) \mathbf{h}_{v}^{k} \leftarrow \sigma\left(\mathbf{W}^{k} \cdot \operatorname{CONCAT}\left(\mathbf{h}_{v}^{k-1}, \mathbf{h}_{\mathcal{N}(v)}^{k}\right)\right) hvk←σ(Wk⋅CONCAT(hvk−1,hN(v)k))
可以看到替换后,是对 h v k − 1 h_v^{k-1} hvk−1 和集合 { h u k − 1 , ∀ u ∈ N ( v ) } \left\{\mathbf{h}_{u}^{k-1}, \forall u \in \mathcal{N}(v)\right\} {huk−1,∀u∈N(v)}取并集,然后一起算均值,再乘上权重。
LSTM aggregator
和mean aggregator相比,LSTM有更大的表达能力。但是LSTM不符合symmetric的性质,输入是有顺序的。所以把相邻节点的向量集合随机打乱顺序,然后作为LSTM的输入。
Pooling aggregator
尝试了pooling做aggregator, 所有相邻节点的向量共享权重,先经过一个非线性全连接层,然后做max-pooling.
AGGREGATE k pool = max ( { σ ( W pool h u i k + b ) , ∀ u i ∈ N ( v ) } ) _{k}^{\text { pool }}=\max \left(\left\{\sigma\left(\mathbf{W}_{\text { pool }} \mathbf{h}_{u_{i}}^{k}+\mathbf{b}\right), \forall u_{i} \in \mathcal{N}(v)\right\}\right) k pool =max({σ(W pool huik+b),∀ui∈N(v)})
5 实验结果
实验给了三个图,效果,效率,采样数量对效果和性能的影响。
三个数据集上的实验结果表明,一般是LSTM或pooling效果比较好。有监督都比无监督好。
相比于只用特征的逻辑回归,效果都是有提升的。
(但是不知道和LightGBM相比效果怎么样)
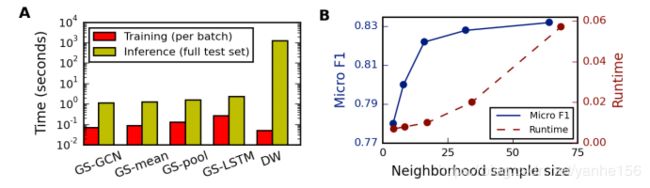
在79534个测试集上的推理时间是秒级的。(感觉上还行,也不是特别快)
右图显示随着采样数量增大,运行时间接近线性增大。但是效果并不是线性变好。
代码
作者在论文里用的tensorflow,但是也开源了一个简单, 容易扩展的pytorch版本。
pytorch版本中用的两个数据集都比较小,不是论文里用的数据集。这两个数据集在Kipf 16年经典的GCN论文用到了。节点数量分别约是2700,20000。
cora是一个机器学习论文引用数据集,提供了2708篇论文的引用关系,每篇论文的label是论文所属的领域。
label一共七种,包括遗传算法,神经网络,强化学习等7个领域。
特征是已经经过stemming和stopwords处理过的词表,每列表示一个词是否出现。