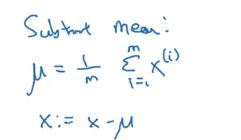吴恩达深度学习——深度学习的实用指南
文章目录
- 引言
- 构建数据
- 偏差与方差
- 训练神经网络的基本方法
- 正则化
- 为什么正则化可以减少过拟合
- Dropout正则化
- 为什么Dropout会生效
- 其他正则化方法
- 提前停止
- 归一化输入
- 梯度消失与梯度爆炸
- 神经网络的权重初始化
- 梯度的数值逼近
- 梯度检验
- 关于梯度检测实现的注意事项
- 参考
引言
本文是吴恩达深度学习第二课:改善深层网络的笔记。这次内容包括深度学习的实用技巧、提高算法运行效率、超参数调优。
第二课有以下三个部分,本文是第一部分。
- 深度学习的实用技巧
- 提高算法运行效率
- 超参数调优
构建数据
在训练神经网络时,我们要做许多决策:
- 网络的层数
- 隐藏层的单元数
- 学习率的取值
- 激活函数的选择
- …
我们不可能一开始就知道合适的结果,实际上应用深度学习是一个典型的迭代过程。
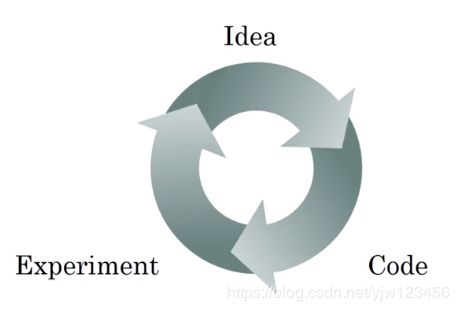
一开始可能有一个初步想法,比如我们要构建一个特定层数的神经网络、隐藏单元的数量。然后编码尝试运行这些代码,接着测试这些选择运行的结果,然后可能需要根据结果来完善我们的想法、改变最初的选择。
我们可能需要循环上面这个迭代很多次才能得到比较满意的效果,因此算法训练速度的一个关键因素就是循环效率。
通常将整个数据集分成三份——训练集、验证集合测试集。而创建高质量的训练(数据)集、验证(数据)集和测试集能提高循环效率。
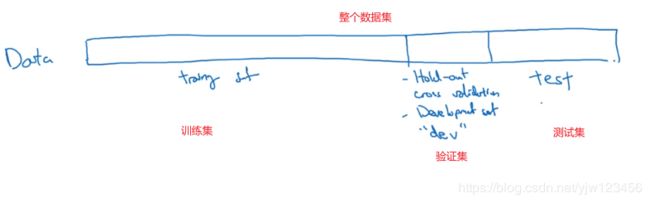
一开始我们对训练集执行训练算法,然后通过验证集(交叉验证)选择最好的模型,最后在测试集上进行评估。
在机器学习发展的小数据量时代(1万个样本左右),通常将数据按照70%/30%的比例划分(训练集和测试集,该情况下无验证集),或者是60%/20%/20%的比例来划分。
但在当今大数据时代,我们可能有百万级别的数据量。此时验证集和测试集占数据总数的比例会越来越小。因为验证集的目的就是验证不同的算法,如果有100万条数据,那么取1万条做为验证集足矣。
同样测试集的目的就是正确评估分类器的性能,如果有100万条数据,我们只需要1万条数据亦可。
因此此时的比例是98%/1%1%
现在深度学习另一个趋势是在训练和测试集分布不匹配的情况下进行训练。
由于深度学习需要大量的数据来做训练,为了获得大量数据,我们通过会通过爬虫来抓取网上的数据,代价就是训练集与验证/测试集数据分布不同。
假设我们构建好了猫分类器,然后发布到线上,用户可以上传自己的图片来识别其中是否含有猫。

可能训练数据是从网上下载的图片,验证/测试数据是用户上传的图片。结果网页上的猫图片分辨率很高(拍照技术很专业、后期制作精良),而用户上传的照片可能是用手机随意拍摄的。
所以训练集和验证/测试集可能不同,这种情况下建议确保验证集和测试集的数据来自同一分布。
因为我们需要用验证集来评估不同的模型、优化模型的性能,如果验证集和测试集来自同一分布那么就很OK。
所以说搭建训练、验证与测试集能加速神经网络的集成,也可以更有效地衡量算法的偏差和方差,从而有助于我们选择合适的方法来优化算法。
偏差与方差
什么是偏差(bias)与方差(variance)呢,我们看个例子。
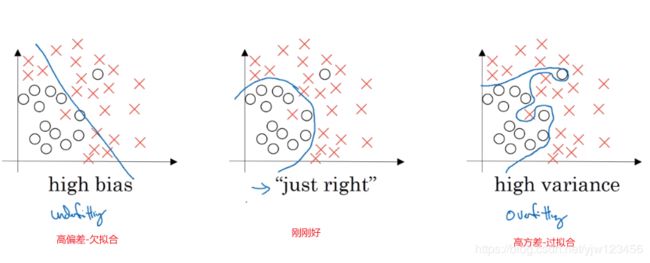
假设我们有份上图这样的数据分布,上面是三种划分结果,分别对应于高偏差、刚好以及高方差。
上面的数据只有两个特征,还可以可视化。如果有多个特征(超3个),那么就无法可视化了。
所以我们要通过一些指标来研究偏差和方差。
理解偏差和方差的两个关键指标是训练集错误率和验证集错误率。
我们以猫分类算法为例。

假设有个算法训练集错误率是1%,而验证集错误率是11%。可以看到训练集分类效果好,而验证集就较差,我们可能过拟合了训练集。这种情况就是高方差。

第二种情况是训练错误为15%,验证集错误率为16%,我们说这个算法对训练数据的拟合度不够,是欠拟合的,此时就是高偏差。但是这种情况下验证集错误率较正常,只比训练集高了一点。

如果训练错误率15%,验证错误率30%,这种情况就是高偏差同时高方差。

如果训练错误率0.5%,验证错误率1%,这种情况非常理想,为低偏差同时低方差。
上面的这些分析都是基于假设人类的预测错误率为0%,同时训练集和验证集同分布,这种最优误差也被称为基本误差。
如果最优误差也很高,比如15%的话,那么下面这种情况就是很合适的。

训练神经网络的基本方法
当我们训练好基本模型后,我们首先要知道算法的偏差高不高(在训练集上评估)。如果偏差较高,我们需要选择一个更加复杂的网络,可能有更多的隐藏层或隐藏单元,或者增大迭代次数,或尝试更好的优化算法。 不断尝试上面的方法,直到解决了高偏差问题。
一旦高偏差的问题解决了,就要看算法的方差高不高(在验证集上评估)。如果方差较高,那么我们可以尝试获得更多的数据,或者通过正则化来减少过拟合,有时需要尝试更合适的神经网络架构。
总之要不断尝试,直到找到一个低偏差、低方差的神经网络。
在小数据量时代经常听到要平衡偏差和方差,但在当前的深度学习和大数据时代,只要持续训练一个更大的网络(适当正则化),并且准备了更多数据,我们有工具可以在减少偏差或方差的同时不对另一方产生过多不良影响。
上面提到了正则化是什么呢,下面我们就来看一下。
正则化
如果你怀疑神经网络过拟合了数据,即存在高方差问题,那么最先想到的方法应该是正则化。
另一种可靠的方法是准备更多的数据(但实际这种方法可能不可行)。
我们先看下逻辑回归的正则化。
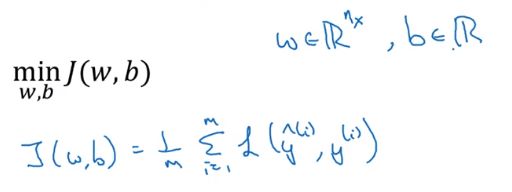
在逻辑回归中我们想要最小化成本函数,如果加入正则化只要在上面的式子后面加上一个后缀即可,如下:
这里为什么只用了参数 w w w,没有加上参数 b b b呢。因为 w w w通常是一个高维度向量,已经可以表达高偏差问题,而 b b b只是一个标量。实际上如果加上 b b b也不会有什么影响。
L2正则化是常用的正则化方法,那么有没有L1正则化呢,有的

其实这里的L1和L2指的就是范数,以下摘自人工智能数学基础之线性代数。

如果使用L1正则化,那么 w w w会很稀疏,也就是 w w w向量中有很多0。
还有一个细节要说的是, λ \lambda λ正则化参数是一个超参数, λ \lambda λ过小容易导致过拟合,而多大容易导致欠拟合。我们通常使用验证集或交叉验证来配置这个参数,以平衡过拟合与欠拟合。
在python中我们用lamda来代表 λ \lambda λ。
上面就是逻辑回归中实现L2正则化的过程,那神经网络呢
上面这个矩阵范数被称为 弗罗贝尼乌斯范数 (Frobenius norm),下标为 F F F。(其实可以想成是L2范数)
现在如何用该范数实现梯度下降呢?

只要对上面的正则项求对 W [ l ] W^{[l]} W[l]的偏导即可,只考虑 l l l层,其他层的参数当初常数,也就是其他层参数偏导为零。

如果只看这一项的话

相当于 W [ l ] W^{[l]} W[l]乘以了 ( 1 − α λ m ) (1 - \frac{\alpha \lambda}{m}) (1−mαλ),这个式子是小于1的,也就是权重越来越小。
这就是为什么L2范数也被称为权重衰减,知道就行了。
上面就是神经网络中应用L2正则的过程,但是为什么正则化能减少过拟合呢。且看下节分析。
为什么正则化可以减少过拟合
为什么正则化可以减少过拟合,来看两个例子。
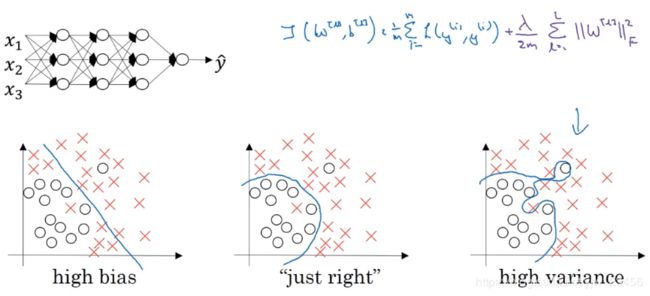
假设这是一个过拟合的神经网络,现在我们加上了紫色的正则化项来减少过拟合,为什么加上这项可以减少过拟合呢,直观上理解就是如果 λ \lambda λ足够大,就会导致损失值很大,为了减少损失值,权重矩阵 W W W会趋近于零。
也就是把很多神经元的权重设为零,这样会消除了这些隐藏神经元的影响,相当于简化了这个神经网络,得到一个由权重非零的神经元组成的很小的网络。可能小到如同一个逻辑回归单元,但是深度很大。这会使过拟合状态更接近于高偏差的状态。
但是 λ \lambda λ会存在一个中间值,使得结果接近于中间刚刚好(just right)的状态。
这只是直观上的理解,其实该神经网络的所有隐藏单元依然存在,只不过影响变小了,使得复杂的神经网络变简单了。
下面再来看一个例子,假设使用tanh激活函数,

如果 ∣ z ∣ |z| ∣z∣值很大,那么该函数越接近于非线性部分,因此我们增加 λ \lambda λ来减少 W W W,使得 z [ l ] z^{[l]} z[l]更接近于线性部分(上图红线标出的那部分),那么每层几乎都是线性的。那么整个网络就是一个线性网络,哪怕有很深的层数。 我们知道线性函数不适合做非常复杂的决策,它的决策便边界是一条直线。
这样就不容易过拟合训练数据。
这就是为什么L2正则化能减少过拟合。在深度学习中还有一种方法也用到了正则化,就是dropout(抓爆?)正则化。
Dropout正则化
还有一个非常实用的正则化方法——Dropout(随机失活)

假设上面这个NN存在过拟合,应用Dropout正则化的思路是这样的,dropout会遍历网络的每一层,同时设置消除NN中节点的概率。
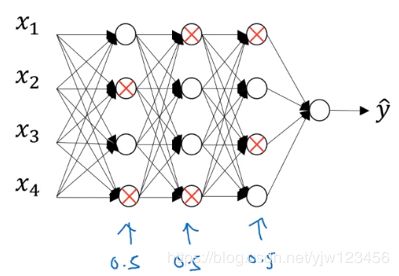
假设以抛硬币的方式设置概率,每层的消除概率是0.5,大概每层都会消除两个节点,然后就可以删掉这些节点进出的连线。

这样就可以得到一个更简单,节点更少的NN。然后可以使用反向传播方法来进行训练,对于不同的样本,也会以抛硬币的方式设置概率,保留一类节点集合,同时删除其他节点集合。
这样对每个训练样本,都会以这种方式生成精简的神经网路来训练它。
那如何实现dropout呢,下面以一个三层的网络来说明。
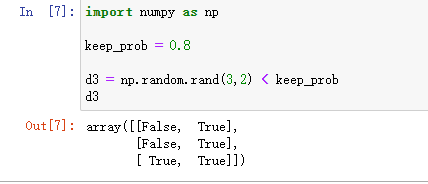
首先定义 d 3 d^3 d3,d3 = np.random.rand(a3.shape[0],a3.shape[1]) < keep_prob,这个keep_prob是保留概率(保留概率 = 1 - 消除概率),上面的例子中保留概率是0.5。这个例子中设成0.8,意味着消除任一隐藏单元的概率是0.2。 所以上面代码的作用是生成随机矩阵。
d3会是一个矩阵,每个样本和每个隐藏单元,它们在d3中对应值为1(True)的概率都是0.8。
接下来要从第三层中获取激活值a3 = np.multiply(a3,d3),它的作用是过来掉d3中所有等于0的元素。

最后我们要扩展a3 = a3 / keep_prob,为什么要这么做。假设第三层隐藏层上有50个单元,如果保留概率为0.8,意味着平均有50 * 0.2 = 10个单元被删除(归零)。
我们来看下 Z [ 4 ] = W [ 4 ] ⋅ a [ 3 ] + b [ 4 ] Z^{[4]} = W^{[4]} \cdot a^{[3]} + b^{[4]} Z[4]=W[4]⋅a[3]+b[4],现在 a [ 3 ] a^{[3]} a[3]中有20%的单元被归零。
为了不影响 Z [ 4 ] Z^{[4]} Z[4]的值,我们需要用 a [ 3 ] / = 0.8 a^{[3]} /= 0.8 a[3]/=0.8,这样会修正我们需要的那20%。(上面40 / 0.8 = 50),那么a3的期望值就不会变。
a 3 / = 保 留 率 \boxed{a3 /= 保留率} a3/=保留率 就是所谓的 inverted dropout(反向随机失活) 方法,它可以确保a3的期望值不变。
现在我们用的是 d 3 d^3 d3向量,我们会发现对于不同的训练样本来说,通常被清除的隐藏单元也不同。实际上,如果通过相同训练集多次传递数据,每次训练数据的梯度不同,那么应该随机对不同的隐藏单元归零。
向量 d 3 d^3 d3决定第三层中哪些单元归零。
那在测试时如何预测呢,在测试阶段一般不使用dropout函数,因为在测试时,我们期望输出结果不是随机的。
后面会通过编程来加深对dropout的理解。
为什么Dropout会生效
Dropout可以随机删除神经网络中的神经元,这看起来有点疯狂,为什么还可以发挥作用呢。
在上小节中我们对Dropout有了一个直观的理解,就是变成了一个更小、更简单的神经网络,就可以减少过拟合。
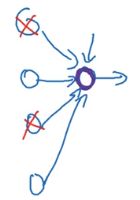
用了Dropout后,有些神经元会被消除。这样上面这个紫色的神经元不能依赖任何特征,因为任何特征都可能被随机消除。 这样就不能给某个特征特别大的权重,因为它可能被消除。
因此只会给这4个输入特征一点权重,然后通过传播所有权重,Dropout将产生收缩权重的平方范数的效果(类似L2正则化)。
在应用Dropout时,我们要设置的一个参数是keep_prob,不同层的这个保留率也可以不同。
参数较多的层可以把keep_prob设的比较小,参数较少的层设的大。如果在某一层不用担心过拟合问题,还以直接设成1(意味着保留所有神经元)。
Dropout的一大缺点是代价函数不再被明确定义,所以通常的做法是先不开启Dropout,运行代码,确保代价函数单调递减,然后如果发生了过拟合,再打开Dropout。
下面我们一起看下其他正则化方法。
其他正则化方法
假设我们在拟合猫图片分类器,如果想通过扩大训练数据集来解决过拟合问题,但是通常很难扩展数据集。
但是我们可以对图片进行一些处理来扩展数据集,比如水平翻转图片后将它假如到训练集。这样训练集的数据量可以增大一倍。

除了水平翻转图片,还可以随意裁剪图片。

和全新的猫图片数据相比,这些假数据虽然没有那么多信息,但是这样做几乎没有任何代价。

对于数字识别等问题还可以通过随意选择或扭曲数字来扩充数据。
提前停止
还有一种常用的方法叫early stopping。
在运行梯度下降时我们可以画出训练误差和验证集误差。
通常会发现验证集误差先是呈下降趋势,然后在某个时间点后开始上升。
而early stopping的思想是我们可以在红点处停止训练,因为过了该点后验证集误差就要增大了。
通常会在红点处得到一个 W W W值中等的 ∣ ∣ w ∣ ∣ F ||w||_F ∣∣w∣∣F。
有时我们会使用early stopping,但是它也有一个缺点。
就是不能同时处理最小化代价函数和正则化的问题。因为提前停止了训练就会停止优化代价函数,这样代价函数值不会很小,同时又希望不出现过拟合。此时没有采用不同的方式来解决这两个问题。这样可能考虑的东西会变成更复杂。
如果不用early stopping的话,则可以使用L2 正则化,这样我们可以尽可能的训练神经网络久一点,因为要尝试不同的 λ \lambda λ参数值(缺点)。
early stopping的有点就是只需要运行一次梯度下降就可以找到 W W W的较小值,中间值,和较大值。
归一化输入
在训练神经网络时,一个加速训练的方法就是归一化输入。

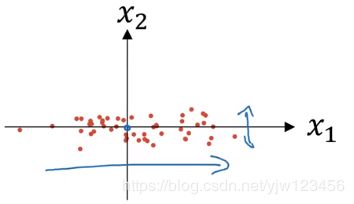
假设我们有一个训练集,它有两个输入特征,上面是训练集的散点图。
归一化输入需要两个步骤,第一步是均值归零:让每个样本值减去均值即可。
第二个步骤是方差归一化,我们这里 x 1 x_1 x1的方差要比 x 2 x_2 x2大得多。
σ 2 = 1 m ∑ i = 1 m ( x ( i ) ) 2 x / = σ 2 \sigma^2 = \frac{1}{m} \sum_{i=1}^m (x^{(i)})^2 \\ x /= \sigma^2 σ2=m1i=1∑m(x(i))2x/=σ2

经过方差归一化后,训练集的分布就成了下面这样:

这样 x 1 , x 2 x_1,x_2 x1,x2的方差都等于1,均值都为0。
如果用它来调整训练数据,那么需要用同样的(训练集上的) μ , σ 2 \mu, \sigma^2 μ,σ2来调整测试数据。
那么为什么要归一化输入数据呢

如果不归一化输入并且 x 1 , x 2 x_1,x_2 x1,x2的取值返回相差很大,比如 x 1 x_1 x1取值从1到1000,而 x 2 x_2 x2取值在0到1。
那么代价函数可能会像上面这样一个狭长的碗。上面是一个三维图像,如果用二维图像的话就是:
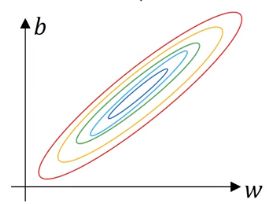
如果归一化输入后,代价函数看起来就会更加对称。
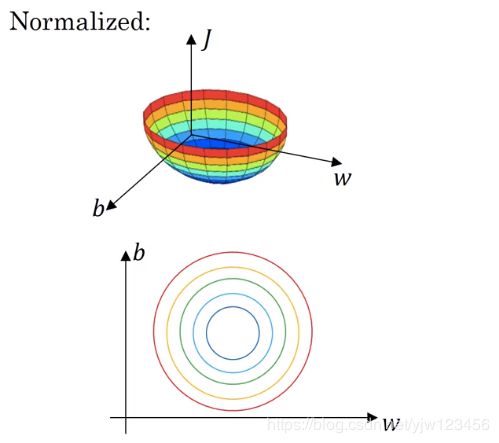
如果在未归一化的数据上进行训练,梯度下降法可能需要多次迭代过程,像下面这样:

而使用归一化后,梯度下降法能更快的找到最小值。

如果数据范围相差不大,那么就不需要归一化,但是做了归一化也没有什么害处。
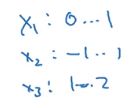
梯度消失与梯度爆炸
在训练深度神经网络还会面临的一个问题是梯度消失或梯度爆炸。因为在训练深度网络时,梯度有时变得非常大或非常小。

假设要训练这样一个深度网络,为了简单起见,让激活函数 g = z , b [ l ] = 0 g = z, b ^{[l]} = 0 g=z,b[l]=0。
就是一个线性激活函数,并且忽略了偏差 b b b。
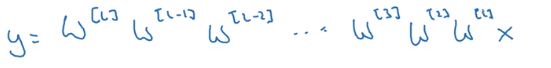
也就是输出会变成 y ^ = W [ L ] W [ L − 1 ] W [ L − 2 ] ⋯ W [ 3 ] W [ 2 ] W [ 1 ] x \hat y = W^{[L]} W^{[L-1]} W^{[L-2]} \cdots W^{[3]} W^{[2]} W^{[1]} x y^=W[L]W[L−1]W[L−2]⋯W[3]W[2]W[1]x

然后我们可以计算出 z [ 1 ] = w [ 1 ] x z^{[1]}=w^{[1]}x z[1]=w[1]x和 a [ 1 ] = g ( z [ 1 ] ) = z [ 1 ] a^{[1]}=g(z^{[1]}) = z^{[1]} a[1]=g(z[1])=z[1]。
接着 a [ 2 ] = g ( z [ 2 ] ) = g ( w [ 2 ] a [ 1 ] ) a^{[2]} = g(z^{[2]}) = g(w^{[2]} a^{[1]}) a[2]=g(z[2])=g(w[2]a[1]),然后是 a [ 3 ] , a [ 4 ] , ⋯ a^{[3]} ,a^{[4]}, \cdots a[3],a[4],⋯
假设隐藏层每层的权重 W [ l ] W^{[l]} W[l]的值是这样的:

那么 y ^ \hat y y^就等于 W [ L ] ( W [ l ] ) ( L − 1 ) x W^{[L]} (W^{[l]} )^{(L-1)} x W[L](W[l])(L−1)x
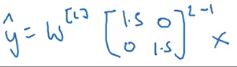
这里是 W [ l ] W^{[l]} W[l]的 ( L − 1 ) (L-1) (L−1)次。相当于 y ^ = 1. 5 ( L − 1 ) x \hat y = 1.5^{(L-1)} x y^=1.5(L−1)x,如果 L L L很大的话,那么输出值就会很大。
相反地,如果权重是0.5

那么 y ^ \hat y y^相当于是 0. 5 ( L − 1 ) x 0.5^{(L-1)} x 0.5(L−1)x,也就是使得输出值变得非常小。
也就是说,只要 W [ l ] W^{[l]} W[l]的值比 1 1 1大一点,那么神经网络的激活值就会爆炸式增长;只要 W [ l ] W^{[l]} W[l]的值比 1 1 1小一点,那么神经网络的激活值会以指数级递减。
这样会导致训练难度上升,并且因为梯度会变得非常小,导致训练时间也会变长。
神经网络的权重初始化
针对上小节梯度消失和梯度爆炸的问题,有一个有用的解决方法是,谨慎的选择随机初始化参数。
先看一个神经元的例子

同样这里忽略 b b b,为了防止 z z z过大或过小,可以看到,当 n n n越大,我们希望 W i W_i Wi越小。
一种合理的做法是设置 W i W_i Wi 为 1 n \frac{1}{n} n1的某种关系。 n n n是上面输入特征的数量。

这里在初始化 W [ l ] W^{[l]} W[l]时让随机值乘以上一层的单元数 n [ l − 1 ] n^{[l-1]} n[l−1]开根号的倒数,即 1 n [ l − 1 ] \sqrt \frac{1}{n^{[l-1]}} n[l−1]1,这种方法就是Xavier 初始化。
这种方法适用于tanh激活函数,如果是Relu激活函数,后面乘以的就是 2 n [ l − 1 ] \sqrt \frac{2}{n^{[l-1]}} n[l−1]2。
这些方法针对输入特征的规模给定不同范围的权重初始值。
梯度的数值逼近
在实现反向传播时,有一个测试叫梯度检验,它的作用是确保反向传播正确实施。
为了逐渐实现梯度检验,我们先看下如何对梯度做数值逼近。
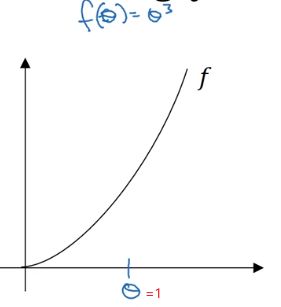
假设激活函数 f ( θ ) = θ 3 f(\theta) = \theta^3 f(θ)=θ3 ,导数 g ( θ ) = 3 θ 2 g(\theta) = 3 \theta^2 g(θ)=3θ2
先看下 θ = 1 \theta = 1 θ=1的位置,我们再 θ \theta θ的右侧设置一个 θ + ϵ \theta + \epsilon θ+ϵ,在左侧设置一个 θ − ϵ \theta - \epsilon θ−ϵ。 ϵ \epsilon ϵ通常是一个很小的值,比如 0.01 0.01 0.01。

然后看下上面绿色的三角形,计算高和宽的比值,就是梯度的估计,

然后用宽度为 2 ϵ 2 \epsilon 2ϵ的三角形(较大的三角形)高宽比值作为逼近 θ \theta θ的导数。
下面写一下公式,
f ( θ + ϵ ) − f ( θ − ϵ ) 2 ϵ ≈ g ( θ ) \frac{f(\theta + \epsilon) - f(\theta - \epsilon)}{2 \epsilon} \approx g(\theta) 2ϵf(θ+ϵ)−f(θ−ϵ)≈g(θ)
我们来计算验证一下,当 θ = 1 , ϵ = 0.01 \theta =1,\epsilon=0.01 θ=1,ϵ=0.01
( 1.01 ) 3 − ( 0.99 ) 3 0.02 = 3.0001 \frac{(1.01)^3 - (0.99)^3}{0.02} = 3.0001 0.02(1.01)3−(0.99)3=3.0001
g ( θ ) = 3 θ 2 = 3 g(\theta) = 3 \theta^2 = 3 g(θ)=3θ2=3
所以这两个结果很逼近,误差是 0.001 0.001 0.001。
梯度检验
梯度检验可以帮我发现反向传播过程中的bug。我们这小节来看下如果用它来检验反向传播实施是否正确。
为了执行梯度检验,首先需要把所有的参数转换成一个巨大的向量数据。
![]()

那么代价函数就可以写成 J ( θ ) J(\theta) J(θ),
![]()
接着把对应的梯度也放到一个大向量中。
现在的问题是 J J J的梯度与 d θ d\theta dθ有什么关系。
为了实现梯度检测,我们需要下面的循环:
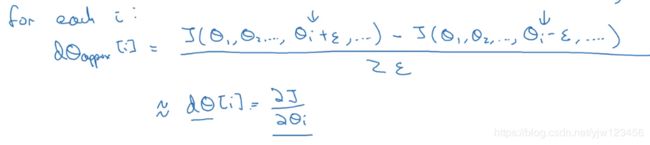
代入上小节的公式,用 d θ a p p r o x [ i ] d\theta_{approx}[i] dθapprox[i]来逼近 d θ [ i ] d\theta[i] dθ[i] i i i来遍历所有的参数。
现在要做的就是检测它们两个是否接近,可以计算
∣ ∣ d θ a p p r o x − d θ ∣ ∣ 2 ∣ ∣ d θ a p p r o x ∣ ∣ 2 + ∣ ∣ d θ ∣ ∣ 2 \frac{||d\theta_{approx} - d\theta||_2}{||d\theta_{approx}||_2 + ||d\theta||_2} ∣∣dθapprox∣∣2+∣∣dθ∣∣2∣∣dθapprox−dθ∣∣2
这个比值是否为一个很小的值,比如 1 0 − 7 10^{-7} 10−7,那么说明导数逼近是正确的,即我们反向传播的代码是没问题的。
如果比值为 1 0 − 5 ) 10^{-5}) 10−5),那么要小心了,可能需要检查一下我们的代码。
如果比值大于 1 0 − 3 ) 10^{-3}) 10−3),那么可能我们的代码就有bug了。
关于梯度检测实现的注意事项
- 不要在训练时使用梯度检测,只用于调试(因为计算 d θ a p p r o x d\theta_{approx} dθapprox会很耗时)
- 如果算法的梯度检测失败,那么要检查每一项,试着找出bug(如果 d θ a p p r o x [ i ] d\theta_{approx}[i] dθapprox[i]与 d θ d\theta dθ的值相差很大,那么要查找不同的 i i i值来发现是哪个导致这个差值很大)
- 如果使用了正则化,那么别忘了正则化项的梯度
- 不要与dropout一起使用
- 在随机初始化过程中运行梯度检测,然后再训练网络,反复训练网络后,再重新运行梯度检测(这种情况不常见)
参考
1. 吴恩达深度学习
2. 吴恩达深度学习 专项课程(也可以去官网免费旁边,不能做练习题)
这门课程的核心是练习题,可以从练习题中学到很多,因此建议购买该课程解锁练习题。本人已经够了,花费了300多人民币,但这只是一个月的,因此争取在一个月学完。