多径衰落详解（整理）（一）

时变、多径是无线信道的特点，相信很多人在看了很多书之后，对无线信道感觉还是一头雾水。为什么多径导致频率选择性？为什么多普勒频移反映了信道的时变性？对这些问题感觉困惑的肯定大有人在。下面我们就用一个简单的不能再简单的程序一一解开你的困惑。

首先，我们先说一下程序模拟的场景。如图1所示。

                图.1 最简单的多径信道

假设在一条笔直的高速公路上一端安装了一个固定的基站，在另一端有一面完全反射电磁波的墙面，基站距离反射墙的距离为d。移动台距离基站初始距离为r0。基站发射一个频率为f的正弦信号，表示为cos(2*pi*f*t)。由于墙面的反射，移动台可以接收到2径信号，其中之一是从基站直接发射的信号，另一径是从反射墙反射过来的信号。

OK，首先我们来看移动台静止的情况。显然，从基站发出的直射信号到达移动台需要的时间为r0/c（c为光速），从反射墙反射过来的信号到达移动台所需要的时间为(d+d-r0)/c=(2d-r0)/c。换句话说，在时刻t，移动台分别接收到了从时刻(t-r0/c)基站发出的直射信号和从时刻t-(2d-r0)/c基站发出的反射信号。我们知道，信号在传播的过程中要衰减，自由空间中，电磁波功率随距离r按平方规律衰减，相应的电场强度(可以看成接收信号电压)随1/r规律衰减。并且反射信号同直射信号的相位相反。所以，时刻t移动台接收到的合成信号为

减号体现了反射信号与直射信号的相位相反。

在r0处的接收信号会有什么特点？让我们把它画出来。下面是程序代码。

clear all

f=1;        %发射信号频率

v=0;        %移动台速度，静止情况为0

c=3e8;     %电磁波速度，光速

r0=3;      %移动台距离基站初始距离

d=10;      %基站距离反射墙的距离

t1=0.1:0.0001:10;   %时间

E1=cos(2*pi*f*((1-v/c).*t1-r0/c))./(r0+v.*t1);

E2=cos(2*pi*f*((1+v/c)*t1+(r0-2*d)/c))./(2*d-r0-v*t1);

figure

plot(t1,E1)     %画出直射径的信号

hold on

plot(t1,-E2,'-g')      %画出反射径的信号

hold on

plot(t1,E1-E2,'-r')          %画出移动台总的接收信号。

legend('直射径信号','反射径信号','移动台接收的合成信号')

axis([0 10 -0.8 0.8])

运行程序后，结果如图2所示：

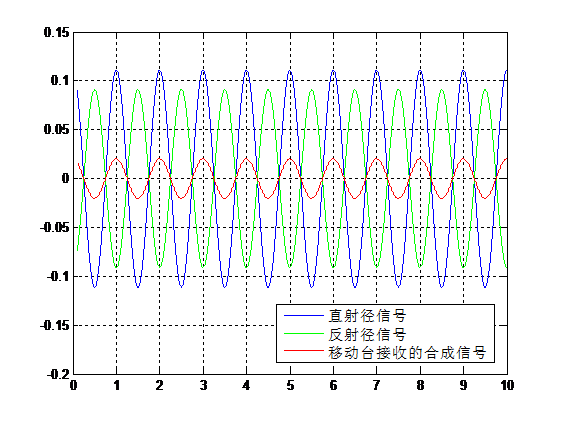
图2  r0=3时的直射信号、反射信号与合成信号

其中，蓝色线是直射径的信号，绿色线是反射径的信号，红色线则是移动台接收到的第1径和第2径的合成信号，从图中我们清楚的可以看出，即使移动台是静止的，由于反射径的存在，使得接收到的合成信号最大值要小于直射径的信号。

    下面我们改一下移动台距离基站的位置，让r0=9，使它更靠近反射墙的位置，再次运行程序，结果如图3所示：

 

图3  r0=9时的直射信号、反射信号与合成信号

    我们就可以得出这样的结论，即使移动台静止，由于反射径的存在，使接收信号要比没有反射径时的信号弱，衰落由此产生。

    且慢，我们在实验中只是发射了单1频率的信号，发射其它频率的信号结果会怎样呢？

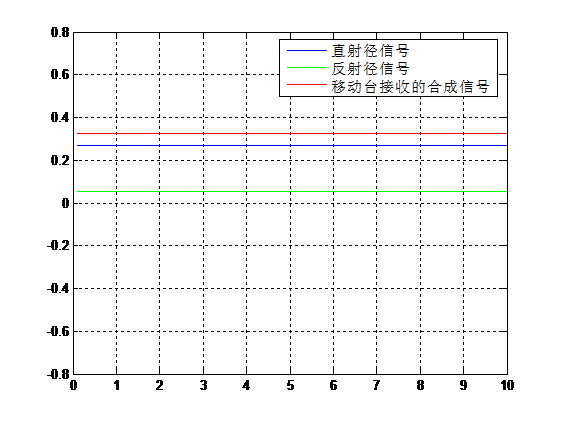
    我们把修改f=100e6，并且r0=3，结果如图4所示。这时候，由于f太大，因此所有的点都连成了一条直线。但是我们可以看到红线明显的大于蓝色线和绿色线，这说明在f=100e6时，移动台接收到的信号是得到了增强。

图4  f=100e6时的直射信号、反射信号与合成信号

    为了更直观的说明，我们把光速c改一下，让c=10，这样改动并不会影响讨论问题的实质，但可以帮助我们更直观的观察。分别让f=1和f=5，画出的图形分别如图5、图6所示：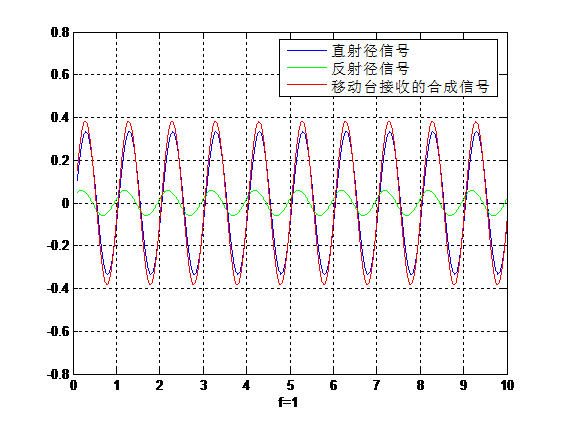

图5   f=1，c=10时的直射信号、反射信号与合成信号

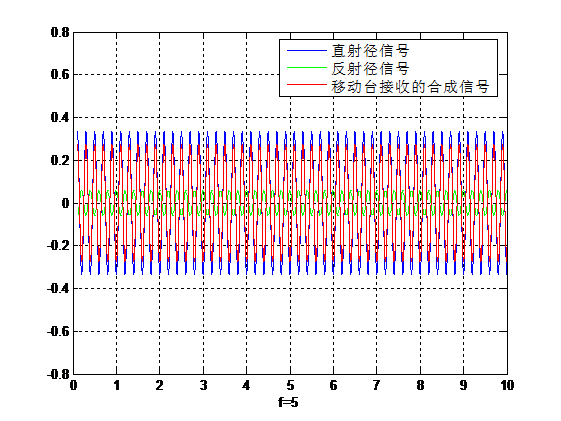
图6  f=5、c=10时的直射信号、反射信号与合成信号

从结果我们明显可以看出，这次是f=1的信号得到增强，而f=5的信号得到削弱。

我想，到这里，你应该明白频率选择性衰落是怎么回事了。在同一位置，由于反射径信号的存在，发射不同频率的信号时，在接收机处接收到信号有的频率是被增强了，有的频率是被削弱了。频率选择性由此产生。

既然有频率选择性衰落，我们自然会问，哪些频率会被增强，哪些频率会被削弱呢？

在上面的例子中，如果我们让c=3e8，让f=1，2，3…100,…,1000,你会发现这些频率基本上都是被削弱的，只有让f充分大，比如f=100e6，才会看出信号被增强了，那么我们就把那些受到的影响基本一致的频率范围叫做相干带宽。相干带宽如何得到呢？

从我们的实验中可以看出，接收信号是2个频率均为f的电波的叠加，这2个电波的相位差为：

从这个公式中，我们可以看出，对于固定的r，如果f改变则合成信号从波峰到达波谷，而  恰好是反射径与直射径的传播时延之差。如果频率的改变量远小于1/Td，则信号是增强还是削弱并不会出现明显的改变。一次参数1/Td就成为相干带宽。

有了相干带宽的概念，我们再来看平坦衰落与频率选择性衰落。

假设发射的信号带宽较窄，小于相干带宽，我们可以知道，信号的频带内受到的衰落影响基本是一致的。这时称这样的衰落为平坦衰落。学过信号系统的都知道，频带较窄，意味着时域的信号脉冲周期较长，当信号带宽恰好等于相干带宽时，可以近似的认为信号脉冲周期近似等于传播时延之差。此时，当移动台恰好接收到直射径的第2个脉冲时，从反射径到达的第1个脉冲也同时到达，因此合成信号就是直射径的第2个脉冲和反射径的第1个脉冲。看到这里，我们会明白码间干扰是如何产生的了。如果我们增大信号脉冲周期，相应的信号频带变窄，这时码间干扰会变小。也就说反射径第1个脉冲到达时，直射径的第1个脉冲还没有结束。脉冲周期越长，则直射径和反射径的脉冲重合的部分越多，码间干扰就越轻。当脉冲周期远大于时延差时，我们完全可以近似的把直射径的信号与反射径的信号看作是同一径信号。当然，信号的脉冲幅度会发生变化。当我们把更多反射径的信号基本看作同一径信号时，瑞利衰落由此产生。在存在更多反射径的情况下，各个径到达的方向不一样，相位不一样，可以看作服从同一分布的随机变量。由概率论的知识，多个服从同一分布随机变量的和服从高斯分布。由于实际的信号一般是通过I、Q两路传输，因此I路服从高斯分布，Q路服从高斯分布，包络则服从瑞利分布。看看瑞利分布的定义是不是也是这么来的？

上面是讨论了信号脉冲周期大于传播时延的情况，下面再讨论信号脉冲周期小于传播时延的情况。根据时频关系我们可以知道，脉冲周期短，意味着信号频带变宽，大于相干带宽。上面已经说过大于相干带宽后，频率受到的影响是不一样的。所以这时的衰落就是频率选择性衰落。再考虑时域的情况，脉冲周期变短。假设变为1/2传播时延差，当移动台接收到直射径的第3个脉冲时，反射径的第1个脉冲才到达。很明显，反射径的第1个脉冲对直射径的第3个脉冲产生了干扰。这时不能认为直射径和反射径的信号为同一径的信号。当脉冲周期进一步缩短，从而相应的信号频带进一步增大时，频率选择性衰落更加严重。可想而知，在更多反射径存在的情况下，码间干扰将更加严重。

到此，你应该了解了多径信道与瑞利衰落和频率选择性衰落的关系。信道的时变性下面载继续整理。