机器学习基础概念：查准率、查全率、ROC、混淆矩阵、F1-Score 机器学习实战：分类器

查准率、查全率

对于二分类问题，可将样例根据其真实类别与学习器预测类别的组合划分为真正例TP、假正例FP、真反例TN、假反例FN四种，令TP、FP、TN、FN分别表示其对应的样例数，则显然有TP+FP+TN+FN=样例总数，分类结果的“混淆矩阵”为：

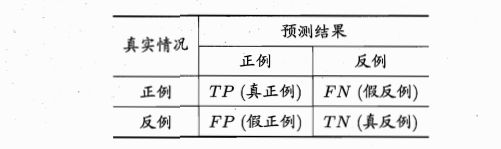
查准率P：
$$p=\frac{TP}{TP+FP}$$
查全率R：
$$R=\frac{TP}{TP+FN}$$
查准率和查全率是一对矛盾的度量，一般来说，查准率高时，查全率往往偏低；而查全率高时，查准率往往偏低。
我们可以根据学习器的预测结果对样例进行排序，排在前面的是学习器认为“最可能”是正例的样本，排在最后的是学习器认为“最不可能”是正例的样本，按此顺序逐个将样本作为正例进行预测，则每次都可以计算出当前的查全率、查准率。以查准率为纵轴，查全率为横轴作图就得到了“P-R曲线”，下面给出P-R曲线与平衡点的示意图：

还能根据P-R曲线判断学习器的性能优劣，一般用P-R曲线在坐标中的面积来比较，但是计算过程还是比较麻烦的。

F1-Score、ROC、混淆矩阵

混淆矩阵：在机器学习领域和统计分类问题中，混淆矩阵（英语：confusion matrix）是可视化工具，特别用于监督学习，在无监督学习一般叫做匹配矩阵。矩阵的每一列代表一个类的实例预测，而每一行表示一个实际的类的实例。之所以如此命名，是因为通过这个矩阵可以方便地看出机器是否将两个不同的类混淆了（比如说把一个类错当成了另一个）。混淆矩阵（也称误差矩阵）是一种特殊的, 具有两个维度的（实际和预测）列联表，并且两维度中都有着一样的类别的集合
F1-Score：F1是基于查准率和查全率的调和平均定义的：
$$\frac{1}{F1}=\frac{1}{2}(\frac{1}{P}+\frac{1}{R})$$
$$F1=\frac{2PR}{P+R}=\frac{2TP}{样例总数+TP-TN}$$
在实际应用中，由于对查准率和查全率的重视程度不同，所以会对两者有不同的偏好，所以F1度量的一般形式——$F_{\beta }$，能够表达出对查准率或查全率的不同偏好。
$$F_{\beta }=\frac{(1+{\beta }^2)PR}{({\beta }^{2}P)+R}$$
其中$\beta >0$度量了 查全率对查准率的相对重要性。$\beta =1$时退化为标准的F1;$\beta >1$时查全率有更大影响，$\beta <1$时查准率有更大影响。
ROC：是“受试者工作特征”曲线，根据学习器的预测结果对样例进行排序，按照这个顺序逐个把样本作为正例进行预测，每次计算出两个重要量的值，分别以它们为横、纵坐标作图，就得到了“ROC曲线”，ROC曲线的纵轴是“真正例率（TPR）”，横轴是“假正例率（FPR）”
$$TPR=\frac{TP}{TP+FN}FPR=\frac{FP}{TN+FP}$$
给定一个二元分类模型和它的阈值，就能从所有样本的真实值和预测值计算出一个 (X=FPR, Y=TPR) 座标点。将同一模型每个阈值 的 (FPR, TPR) 座标都画在ROC空间里，就成为特定模型的ROC曲线

机器学习实战：分类器

首先从简单的开始，训练一个二分器，只尝试识别一个数字，只能区分两种类别：是这个数字和不是这个数字。以5为例
首先创建目录标量：

y_train_5=(y_train==5)
y_test_5=(y_test==5)

然后挑选分类器，一般比较好的是选择一个随机梯度下降（SGD）分类器，使用的是sklearn的SGDlassifier类。它的优势就是能够有效处理非常大型的数据集，SGD独立处理训练实例，一次运行一个

from sklearn.linear_model import SGDClassifier
sgd_clf=SGDClassifier(max_iter=5,tol=-np.infty,random_state=42)
sgd_clf.fit(X_train,y_train_5)
sgd_clf.predict([some_digit])

运行结果：

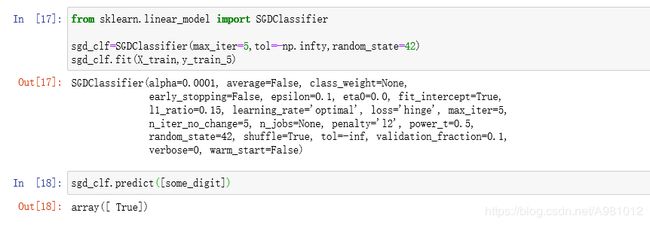
然后对分类器进行性能考核，有许多性能考核的方法。

性能考核方法：使用交叉验证测量精度

使用随机交叉验证：

from sklearn.model_selection import cross_val_score
cross_val_score(sgd_clf, X_train, y_train_5, cv=3, scoring="accuracy")

运行结果：

使用分层交叉验证:

# 类似于分层采样，每一折的分布类似
from sklearn.model_selection import StratifiedKFold
from sklearn.base import clone

skfolds = StratifiedKFold(n_splits=3, random_state=42)
for train_index, test_index in skfolds.split(X_train, y_train_5):
    clone_clf = clone(sgd_clf)
    X_train_folds = X_train[train_index]
    y_train_folds = (y_train_5[train_index])
    X_test_fold = X_train[test_index]
    y_test_fold = (y_train_5[test_index])

    clone_clf.fit(X_train_folds, y_train_folds)
    y_pred = clone_clf.predict(X_test_fold)
    n_correct = sum(y_pred == y_test_fold)
    print(n_correct / len(y_pred))

运行结果：

可以看到这两种交叉验证的准确率都是比较高的。
然后我们将所有图片都预测为‘非5’，使用随机预测模型

from sklearn.base import BaseEstimator
# 随机预测模型
class Never5Classifier(BaseEstimator):
    def fit(self, X, y=None):
        pass
    def predict(self, X):
        return np.zeros((len(X), 1), dtype=bool)
never_5_clf = Never5Classifier()
cross_val_score(never_5_clf, X_train, y_train_5, cv=3, scoring="accuracy")

运行结果：

可以看出这三种验证方式的准确率都是高于百分之九十的，所有准确率通常无法成为分类器的首要性能指标。

性能考核方法：混淆矩阵

评估分类器性能的更好的方法是混淆矩阵，就是统计A类别实例被分成B类别的次数。例如，要想知道分类器将数字3和数字5混淆多少次，只需要通过混淆矩阵的第5行第3列来查看。
要计算混淆矩阵，需要一组预测才能将其与实际目标进行比较。可以使用cross_val_predict()函数。
cross_val_predict（）和 cross_val_score（） 不同的是，前者返回预测值，并且是每一次训练的时候，用模型没有见过的数据来预测

from sklearn.model_selection import cross_val_predict
from sklearn.metrics import confusion_matrix
y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3)
confusion_matrix(y_train_5, y_train_pred)

运行结果：

上面的结果表明：第一行所有’非5’(负类)的图片中,有53417被正确分类(真负类)，1162，错误分类成了5(假负类)；第二行表示所有’5’（正类）的图片中，有1350错误分类成了非5(假正类)，有4071被正确分类成5(真正类).
一个完美的分类器只有真正类和真负类，所以其混淆矩阵只会在其对角线(左上到右下)上有非零值

混淆矩阵能提供大量信息，但有时我们可能会希望指标简洁一些。正类预测的准确率是一个有意思的指标,它也称为分类器的精度(如下)。
$$Precision(精度)=\frac{TP}{TP+FP}$$
其中TP是真正类的数量，FP是假正类的数量。
做一个简单的正类预测，并保证它是正确的，就可以得到完美的精度(精度=1/1=100%)
这并没有什么意义，因为分类器会忽略这个正实例之外的所有内容。因此，精度通常会与另一个指标一起使用，这就是召回率，又称为灵敏度或者真正类率(TPR)：它是分类器正确检测到正类实例的比率(如下):
$$Recall(召回率)=\frac{TP}{TP+FN}$$
FN是假负类的数量

精度和召回率

使用sklearn的工具可以度量精度和召回率，可以将精度和召回率组合成单一的指标，为F1-Score。F1分数对于有相近的精度和召回率的分类器更有例，但是也只是一般情况，我们在某些情况下是会对精度和召回率有所偏好的，所以我们要进行精度/召回率权衡。
在分类中，对于每一个实例，都会计算出一个分值，同时也有一个阈值，大于为正例，小于为负例，通过调节这个阈值，可以调整精度和召回率

from sklearn.metrics import precision_recall_curve
y_scores = sgd_clf.decision_function([some_digit])
precisions, recalls, thresholds = precision_recall_curve(y_train_5, y_scores)
def plot_precision_recall_vs_threshold(precisions, recalls, thresholds):
    plt.plot(thresholds, precisions[:-1], "b--", label="Precision", linewidth=2)
    plt.plot(thresholds, recalls[:-1], "g-", label="Recall", linewidth=2)
    plt.xlabel("Threshold", fontsize=16)
    plt.title("精度和召回率VS决策阈值", fontsize=16)
    plt.legend(loc="upper left", fontsize=16)
    plt.ylim([0, 1])

plt.figure(figsize=(8, 4))
plot_precision_recall_vs_threshold(precisions, recalls, thresholds)
plt.xlim([-700000, 700000])
plt.show()

结果显示：

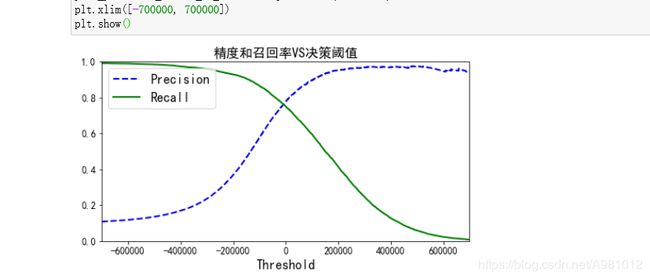
可以看到，随着阈值的提高，召回率下降了。
找到最好的精度/召回率权衡的方法是直接绘制精度和召回率的函数图

def plot_precision_vs_recall(precisions, recalls):
    plt.plot(recalls, precisions, "b-", linewidth=2)
    plt.xlabel("Recall", fontsize=16)
    plt.title("精度VS召回率", fontsize=16)
    plt.ylabel("Precision", fontsize=16)
    plt.axis([0, 1, 0, 1])

plt.figure(figsize=(8, 6))
plot_precision_vs_recall(precisions, recalls)
plt.show()

运行结果：

可以根据实际情况来选择一个精度/召回率权衡。

ROC曲线

ROC曲线绘制的是灵敏度和(1-TNR）的关系
使用roc_curve()函数计算多种阈值的TPR和FPR

# 使用 roc_curve()函数计算多种阈值的TPR和FPR
from sklearn.metrics import roc_curve

fpr, tpr, thresholds = roc_curve(y_train_5, y_scores)
def plot_roc_curve(fpr, tpr, label=None):
    plt.plot(fpr, tpr, linewidth=2, label=label)
    plt.plot([0, 1], [0, 1], 'k--')
    plt.axis([0, 1, 0, 1])
    plt.xlabel('False Positive Rate', fontsize=16)
    plt.ylabel('True Positive Rate', fontsize=16)

plt.figure(figsize=(8, 6))
plot_roc_curve(fpr, tpr)
plt.show()

运行结果：

虚线表示纯随机的ROC曲线。
有一种比较分类器的方式是测量曲线下的面积（AUC）。完美的ROC AUC等于1，纯随机分类的ROC AUC等于0.5

from sklearn.metrics import roc_auc_score
roc_auc_score(y_train_5, y_scores

运行结果：

得到AUC的值为0.956
ROC曲线和精度/召回率曲线非常相似。当正类非常少见或者你更关注假正类而不是假负类时，应该选择PR曲线，反之选择ROC曲线。
例如，看前面的ROC曲线图时，以及ROC AUC分数时，你可能会觉得分类器真不错。但这主要是应为跟负类(非5)相比，正类(数字5)的数量真的很少。相比之下，PR曲线清楚地说明分类器还有改进的空间(曲线还可以更接近右上角)

训练一个随机森林分类器，并计算ROC和ROC AUC分数

# 具体RF的原理，第七章介绍
from sklearn.ensemble import RandomForestClassifier
forest_clf = RandomForestClassifier(n_estimators=10, random_state=42)
y_probas_forest = cross_val_predict(forest_clf, X_train, y_train_5, cv=3,
                                    method="predict_proba")
y_scores_forest = y_probas_forest[:, 1] # score = proba of positive class
fpr_forest, tpr_forest, thresholds_forest = roc_curve(y_train_5,y_scores_forest)
plt.figure(figsize=(8, 6))
plt.plot(fpr, tpr, "b:", linewidth=2, label="SGD")
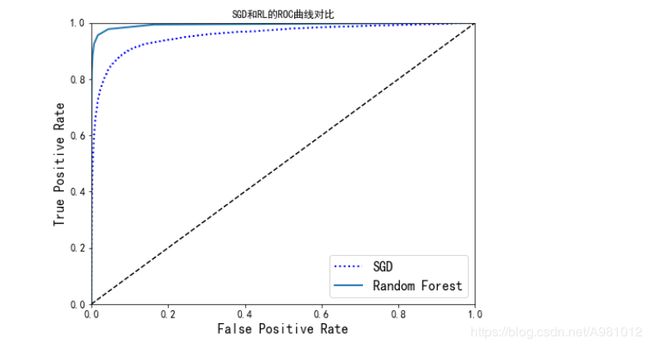
plot_roc_curve(fpr_forest, tpr_forest, "Random Forest")
plt.title("SGD和RL的ROC曲线对比")
plt.legend(loc="lower right", fontsize=16)
plt.show()
roc_auc_score(y_train_5, y_scores_forest)
#测量精度和召回率
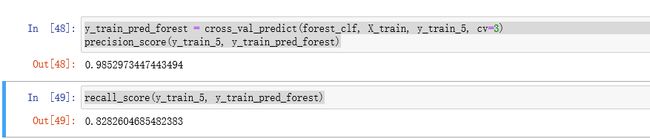
y_train_pred_forest = cross_val_predict(forest_clf, X_train, y_train_5, cv=3)
precision_score(y_train_5, y_train_pred_forest)
recall_score(y_train_5, y_train_pred_forest)

运行结果：


下面是计算的精度和召回率

参考文献：机器学习_周志华 第二章、模型评估与选择、
第一部分-机器学习基础+第三章-分类

如有错误请指正！