绘制几何图形，生成辅助线的思路

目录

辅助线的概念

绘制线规则

捕捉辅助线的思路

生成辅助线的思路

总结

---

在实际绘制几何图形过程时，有几个工具比较实用：

1. 鼠标绘制时，焦点捕捉已绘制图形的端点、线段上；
2. 撤销与回退
3. 辅助线

焦点捕捉的功能的思路相对比较简单，不断地比较当前鼠标所在的屏幕像素点为圆心，R为半径的搜索圆与绘制图形的端点和线段是否相交的问题。但在实时的图形编程的难点在于细节，至于如何优化搜索的速度，有很多方法，涉及比较深的图形搜索方法，比如对所有的图形空间先建立R树空间索引，这里不做详细介绍。

撤销与回退的功能则更加简单，其实就是状态管理，入栈和出栈的问题。

接下来，我们讲述一下在绘制过程中是辅助线的实现思路

辅助线的概念

辅助线分为静态辅助线和动态辅助线。

• 静态辅助线是指一直摆放在屏幕上不动的辅助线，鼠标能捕捉到上面，比如PS的辅助线。

• 动态辅助线是指在绘制过程中，根据已绘制的内容，智能的生成辅助线，并能让鼠标捕捉到上面

绘制线规则

1. 鼠标在移动过程中，在指定的阈值范围内能捕捉到辅助线上的最近的点
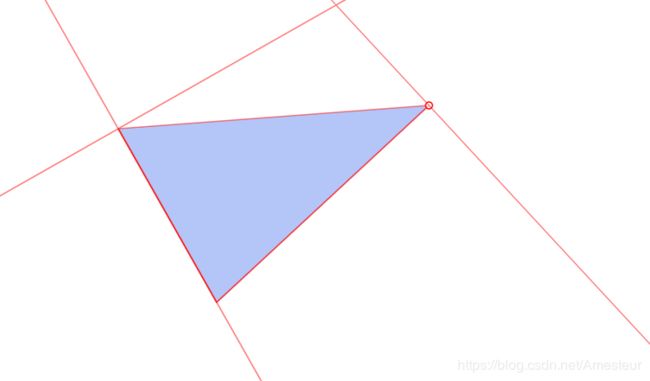
2. 每次绘制端点后，能够根据新生成的端点，生成一条相同方向和正交（相互垂直）的辅助线（根据需要生成指定角度的辅助线）
3. 在绘制完成后，清除辅助线。

 

 

捕捉辅助线的思路

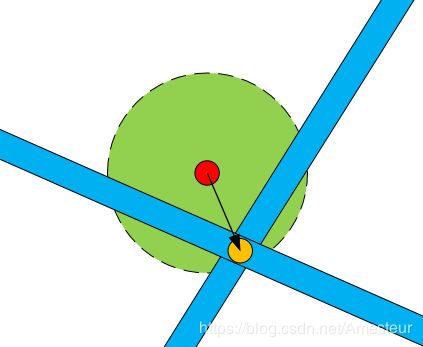
鼠标在屏幕移动过程中，在辅助线附近时，能够捕捉到辅助线是指鼠标的绘制焦点能自动移动到辅助线上，实际移动的是绘制焦点而不是鼠标点。而实现捕捉到辅助线，需要以下两步：

1. 计算当前绘制焦点与辅助线的最短距离是否少于定义的阈值A（A是一个相对于比较小的值），若少于阈值A，则绘制焦点设置为辅助线上离当前绘制焦点最近的点。

因此，关键的地方，在于获取点到线段的最近的点，以及点与点之间的距离。核心代码如下：

/**
 * @desc 此方法既获取点到多段连续的线段中最近的点，以及返回最短的距离
 * @param {Array} coordinates 多段连续的线段的坐标数组.[x1,y1,x2,y2,x3,y3...]
 * @param {number} offset 起始点的索引偏移量.
 * @param {number} end 终点的索引.
 * @param {number} stride 坐标所占的个数，二维图形为2.
 * @param {number} maxDelta 多段连续的线段中每两个相邻点中最长的那一段的距离的平方.
 * @param {boolean} isRing 是否是环, 线段是否闭合.
 * @param {number} x 目标点的x坐标.
 * @param {number} y 目标点的y坐标
 * @param {Array} closestPoint 输出的最近的点的对象.
 * @param {number} [minSquaredDistance=Infinity] 最小的垂直距离，用于较少比较.默认Infinity
 * @return {number} 点到多段连续的线段中最短的距离.
 */
function assignClosestPoint(coordinates, offset, end, stride, 
    maxDelta, isRing, x, y, closestPoint, minSquaredDistance) {
  if (offset == end) { // 如果起点的索引和终点索引的一致，表示参数错误
    return minSquaredDistance;
  }
  let i, squaredDistance;
  if (maxDelta === 0) { // 如果最大的相邻点间的距离为0，表示线段各个点为同一个点
    // 所有点都相同，所以只需测试第一点
    squaredDistance = squaredDx( // squaredDx方法获取两点之间的垂直距离的平方
      x, y, coordinates[offset], coordinates[offset + 1]);

    if (squaredDistance < minSquaredDistance) { // 如果绘制焦点与线段第一个点的距离少于定义的最小距离，则最近的点为线段的第一个点
      for (i = 0; i < stride; ++i) {
        closestPoint[i] = coordinates[offset + i];
      }
      closestPoint.length = stride;
      return squaredDistance;
    } else {
      return minSquaredDistance;
    }
  }
  const tmpPoint = [NaN, NaN]; // 用于临时存储点到线段的最近的点
  let index = offset + stride;
  while (index < end) {
    assignClosest( // assignClosest方法是获取点到其中一段线段(只有两个坐标构成的线段)
      coordinates, index - stride, index, stride, x, y, tmpPoint); 
    squaredDistance = squaredDx(x, y, tmpPoint[0], tmpPoint[1]); //得到目标点到任意一个线段的最短距离的平方
    if (squaredDistance < minSquaredDistance) {
      minSquaredDistance = squaredDistance;
      for (i = 0; i < stride; ++i) {
        closestPoint[i] = tmpPoint[i];
      }
      closestPoint.length = stride;
      index += stride;
    } else {
      // 跳过多个点，因为我们知道所有跳过的点都不能比我们找到的最近点更近。我们知道这是因为我们知
      // 道当前点有多近，到目前为止我们找到的最近点有多近，以及连续点之间的最大距离。例如，如果我
      // 们当前的最近点距离是10，那么到目前为止我们发现的最好的距离是3，并且连续点之间的最大距离是2，
      // 那么我们需要跳过至少（10-3）/2==3（向下取整）点，以便有机会找到更近的点。我们使用
      // math.max（…，1）来确保我们总是前进至少一个点，以避免无限循环。.
      index += stride * Math.max(
        ((Math.sqrt(squaredDistance) -
            Math.sqrt(minSquaredDistance)) / maxDelta) | 0, 1);
    }
  }
  if (isRing) {
    // 如果是环的话，则还需要检查最后的闭合的那一段线段
    assignClosest(
      coordinates, end - stride, offset, stride, x, y, tmpPoint);
    squaredDistance = squaredDx(x, y, tmpPoint[0], tmpPoint[1]);
    if (squaredDistance < minSquaredDistance) {
      minSquaredDistance = squaredDistance;
      for (i = 0; i < stride; ++i) {
        closestPoint[i] = tmpPoint[i];
      }
      closestPoint.length = stride;
    }
  }
  return minSquaredDistance;
}
  /**
   * @desc 计算距离
   * @param {*} p1 起始点
   * @param {*} p2 终结点
   */
  function dist2D (p1, p2) {
    var dx = p1[0] - p2[0]
    var dy = p1[1] - p2[1]
    return Math.sqrt(dx * dx + dy * dy)
  }

2. 上述第一个点是针对，只有一条辅助线满足条件的情况。若存在，多条辅助线满足，绘制焦点到辅助线的距离少于阈值A，则取任意两条辅助的焦点作为最新的绘制焦点。（因为阈值A比较小，可以默认其差别不大）

关键在于，求取两个线段的交点，关键代码如下：

  /**
   * @description 根据两条线段的端点，得到线段相交的点
   * @param {*} d1 线段1的两个端点坐标
   * @param {*} d2 线段2的两个端点坐标
   */
  function getIntersectionPoint (d1, d2) {
    var d1x = d1[1][0] - d1[0][0]
    var d1y = d1[1][1] - d1[0][1]
    var d2x = d2[1][0] - d2[0][0]
    var d2y = d2[1][1] - d2[0][1]
    var det = d1x * d2y - d1y * d2x

    if (det !== 0) {
      var k = (d1x * d1[0][1] - d1x * d2[0][1] - d1y * d1[0][0] + d1y * d2[0][0]) / det
      return [d2[0][0] + k * d2x, d2[0][1] + k * d2y]
    } else return false
  }

上述的距离，一般指的是屏幕像素坐标的距离。

最后，焦点不断捕捉的过程是实时的，因此，当鼠标移动过程中需要不断地执行上述的两个步骤。因此，调优是需要下点功夫的。

生成辅助线的思路

必须定义当绘制完成图形的某个端点时的回调方法。在回调方法中，其实根据已知的点坐标，计算辅助线的方程，并根据方程进行等距离的点插值。如下步骤：

1. 根据刚绘制的端点与上一个端点，则得到新的直线方程的斜率（辅助线是90度，45度或者延长线）及其经过的一个点（刚绘制的端点），得到辅助线方程

2. 得到直线方程后，根据直线的点向式的代数形式，以固定的距离进行插值，得到屏幕上的辅助线。

/** 新增辅助线
* @param {Array} v 坐标数组，只有两个断电
* @return {*} 辅助线对象
*/
function addGuide (v, ortho) {
  if (v) {
    const guideLength = Math.max(
      this.projExtent_[2] - this.projExtent_[0],
      this.projExtent_[3] - this.projExtent_[1]
    )// 从定义的最大空间范围中获取辅助线的最大长度

    const extent = this.projExtent_// 获取最大空间范围

    const dx = v[0][0] - v[1][0] 
    const dy = v[0][1] - v[1][1]
    const d = 1 / Math.sqrt(dx * dx + dy * dy)

    const generateLine = function (/** 方向 **/loopDir) {
      var p, g = []
      var loopCond = guideLength * loopDir * 2
      for (var i = 0; loopDir > 0 ? i < loopCond : i > loopCond; i += (guideLength * loopDir) / 4) { // 插值100个等距离的点
        if (ortho) p = [v[0][0] + dy * d * i, v[0][1] - dx * d * i]
        else p = [v[0][0] + dx * d * i, v[0][1] + dy * d * i]
        // 判断插值的点是否在最大的extent里
        if (containsCoordinate(extent, p)) g.push(p)
        else break
      }
      return new LineString([g[0], g[g.length - 1]]))
    }

    var f0 = generateLine(1)// 正向辅助线
    var f1 = generateLine(-1)// 反向辅助线

    return [f0, f1]
  }
}

总结

绘制辅助线是一个实时性比较强的功能，原理是简单的几何拓扑知识。实现起来比较简单，几何的实时拓扑难点在于性能调优，选择合适的策略去实现功能。