卷积操作、填充和步幅以及池化

本文主要是学习了Dive-into-DL-PyTorch这本书。因此这篇博客的大部分内容来源于此书。框架使用的是pytorch，开发工具是pycharm
参考 动手学深度学习Dive-into-DL-Pytorch
参考链接 https://github.com/ShusenTang/Dive-into-DL-PyTorch
https://github.com/zergtant/pytorch-handbook
https://www.cnblogs.com/xiaojianliu/articles/9904365.html

卷积操作

卷积运算：对应元素相乘再相加。卷积窗口（核数组）从输入数组最左上方开始，按从左往右、从上往下的顺序，依次在输入数组上滑动。当卷积窗口滑动到某一位置时，窗口中的输入子数组与核数组按元素相乘并求和，得到输出数组中相应位置的元素。
卷积操作的代码实现

def corr2d(X, K):
    h, w = K.shape
    Y = torch.zeros((X.shape[0] - h + 1, X.shape[1] - w + 1))
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            Y[i, j] = (X[i: i + h, j: j + w] * K).sum()
    return Y

二维卷积层
卷积层的模型参数包括了卷积核和标准偏差。在训练模型的时候，通常先对卷积核随机初始化，然后不断迭代卷积核和偏差。

自己理解：在卷积层中，卷积核只需要定义形状是因为在进行卷积运算的时候是输入和权重进行卷积运算，而传入卷积核的大小只不过是为了初始化一个随机的但形状与卷积核形状相同的权重张量。然后在每一次的训练过程中不断更新权重张量，最后让权重张量学到一定的特征。说白了就是权重参数和输入做卷积运算，然后再加上偏置值

import torch
from torch import nn
#卷积操作
def corr2d(X, K):
    h, w = K.shape
    Y = torch.zeros((X.shape[0] - h + 1, X.shape[1] - w + 1))
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            Y[i, j] = (X[i: i + h, j: j + w] * K).sum()
    return Y
    
#卷积层
class Conv2D(nn.Module):
    def __init__(self, kernel_size):
        super(Conv2D, self).__init__()
        self.weight = nn.Parameter(torch.randn(kernel_size))
        self.bias = nn.Parameter(torch.randn(1))
    def forward(self, x):
        return corr2d(x, self.weight) + self.bias

#模拟数据
X = torch.ones(6, 8)
X[:, 2:6] = 0
K = torch.tensor([[1, -1]])  #卷积核
Y = corr2d(X, K) #Y是真实的标签，通过一次卷积操作得到，是X和K的卷积运算
# 构造一个核数组形状是(1, 2)的二维卷积层
conv2d = Conv2D(kernel_size=(1, 2))
step = 20
lr = 0.01
for i in range(step):
    Y_hat = conv2d(X)
    l = ((Y_hat - Y) ** 2).sum()
    l.backward()
    # 梯度下降,更新卷积层的权重和偏置值
    conv2d.weight.data -= lr * conv2d.weight.grad
    conv2d.bias.data -= lr * conv2d.bias.grad
    # 梯度清零
    conv2d.weight.grad.fill_(0)
    conv2d.bias.grad.fill_(0)
    if (i + 1) % 5 == 0:
        print('Step %d, loss %.3f' % (i + 1, l.item()))

print("weight: ", conv2d.weight.data)
print("bias: ", conv2d.bias.data)

结果：

Step 5, loss 8.376
Step 10, loss 1.121
Step 15, loss 0.177
Step 20, loss 0.034
weight:  tensor([[ 0.9748, -0.9463]])
bias:  tensor([-0.0159])

所以最后权重通过20次的迭代后，参数值应该与K的参数值很接近（相当于此次的数据如果把20次后的权重参数看做是标签值，则K就是它的真实值）可以看到，学到的卷积核的权重参数与之前定义的核数组K较接近，而偏置参数接近0。

填充

假设输入形状是nhxnw,卷积核窗口形状是khxkw，那么输出形状则是 (nh-kh+1)x(nw-kw+1)
填充（padding）是指在输入高和宽的两侧填充元素（通常填充0）。如图所示，在原输入高和宽的两侧分别添加值为0 的元素，是的输入的高和宽从3变成了5，并导致输出的高和宽由2增到4。

一般来说，如果在高的两侧一共填充ph行，在宽的两侧一共填充pw列，那么输出的形状将会是
(nh-kh+ph+1)x(nw-kw+pw+1) 也就是说，输出的高和宽会分别增加ph和pw。
在很多情况下，会设置ph=kh-1和pw=kw-1来使输入和输出具有相同的高和宽。这样会方便在构造网络时推测每个层的输出形状。当kh是奇数的时候，会在高的两侧分别填充ph/2行。当kh是偶数的时候，一种可能是在输入的顶端一侧填充 ph/2向上取整行，而在底端一侧填充ph/2向下取整行。（例如：7.4向下取整就是7；向上取整就是8）。在宽的两侧填充原理相同。
注：
数学中向上取整和向下取整符号：

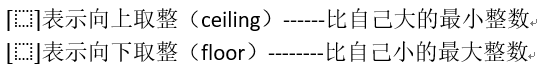
步幅

卷积窗口（核数组）从输入数组最左上方开始，按从左往右、从上往下的顺序，依次在输入数组上滑动。将每次滑动的行数和列数称为步幅。

一般情况下，在高和宽两个方向上步幅均为1.也可以使用更大的步幅。如图所示，在高上的步幅为3、在宽上的步幅为2.当输出第一列的第二个元素时，卷积窗口向下滑动了3行，而在输出第一行第二个元素时卷积窗口向右滑动了2列。当卷积窗口在输入上再向右滑动2列时，由于输入元素无法填满窗口，无结果输出。

以上图片的输出计算：
输出的第一行第一列：0x0+0x1+0x2+0x3=0
输出的第一行第二列：0x0+0x1+1x2+2x3=8
输出的第二行第一列：0x0+6x1+0x2+0x3=6
输出的第二行第二列：7x0+8x1+0x2+0x3=8
注：在公式计算中ph表示高的两侧一共填充ph行，而在代码中 padding=（1,1），就高来说指的是上或者下的一侧填充ph行，两侧一共填充的是2行，即带入公式的是ph=2而不是1！！！

多输入通道

当输入数据含多个通道时，需要构造一个输入通道数与输入数据的通道数相同的卷积核。假设输入数据的通道数为ci，那么卷积核的输入通道数同样为ci。设卷积核窗口形状为khxkw。当ci=1时，卷积核只包含一个形状为khxkw的二维数组。当ci>1时，将会为每个输入通道各分配一个形状为khxkw的核数组。把这ci个数组在输入通道维上连结，即得到一个形状为cixkhxkw的卷积核。在各个通道上对输入的二维数组和卷积核的二维核数组做运算，再将这ci个运算后的二维输出按通道相加，得到一个二维数组。

多输出通道

当输入通道有多个时，因为对各个通道的结果做了累加，所以无论输入通道数是多少，输出通道数总为1。设卷积核输入通道数分别为ci和co，高和宽分别为kh和kw。如果希望得到含多个通道的输出，可以为每个输出通道分别创建形状为cixkhxkw的核数组。将它们在输出通道维度上连结，卷积核的形状即c0xcixkhxkw。在做运算时，每个输出通道上的结果由卷积核在该输出通道上的核数组与整个输入数组计算而来。
1x1卷积层
当卷积窗口形状为1x1(kh=kw=1)的多通道卷积层。实际上，1x1卷积的主要计算发生在通道维度上。注：输入和输出具有相同的高和宽。输出中的每个元素来自输入中在高和宽上相同位置的元素在不同通道之间的按权重累加。假设将通道维当作特征维，将高和宽维度上的元素当作数据的样本，那么在1x1卷积层的作用与全连接层等价。
程序实现：

import torch
from torch import nn
#对应元素相乘再相加
def corr2d(X, K):
    h, w = K.shape
    Y = torch.zeros((X.shape[0] - h + 1, X.shape[1] - w + 1))
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            Y[i, j] = (X[i: i + h, j: j + w] * K).sum()
    return Y

#多通道输入，单通道输出(只有0维一个输出通道）
def corr2d_multi_in(X, K):
 #沿着x和k的第0维（通道维）分别计算再相加
 res = corr2d(X[0, :, :], K[0, :, :])
 for i in range(1, X.shape[0]):
     res +=corr2d(X[i, :, :], K[i, :, :])
     return res
# X = torch.tensor([[[0, 1, 2], [3, 4, 5], [6, 7, 8]],
#                   [[1, 2, 3], [4, 5, 6], [7, 8, 9]]])
# K = torch.tensor([[[0, 1], [2, 3]], [[1, 2], [3, 4]]])
# out=corr2d_multi_in(X, K)
# print(out.shape)

#多通道输入多通道输出
def corr2d_multi_in_out(X, K):
  #对k的第0维遍历，每次同输入x做卷积运算。所有结果用stack函数合并
  return torch.stack([corr2d_multi_in(X, k) for k in K])

# K = torch.stack([K, K + 1, K + 2]) #将K堆叠出3通道
# K.shape  # torch.Size([3, 2, 2, 2])
# out=corr2d_multi_in_out(X, K)
# print(out.shape)

def corr2d_multi_in_out_1x1(X, K):
    c_i, h, w = X.shape
    c_o = K.shape[0]
    X = X.view(c_i, h * w) #c_i相当于是特征数，h*w是样本数
    K = K.view(c_o, c_i) #k是权重张量，c_o是输出数，c_o是特征数
    Y = torch.mm(K, X)  # 全连接层的矩阵乘法
    '''
    将参数的位置进行了调整，原先的矩阵乘法是X*W,X是样本数*特征数,W是特征数*输出数，得到的是样本数*输出数
    现在是W*X，W是输出数*特征数，X是特征数*样本数，得到的是输出数*样本数
    '''

    return Y.view(c_o, h, w)#将输出的形状转为(输出数，高，宽)
 
X = torch.rand(3, 3, 3)
K = torch.rand(2, 3, 1, 1)
Y1 = corr2d_multi_in_out_1x1(X, K)
print(Y1.shape)

池化

池化层的作用：1、保持一定范围内的不变性，包括旋转、平移、尺度的不变性。（缓解卷积层对位置的过度敏感性）
2、保持主要特征的同时减少参数（降维）

#池化
import torch
from torch import nn
def pool2d(X, pool_size, mode='max'):
    X = X.float()
    p_h, p_w = pool_size
    Y = torch.zeros(X.shape[0] - p_h + 1, X.shape[1] - p_w + 1)
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            if mode == 'max':
                Y[i, j] = X[i: i + p_h, j: j + p_w].max()
            elif mode == 'avg':
                Y[i, j] = X[i: i + p_h, j: j + p_w].mean()
    return Y

X = torch.tensor([[0, 1, 2], [3, 4, 5], [6, 7, 8]])
pool = pool2d(X, (2, 2))
print(pool)

#池化的填充和步幅
'''
默认情况下，MaxPool2d实例里步幅和池化窗口形状相同。
下面使用形状为(3,3)的池化窗口，默认获得形状为（3,3）的步幅。padding=0
'''
X = torch.arange(16, dtype=torch.float).view((1, 1, 4, 4))
pool2d = nn.MaxPool2d(3)
print(pool2d(X))
#也可以手动指定步幅和填充
pool2d = nn.MaxPool2d(3, padding=1, stride=2)
print(pool2d(X))
#也可指定非正方形的池化窗口并分别指定高和宽上的填充和步幅
pool2d = nn.MaxPool2d((2, 4), padding=(1, 2), stride=(2, 3))
print(pool2d(X))

'''
在处理多通道输入数据时，池化层对每个驶入通道分别池化，而不像卷积层那样将各通道的输入
按通道相加。这意味着池化层的输出通道数与输入通道数相等
'''
X = torch.cat((X, X + 1), dim=1)
print(X.shape)
pool2d = nn.MaxPool2d(3, padding=1, stride=2)
print(pool2d(X).shape) #输出通道数仍然是2