数据挖掘项目：银行信用评分卡建模分析（上篇）

kaggle上的Give Me Some Credit一个8年前的老项目，网上的分析说明有很多，但本人通过阅读后，也发现了很多的问题。比如正常随着月薪越高，违约率会下降。但对于过低的月薪，违约率却为0等。
因此，本人写这个项目的目的是按照自己对数据的理解（可能有的地方是错的，希望大家指正），对网上相关的分析进行改进。（主要集中在数据预处理）

目录

由于整篇文章的篇幅过长，因此分为上下两部分。

• 上篇
  1. 理解数据
  2. 探索性数据分析
  3. 数据预处理
• 下篇
  4. 特征工程
  5. 构建模型
  6. 模型评估
  7. 评分卡建立

1.理解数据

项目背景

随着人们的消费观念的升级，所谓的“花明天的钱，圆今天的梦”。银行以及私营企业推出了各种各样的消费金融服务，具有代表性的是各大银行的信用卡，支付宝的花呗、京东白条，还有一些专门针对针对学生群体的平台，比如趣分期哈、分期乐之类的，把这些统称为信用卡用户。
只要涉及到金融借贷的，就有可能有坏账的存在。 每个公司都在用各种手段来降低坏账的发生，最常见的方法就是根据一定的规则，给每个用户打分进行预测，哪些用户可能会发生坏账，针对预测结果采取相应的措施。

本篇将针对历史坏账用户进行分析，分析坏账用户都有哪些特征，为后续的建模做准备。数据来自kaggle上的Give Me Some Credit根据信用评分建立原理，构建一个简易的信用评分卡模型——申请评分卡(A卡)，对用户自动评分。

数据获取

现在kaggle上获取数据好像要注册手机号，但是国外……所以，把数据的链接贴在这里了。
链接：https://pan.baidu.com/s/1jl9-r3FItlpHX-HP3-7d_A
提取码：mtq0

导入数据

# 需要导入的包
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import datetime
import scipy
%matplotlib inline
sns.set(style="ticks")
pd.set_option("display.max_columns",None)#展示所有列数据
pd.set_option("display.max_rows",None)#展示所有行数据
# 画图显示中文
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus'] = False
from sklearn.ensemble import RandomForestRegressor as rfr
from imblearn.over_sampling import SMOTE
from sklearn.linear_model import LogisticRegression as LR
import scikitplot as skplt

train = pd.read_csv('./cs-training.csv',index_col=0)
test = pd.read_csv('./cs-test.csv',index_col=0)

查看数据基本信息

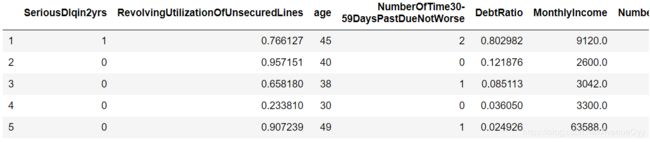
train.head()

注：对测试数据也做同样的操作，这里只举例训练数据。

train.shape
(150000, 11)
test.shape
(101503, 11)

训练集数据150000个样本，11个特征。
测试集数据101503个样本，11个特征。

数据特征含义

• SeriousDlqin2yrs -----出现 90 天或更长时间的逾期行为（即定义好坏客户）
• RevolvingUtilizationOfUnsecuredLines ----- 贷款以及信用卡可用额度与总额度比例
• age ----- 借款人借款年龄
• NumberOfTime30-59DaysPastDueNotWorse----- 过去两年内出现35-59天逾期但是没有发展得更坏的次数
• DebtRatio----- 每月偿还债务，赡养费，生活费用除以月总收入
• MonthlyIncome -----月收入
• NumberOfOpenCreditLinesAndLoans -----开放式贷款和信贷数量
• NumberOfTimes90DaysLate -----过去两年内出现90天逾期或更坏的次数
• NumberRealEstateLoansOrLines -----抵押贷款和房地产贷款数量，包括房屋净值信贷额度
• NumberOfTime60-89DaysPastDueNotWorse -----过去两年内出现60-89天逾期但是没有发展得更坏的次数
• NumberOfDependents -----家庭中不包括自身的家属人数（配偶，子女等）

查看描述统计信息

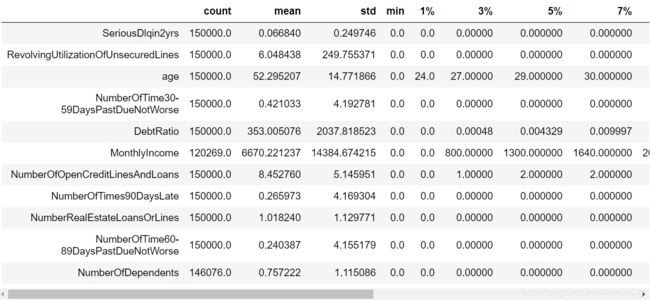
train.describe([0.01,0.03,0.05,0.07,0.1,0.25,.5,.75,.9,.99]).T

通过以上数据描述性信息可以看出：

• 有多个特征存在异常值。比如贷款额度与总额度比例存在大于1甚至几千的情况最大值为50708。年龄最小值为0，最大值为109的情况等等。这些异常值在数据探索性分析中将逐个进行说明。
• 多个特征存在有偏分布。比如贷款额度与总额度，月薪，负债率等特征。

train.info()

通过以上数据信息可以看出：

• 数据类型都为int或float，说明都是数值型的数据。
• 月薪和家属人数存在空缺值。

2.探索性数据分析

这是之前写的数据探索性分析，在分析时可以当做个参考，提供些思路。

目标特征分析：好坏客户特征

figure,ax = plt.subplots(figsize=(12,4))
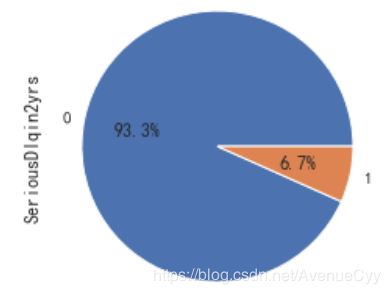
train['SeriousDlqin2yrs'].value_counts().plot.pie(autopct='%1.1f%%')
plt.show()

• 正样本（好客户）占比93.3%，负样本（坏客户）占比6.7%。说明客户一般为好客户。我们需要捕捉的是坏客户，但由于比例太过悬殊，此时样本不平衡，需要后续进行处理。

贷款额度与总额度比例

fig= plt.figure(figsize=(14,4))
ax1=fig.add_subplot(1,2,1)
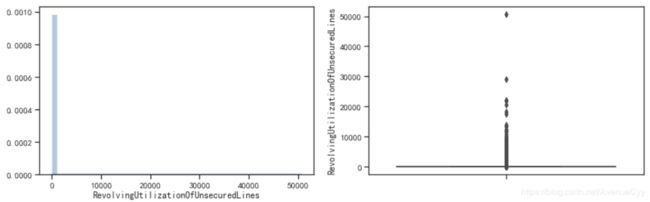
sns.distplot(train['RevolvingUtilizationOfUnsecuredLines'],kde=True)
ax1=fig.add_subplot(1,2,2)
sns.boxplot(y=train['RevolvingUtilizationOfUnsecuredLines'])
plt.show()

• 样本分布极度不平衡。大部分的值都在“0左右”，存在大量的异常数据。需要进行进一步的分析。
• 而这些异常数据可能是由于没有除以总额度造成的，或是别的一些情况。这就需要借助具体的业务进行分析。

一般认为贷款额度与总额度比例小于1是合理的情况。因此先分析比例小于时，贷款额度与总额度比例和好坏客户之间的关系。

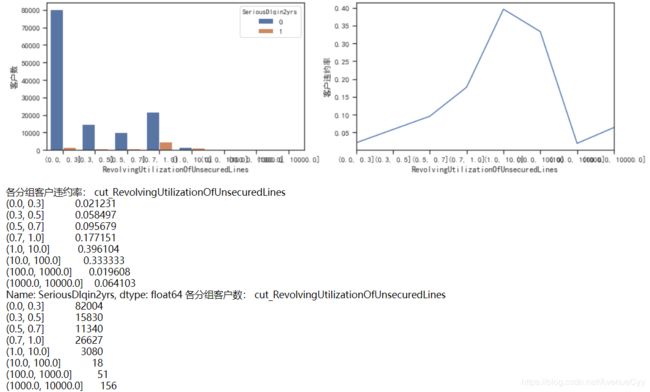
cut_num=[0,0.3,0.5,0.7,1,10,100,1000,10000]
get_compare_plot(train,feature_plot="RevolvingUtilizationOfUnsecuredLines",cut_num=cut_num,is_qcut=False)

• 这里可以看到，当Revol(贷款额度与总额度比例) 小于1时，随着该比例的增加，客户违约率也在增加，符合业务逻辑。正常来说，应该是随着比例的增加，客户违约率也会增加，但是在大于1后，该规律发生了改变，因此对其进行进一步分析。

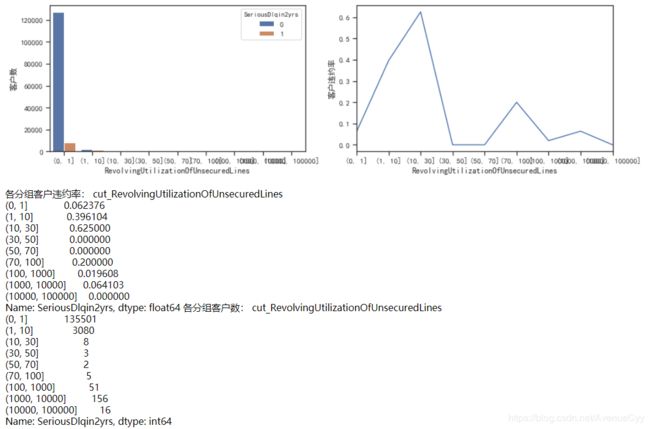
cut_num=[0,1,10,30,50,70,100,1000,10000,100000]
get_compare_plot(train,feature_plot="RevolvingUtilizationOfUnsecuredLines",cut_num=cut_num,is_qcut=False)

• 这里主要分析Revol大于10是什么情况。通过图像和数据可以发现，当比例大于10后，客户违约率在10~30达到高峰，然后下降，再往后的比例都差不多，上下浮动。
• 出现这个情况，此时要做的就是找到阈值，能分割正常值和异常值的阈值。我们可以认定10~30是一个分界点，因为它的违约率非常高，但是要注意，10-30这个区间内，客户数只有8人，随机性太大，因此不做考虑。发现1-10这个区间内的样本数足够，并且违约率也在上升，因此进一步分析。

cut_num=[]
for i in np.arange(-1,11,1):
    cut_num.append(i)
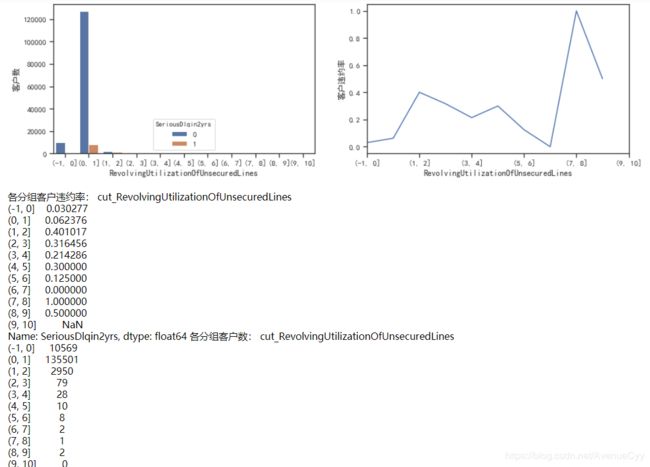
get_compare_plot(train,feature_plot="RevolvingUtilizationOfUnsecuredLines",cut_num=cut_num,is_qcut=False)

• 对1-10分析后，可以看到，在数据量足够的情况下（大于30），即1-4，违约率是在逐渐下降的，这不符合正常的规律性，应该是Revol越大，违约率越大。
• 我们发现在1-2时，违约率有了特别大的提升，从0.06到0.4。因此，可以认为阈值在这个区间内。

cut_num=[]
for i in np.arange(0.6,3.2,0.2):
    cut_num.append(i)
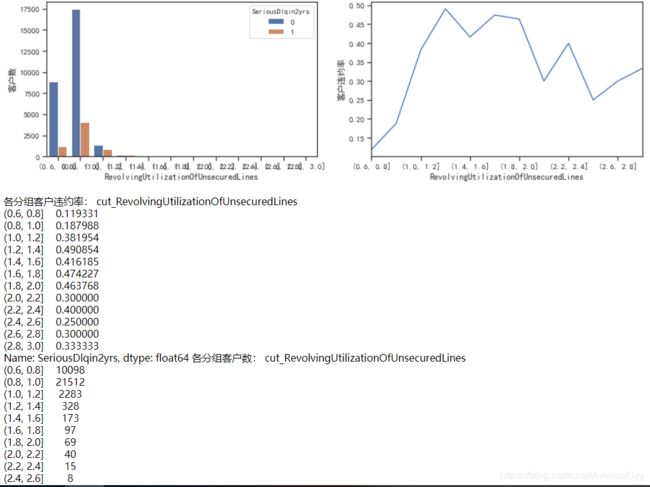
get_compare_plot(train,feature_plot="RevolvingUtilizationOfUnsecuredLines",cut_num=cut_num,is_qcut=False)

• 之间对0-1之间做过分析，因此从0.6开始。
• 通过和之前的分析对比来看，Revol在0~2内，违约率增加。超过2之后，客户数量迅速下降和违约率也有降低的趋势。因此，可以认为Revol=2，是我们要找的阈值。大于2的为异常值，小于2的为正常值。

print("贷款以及信用卡可用额度与总额度比例大于2的比重为：",100*(train['RevolvingUtilizationOfUnsecuredLines']>2).sum()/len(train),"%")

贷款以及信用卡可用额度与总额度比例大于2的比重为： 0.24733333333333332 %

• 大于2的异常值，我们可以删除。如下其占比非常低0.247%。也可以融到0~2的数据内。想到的方法有两个：一是对大于2的值统一进行缩放；二是分组，直接把大于2的值分组到0-1内。这里采用第二种分箱的方法，因为分箱的一个特点就是可以用来处理异常值。

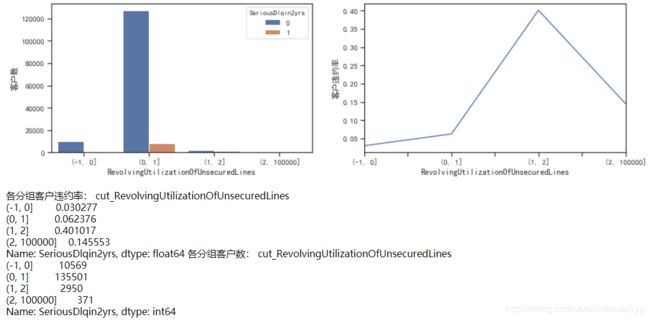
cut_num=[-1,0,1,2,100000]
get_compare_plot(train,feature_plot="RevolvingUtilizationOfUnsecuredLines",cut_num=cut_num,is_qcut=False)

• 大于2的样本有371个。将该组与0-1进行合并。原因有两点：一是0-1数据量大，抗随机性强。不会因为371个样本产生太大的波动。二是因为这371个样本，如果正常计算，归属于0-1的概率最大，因为0-1样本占比最大。因此与0-1组进行合并。

以上是对Revol这个特征的一个比较全面的分析，通过不断分组探索数据的阈值，找出比较适合的切分点。这里最后的数据处理，仍然存在问题，即可能会引入数据噪声，因为不清楚总额度具体值为多少。
以下的特征依旧会这么处理，分析数据的合理性，找出阈值，对异常值进行处理。

年龄

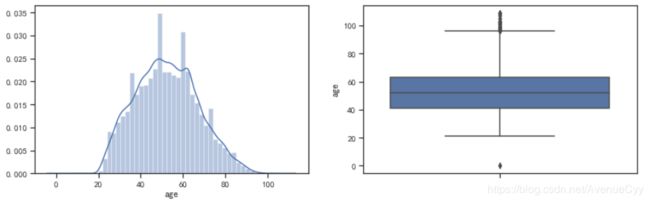
fig= plt.figure(figsize=(14,4))
ax1=fig.add_subplot(1,2,1)
sns.distplot(train['age'],kde=True)
ax1=fig.add_subplot(1,2,2)
sns.boxplot(y=train['age'])
plt.show()

• 这里年龄的分布比较接近正态分布，因此，先使用四分位差的方法来找寻异常值。（上下四分位数±1.5~3倍的四分位差）

age_mean=train['age'].mean()
age_std=train['age'].std()
age_lowlimit=age_mean-3*age_std
age_uplimit=age_mean+3*age_std
print('异常值下限：',age_lowlimit,'异常值上限：',age_uplimit)
异常值下限： 7.979609077364238 异常值上限： 96.6108042559691

• 发现年龄的下限为8岁，上限为97岁。应用四分位差的方法来找寻异常值的一个前提条件是，数据最好服从正态分布，否则会有一些偏差。这里计算一下该数据的偏度和峰度。

print('峰度：',train['age'].skew(),'偏度：',train['age'].kurt())
峰度： 0.18899454512676198 偏度： -0.4946688326403583

• 发现峰度较小，偏度为负数，SK=-0.494，SK接近-0.5，即中度左偏分布。因此，用这个四分位差去判断不是很准确。接下来对图形进行分析，进一步判断异常值。

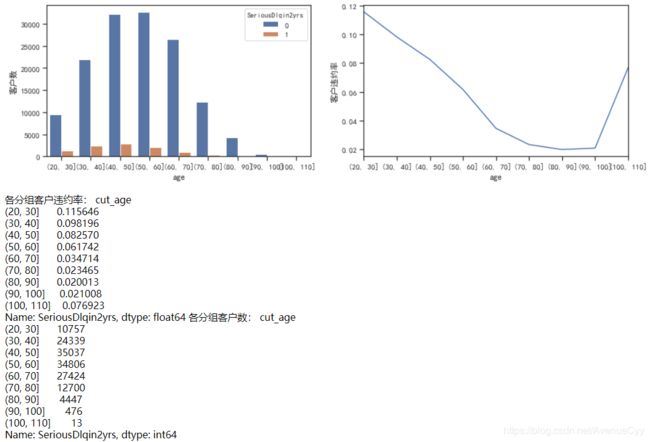
cut_num=[20,30,40,50,60,70,80,90,100,110]
get_compare_plot(train,feature_plot="age",cut_num=cut_num,is_qcut=False)

• 把年龄从20-110每10岁分一组。发现随着年龄的增加，客户违约率在逐渐降低。
  1.（年龄越大，越不容易违约）但在100-110这个阶段，违约率上升，不符合规律。
  2.年龄过大（100岁以上贷款），这种情况也比较少见。
  3.之前的97岁，由于数据非正态分布，会出现偏差。如果以100为分界点，数比较整，也好处理。
  因此，基于以上3个原因，选择100为异常值的阈值，大于100的删除。

过去两年内出现35-59天|60-89天|90天以上|逾期但是没有发展得更坏的次数

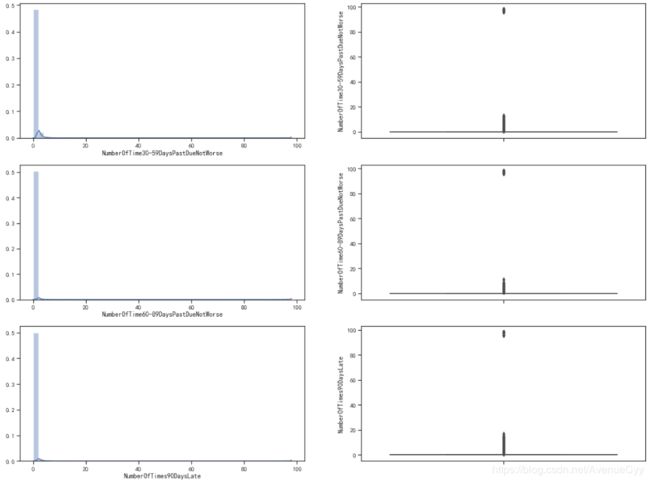
fig,[[ax1,ax2],[ax3,ax4],[ax5,ax6]] = plt.subplots(3,2,figsize=(20,15))
sns.distplot(train['NumberOfTime30-59DaysPastDueNotWorse'],ax=ax1)
sns.boxplot(y=train['NumberOfTime30-59DaysPastDueNotWorse'],ax=ax2)
sns.distplot(train['NumberOfTime60-89DaysPastDueNotWorse'],ax=ax3)
sns.boxplot(y=train['NumberOfTime60-89DaysPastDueNotWorse'],ax=ax4)
sns.distplot(train['NumberOfTimes90DaysLate'],ax=ax5)
sns.boxplot(y=train['NumberOfTimes90DaysLate'],ax=ax6)
plt.show()

• 通过分析可以发现，绝大多数值都在“0附近”，但也有次数超过80的异常值。

这里找出在限定范围内（两年内2*365），每种情况出现的最多次数。

• 30~59天24次。
• 60~89天最多的违规次数为12次。
• 90天以上最多的违规次数为8次。

print('两年内30~59天违规次数超过24次的样本数为：',(train['NumberOfTime30-59DaysPastDueNotWorse']>24).sum())
print('两年内60-89天违规次数超过12次的样本数为：',(train['NumberOfTime60-89DaysPastDueNotWorse']>12).sum())
print('两年内90天以上违规次数超过8次的样本数为：',(train['NumberOfTimes90DaysLate']>8).sum())
两年内30~59天违规次数超过24次的样本数为： 269
两年内60-89天违规次数超过12次的样本数为： 269
两年内90天以上违规次数超过8次的样本数为： 312

• 以上是训练集数据中出现的超过限定范围的样本数。将以上数据删除处理。

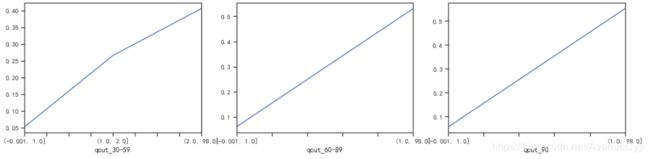
train["qcut_30-59"], updown = pd.qcut(train["NumberOfTime30-59DaysPastDueNotWorse"], retbins=True, q=20,duplicates='drop')
train["qcut_60-89"], updown = pd.qcut(train["NumberOfTime60-89DaysPastDueNotWorse"], retbins=True, q=20,duplicates='drop')
train["qcut_90"], updown = pd.qcut(train["NumberOfTimes90DaysLate"], retbins=True, q=20,duplicates='drop')

fig = plt.figure(figsize=(18,4))
ax1 = fig.add_subplot(131)
(train.groupby('qcut_30-59')['SeriousDlqin2yrs'].sum()/train.groupby('qcut_30-59')['SeriousDlqin2yrs'].count()).plot()
ax2 = fig.add_subplot(132)
(train.groupby('qcut_60-89')['SeriousDlqin2yrs'].sum()/train.groupby('qcut_60-89')['SeriousDlqin2yrs'].count()).plot()
ax3 = fig.add_subplot(133)
(train.groupby('qcut_90')['SeriousDlqin2yrs'].sum()/train.groupby('qcut_90')['SeriousDlqin2yrs'].count()).plot()
plt.show()

• 逾期的次数越多，客户违约率就越高，符合正常逻辑。

负债率

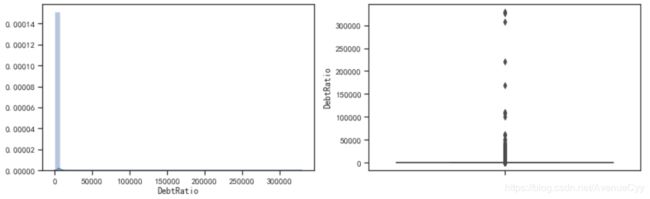
fig= plt.figure(figsize=(14,4))
ax1=fig.add_subplot(1,2,1)
sns.distplot(train['DebtRatio'],kde=True)
ax1=fig.add_subplot(1,2,2)
sns.boxplot(y=train['DebtRatio'])
plt.show()

• 负债率主要集中在“0附近”，正常来说，负债率应该是小于1的。但却有很多的值大于1，甚至上万，即存在异常值。

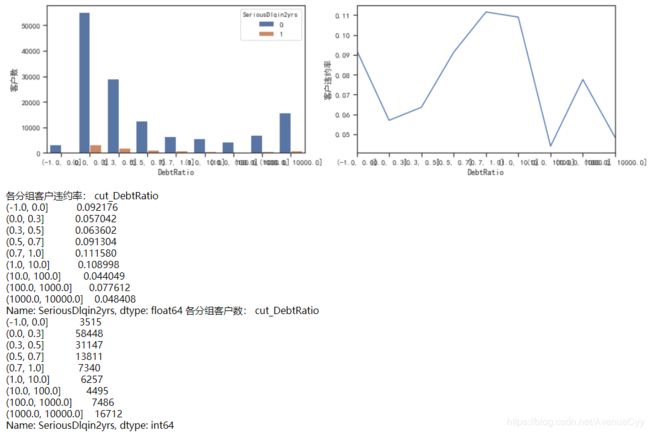
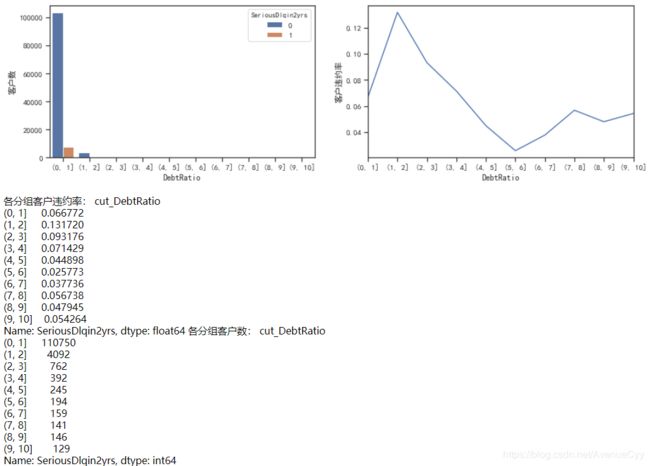
cut_num=[-1,0,0.3,0.5,0.7,1,10,100,1000,10000]
get_compare_plot(train,feature_plot="DebtRatio",cut_num=cut_num,is_qcut=False)

• 负债率在0-1之间，随着负债率的增加，违约率也在增加。
• 当负债率为0时，有着较高的违约率，这点需要从业务上去理解。可能是因为若无负债（每月偿还债务，赡养费，生活费用除以月总收入），比较不靠谱。
• 当负债率大于1时，随着负债率的增加，违约率无显著的变化规律。这里对大于1继续进行分析。

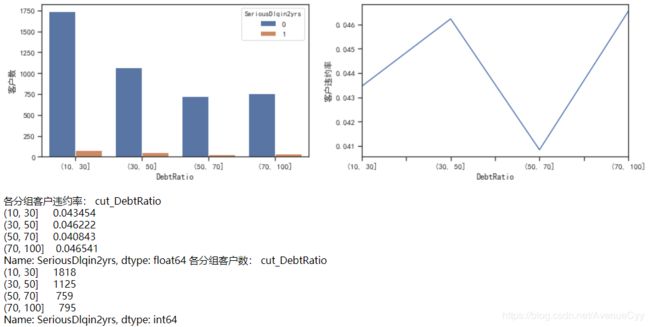
cut_num=[10,30,50,70,100]
get_compare_plot(train,feature_plot="DebtRatio",cut_num=cut_num,is_qcut=False)

• 负债率在10-100之间时，没有逻辑规律，虽然从图像上看数据变化较大，但违约率都在0.04左右，很低。

cut_num=[]
for i in np.arange(0,11,1):
    cut_num.append(i)
get_compare_plot(train,feature_plot="DebtRatio",cut_num=cut_num,is_qcut=False)

• 负债率在0-2时，随着负债率的增加，违约率也在增加。但大于2之后，负债率下降，然后在0.03-0.05上下波动。
• 可认定2为阈值，大于2的为异常值。但这个异常值的处理却有些问题，跟月薪的关系很大。

月薪

a=(len(train)-len(train_nM))/len(train)*100
print('家属人数缺失值比例为%.2f%%'%(a))
家属人数缺失值比例为19.82%。

• 之前说过，月薪存在缺失值，这里可看到缺失值的比例为19.82%。数值很大，采用随机森林进行填充。

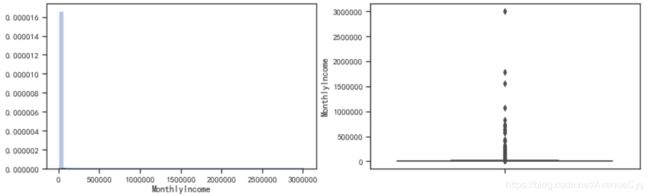
fig= plt.figure(figsize=(14,4))
ax1=fig.add_subplot(1,2,1)
sns.distplot(train_nM['MonthlyIncome'],kde=True)
ax1=fig.add_subplot(1,2,2)
sns.boxplot(y=train_nM['MonthlyIncome'])
plt.show()

• 月薪的分布也是极度右偏的。有数额特别大的异常值。

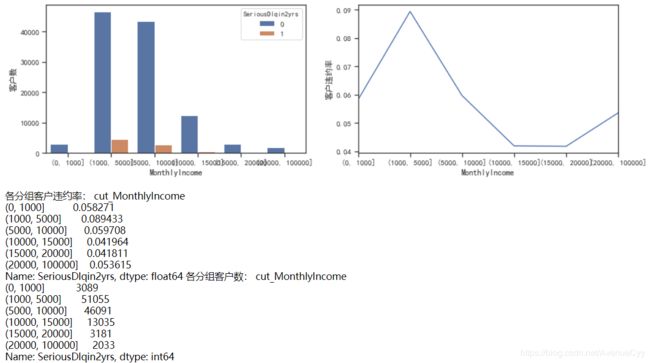
cut_num=[0,1000,5000,10000,15000,20000,100000]
get_compare_plot(train,feature_plot="MonthlyIncome",cut_num=cut_num,is_qcut=False)

• 随着月薪的增加，客户违约率逐渐下降。当月薪超过20000后，违约率又有上升趋势，说明月薪太大，客户收入不稳定。
• 注意到0-1000这个月薪范围内跟正常的规律不一样。进行进一步的判断。

train_nM_2=train_nM.loc[(train_nM['MonthlyIncome']>1)&(train_nM['MonthlyIncome']<=3000),:]
sns.scatterplot(x='MonthlyIncome',y='DebtRatio',data=train_nM_2,hue='SeriousDlqin2yrs')

• 绘制月薪和负债率的散点图，发现500-3000月薪的负债率都很低，有比较稳定的规律性，但是0-500之间却很高。因此对0-500进行进一步分析。

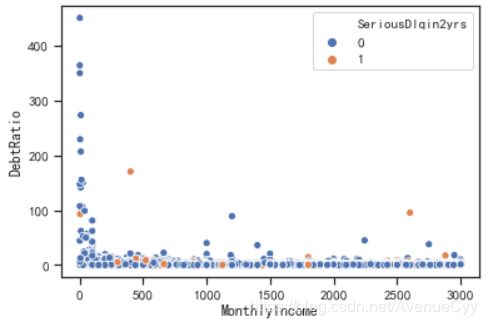
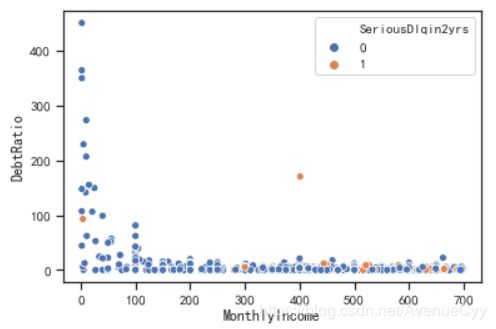
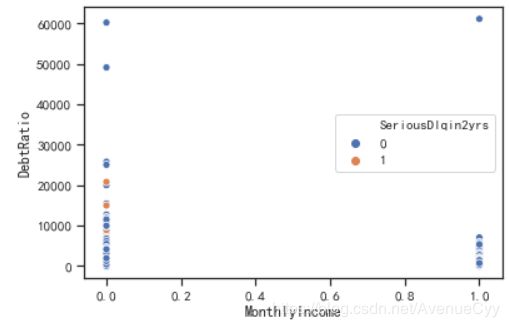
train_nM_2=train_nM.loc[(train_nM['MonthlyIncome']>1)&(train_nM['MonthlyIncome']<700),:]
sns.scatterplot(x='MonthlyIncome',y='DebtRatio',data=train_nM_2,hue='SeriousDlqin2yrs')

• 月薪在0-100之间，负债率特别高，但是违约率却很低，说明月薪在这里被算小了，可能是客户在输入金额时把自己的年薪输入进去，由于输入金额时，差的都是1000倍。因此，将0-100之间的金额乘1000再除以12，以求出正常的月薪，同时负债率也要跟着一起变化0.012倍。

注：
另外，通过分析还发现了月薪为0,1和NaN值的，负债率也特别高。这里不把1当做金额输入错误的值是因为月薪为1的有605个，因此怀疑其跟0和NaN的含义一样，都是“空值”。
之前有过想法是这些负债率在计算的时候，由于月薪未知，所以计算出来的负债率其实是每个月需要偿还的钱。但这个想法也只是个假设，具体的问题还要跟业务相关联。所以，不对这些月薪进行这个假设处理，而是进行分箱处理。

开放式贷款和信贷数量

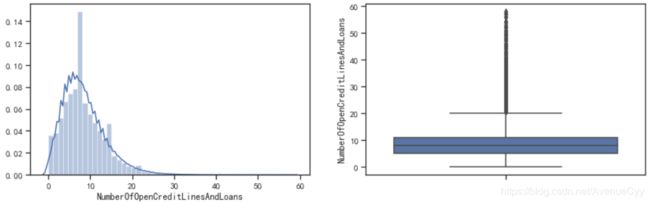
fig= plt.figure(figsize=(14,4))
ax1=fig.add_subplot(1,2,1)
sns.distplot(train['NumberOfOpenCreditLinesAndLoans'],kde=True)
ax1=fig.add_subplot(1,2,2)
sns.boxplot(y=train['NumberOfOpenCreditLinesAndLoans'])
plt.show()

• 通过直方图可以看到，数据是右偏分布，可能存在异常值。
• 通过箱线图可以看到，存在一些离散值。但由于这些离散值较多且连续，因此需要进一步判断是不是异常值。

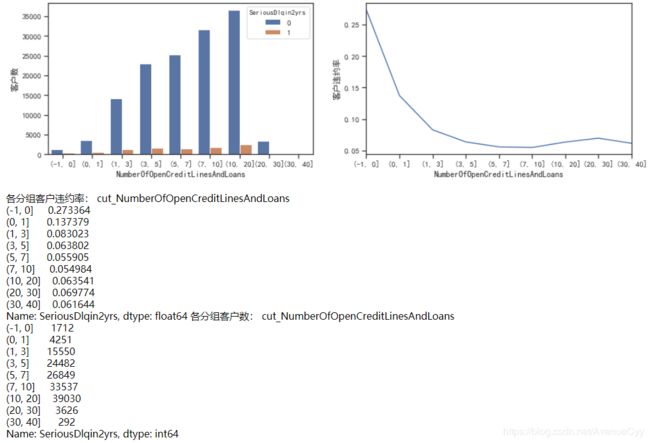
cut_num=[-1,0,1,3,5,7,10,20,30,40]
get_compare_plot(train,feature_plot="NumberOfOpenCreditLinesAndLoans",cut_num=cut_num,is_qcut=False)

• 随着信贷数量增加，客户违约率在不断降低，最后基本保持在0.06左右。即信贷数量越多，说明该客户越值得信赖。
• 这里可以认定大于30的为异常值，因为30-40的样本量突然下降。
• 但也可以通过箱线图看出，30-40的值为连续的，没有断点。这里先不按照异常值进行处理。

抵押贷款和房地产贷款数量

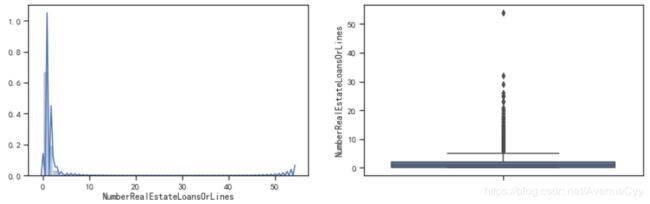
fig= plt.figure(figsize=(14,4))
ax1=fig.add_subplot(1,2,1)
sns.distplot(train['NumberRealEstateLoansOrLines'],kde=True)
ax1=fig.add_subplot(1,2,2)
sns.boxplot(y=train['NumberRealEstateLoansOrLines'])
plt.show()

• 通过直方图能看到数据是极度右偏的分布，另外箱线图上也能明显地看到离群点。

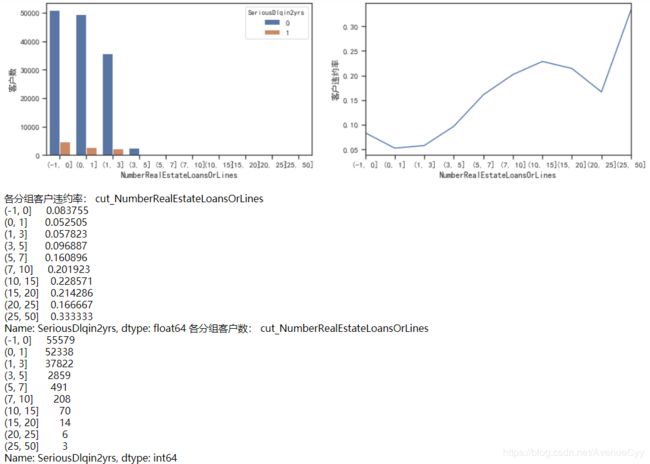
cut_num=[-1,0,1,3,5,7,10,15,20,25,50]
get_compare_plot(train,feature_plot="NumberRealEstateLoansOrLines",cut_num=cut_num,is_qcut=False)

• 当抵押贷款和房地产贷款数量为0时，客户有一定的违约率，跟之前的负债率一样。
• 当抵押贷款和房地产贷款数量大于0，小于20时，随着数量的增加，客户违约率也在不断增加。
• 由于10-20内有84个样本，大于20的一共有9个样本。因此，从样本数量和违约规律上，可以认定大于20的为异常，将其删除。

家属人数（配偶，子女等）

b=(len(train)-len(train_nN))/len(train)*100
print('家属人数缺失值比例为%.2f%%'%(b))
家属人数缺失值比例为2.62%

• 之前说过，家属人数存在缺失值，这里可看到缺失值的比例为2.62%。数值不大，可以使用众数填充。

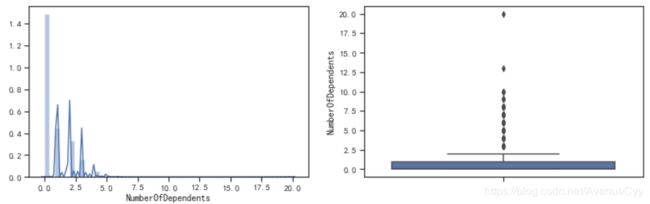
fig= plt.figure(figsize=(14,4))
ax1=fig.add_subplot(1,2,1)
sns.distplot(train_nN['NumberOfDependents'],kde=True)
ax1=fig.add_subplot(1,2,2)
sns.boxplot(y=train_nN['NumberOfDependents'])
plt.show()

• 从箱线图可以很明显地看到存在异常值。那个20特别醒目。。。

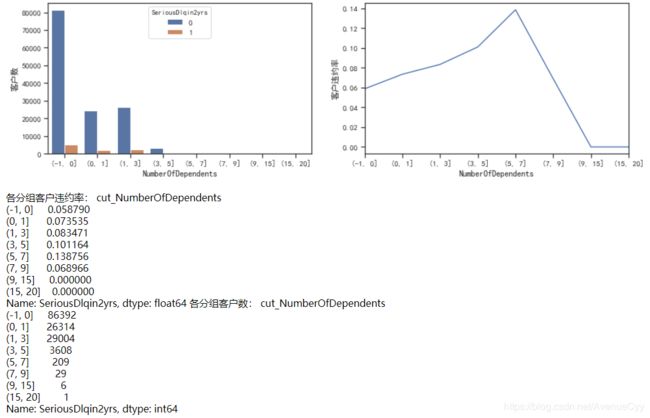
cut_num=[-1,0,1,3,5,7,9,15,20]
get_compare_plot(train,feature_plot="NumberOfDependents",cut_num=cut_num,is_qcut=False)

• 随着家属人数增加，客户违约率增加。因为家属人数增加，家庭开销增加，需要的开销也就增加。当单身时（家属人数为0）客户违约率最小为0.058。
• 异常值20需删除。
• 将大于5的可分为一箱处理。

3.数据预处理

数据预处理，这里包含一些之前整理过的异常值处理，填补缺失值和数据不平衡处理的方法。

去除重复值

train.duplicated(keep='first').sum()
609
train.drop_duplicates(keep='first',inplace=True)
train.duplicated(keep='first').sum()
0
train.index = range(train.shape[0])

异常值处理

def data_deal(data):
    #data=data[data['RevolvingUtilizationOfUnsecuredLines']<=2]
    data=data[(data['age']>=18)&(data['age']<=100)]
    data=data[data['NumberOfTime30-59DaysPastDueNotWorse']<24]
    data=data[data['NumberOfTime60-89DaysPastDueNotWorse']<12]
    data=data[data['NumberOfTimes90DaysLate']<8]
    data=data[data['DebtRatio']<=1]
    #data=data[data['NumberOfOpenCreditLinesAndLoans']<50]
    data=data[data['NumberRealEstateLoansOrLines']<20]
    data=data[data['NumberOfDependents']<20]
    return data
    
train_data = data_deal(train)
test_data = data_deal(test)

填补缺失值

众数填补缺失值

train_data.loc[:,"NumberOfDependents"] = train_data.loc[:,"NumberOfDependents"].fillna(train_data.loc[:,"NumberOfDependents"].median())

随机森林填补缺失值

def fill_missing_rf(X,y,to_fill):

    df = X.copy()
    fill = df.loc[:,to_fill]
    df = pd.concat([df.loc[:,df.columns != to_fill],pd.DataFrame(y)],axis=1)

    Ytrain = fill[fill.notnull()]
    Ytest = fill[fill.isnull()]

    Xtrain = df.loc[Ytrain.index,:]
    Xtest = df.loc[Ytest.index,:]
    
    rfr = rfr(n_estimators=200)
    rfr = rfr.fit(Xtrain,Ytrain)
    Ypredict = rfr.predict(Xtest)
    
    return Ypredict

X = train_data.iloc[:,1:]
y = train_data["SeriousDlqin2yrs"]

y_pred = fill_missing_rf(X,y,"MonthlyIncome")
train_data.loc[train_data.loc[:,"MonthlyIncome"].isnull(),"MonthlyIncome"] = y_pred

数据不平衡处理

之前提到过数据中正负样本比例不均衡，为了尽可能捕捉坏样本。这里采用SMOTE算法对数据进行上采样。

X = train_data.iloc[:,1:]
y = train_data.iloc[:,0]
 
n_sample = X.shape[0]
n_1_sample = y.value_counts()[1]
n_0_sample = y.value_counts()[0]
print('样本个数：{}; 坏样本(1)占{:.2%}; 好样本(0)占{:.2%}'.format(n_sample,n_1_sample/n_sample,n_0_sample/n_sample))
样本个数：149101; 坏样本(1)占6.59%; 好样本(0)占93.41%

sm = SMOTE(random_state=42)
X,y = sm.fit_sample(X,y)

n_sample_ = X.shape[0]
n_1_sample = pd.Series(y).value_counts()[1]
n_0_sample = pd.Series(y).value_counts()[0]
 
print('样本个数：{}; 坏样本(1)占{:.2%}; 好样本(0)占{:.2%}'.format(n_sample_,n_1_sample/n_sample_,n_0_sample/n_sample_))
样本个数：278540; 坏样本(1)占50.00%; 好样本(0)占50.00%

小结

通过对数据进行探索性分析，更加了解数据，从中观察出数据的一些规律和问题，这样在后续的预处理过程中，也能有些思路。

以上是对数据分析和处理的过程，但其中还有很多的不足，比如对月薪和负债率的分析处理，数据预处理的方式等，大家有好的建议可以多多指正，感谢！

接下来是对数据进行特征工程，如特征衍生，数据分箱等。构建逻辑回归模型来进行预测，并利用ROC-AUC和KS进行评估。最后建立评分卡。

数据挖掘项目：银行信用评分卡建模分析（下篇）