数据挖掘项目:银行信用评分卡建模分析(下篇)
以下是银行信用评分卡建模分析下篇的内容,包括特征工程,构建模型,模型评估,评分卡建立这四部分。其中如果有一些地方分析的不正确,希望大家多多指正,感谢!
上篇文章的链接:数据挖掘项目:银行信用评分卡建模分析(上篇)
4.特征工程
特征处理和特征生成
特征衍生
构建三个新的特征:总违约数,违约计数和每个月的支出。
def get_more_features(data):
data['AllNumlate']=data['NumberOfTime30-59DaysPastDueNotWorse']+data['NumberOfTime60-89DaysPastDueNotWorse']+data['NumberOfTimes90DaysLate']
data['Monthlypayment']=data['DebtRatio']*data['MonthlyIncome']
return data
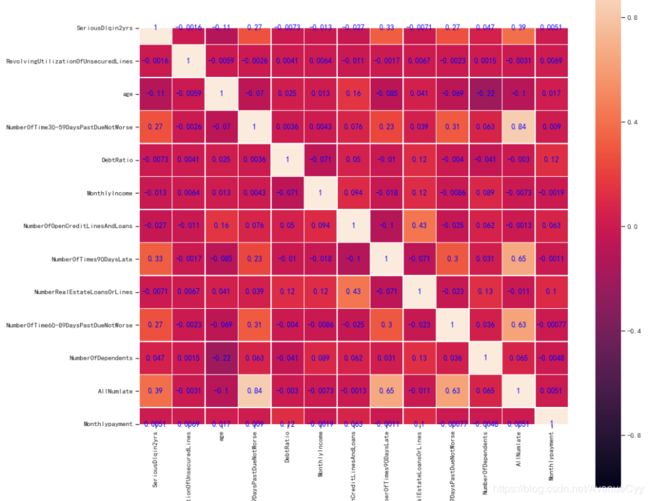
特征相关性
correlation_table = pd.DataFrame(train_data.corr())
fig = plt.figure(figsize=(15,15))
ax1 = fig.add_subplot(1,1,1)
sns.heatmap(correlation_table,annot=True,ax=ax1,square = True, vmax=1.0,vmin=-1.0,linewidths=.5,annot_kws={'size': 12, 'weight': 'bold', 'color': 'blue'})
- 总违约数和30-59天的违约数之间有很大的相关性,0.84。因为30-59天的违约数相比于60-89和90天以上的次数过多。但这个还是选择保留该特征,一是因为有比较重要的实际意义。
划分测试集和训练集
from sklearn.model_selection import train_test_split
X = pd.DataFrame(X)
y = pd.DataFrame(y)
X_train, X_vali, Y_train, Y_vali = train_test_split(X,y,test_size=0.3,random_state=0)
# 训练集
model_data = pd.concat([Y_train, X_train], axis=1)
model_data.index = range(model_data.shape[0])
model_data.columns = train_data.columns
#验证集
vali_data = pd.concat([Y_vali, X_vali], axis=1)
vali_data.index = range(vali_data.shape[0])
vali_data.columns = train_data.columns
数据分箱
关于WOE和IV值的概念在数据分箱、WOE、IV的意义中有比较详细的描述。
这里让WOE的值单调是为了让woe(x)与y之间具备线性的关系,更有助于人们的理解。
数据分箱的大体思路如下:
- 等频分箱。由于不同的数据分组不一样,因此不采用等距分箱。这里等频分箱的分箱数一定要选的足够大20-40之间,因为有的样本占比太大,分箱数少的话,没有区分性。
- 确保每个箱内都有正负样本。由于要计算WOE和IV值,从公式上可以看出,要计算这两个值,需要每个分组内都包含正负样本。
- 卡方分箱。卡方可以检验两类别的相似性。可对等频分箱后的结果,进行更为精确的分箱。但这里并不采用卡方检验的p值决定最终的分箱。
- 根据WOE和IV值确定最佳分箱数。这里WOE要满足单调性,IV值要在一定的范围内,过大过小都说明该特征有问题。

以下为代码部分。
def graphforbestbin(DF, X, Y, n=5,q=20,graph=True):
global bins_df
DF = DF[[X,Y]].copy()
# 等频分箱
DF["qcut"],bins = pd.qcut(DF[X], retbins=True, q=q,duplicates="drop")
coount_y0 = DF.loc[DF[Y]==0].groupby(by="qcut").count()[Y]
coount_y1 = DF.loc[DF[Y]==1].groupby(by="qcut").count()[Y]
num_bins = [*zip(bins,bins[1:],coount_y0,coount_y1)]
# 判断分箱后每个箱内是否都有好坏样本,没有的进行合并
for i in range(q):
if 0 in num_bins[0][2:]:
num_bins[0:2] = [(
num_bins[0][0],
num_bins[1][1],
num_bins[0][2]+num_bins[1][2],
num_bins[0][3]+num_bins[1][3])]
continue
for i in range(len(num_bins)):
if 0 in num_bins[i][2:]:
num_bins[i-1:i+1] = [(
num_bins[i-1][0],
num_bins[i][1],
num_bins[i-1][2]+num_bins[i][2],
num_bins[i-1][3]+num_bins[i][3])]
break
else:
break
# 计算WOE值
def get_woe(num_bins):
columns = ["min","max","count_0","count_1"]
df = pd.DataFrame(num_bins,columns=columns)
df["total"] = df.count_0 + df.count_1
df["percentage"] = df.total / df.total.sum()
df["bad_rate"] = df.count_1 / df.total
df["good%"] = df.count_0/df.count_0.sum()
df["bad%"] = df.count_1/df.count_1.sum()
df["woe"] = np.log(df["good%"] / df["bad%"])
return df
# 计算IV值
def get_iv(df):
rate = df["good%"] - df["bad%"]
iv = np.sum(rate * df.woe)
return iv
# 利用卡方检验进行分箱,将两类相近的样本进行合并
# 合并方式为按照大小顺序改变上下限
IV = []
axisx = []
while len(num_bins) > n:
pvs = []
for i in range(len(num_bins)-1):
x1 = num_bins[i][2:]
x2 = num_bins[i+1][2:]
pv = scipy.stats.chi2_contingency([x1,x2])[1]
pvs.append(pv)
i = pvs.index(max(pvs))
num_bins[i:i+2] = [(
num_bins[i][0],
num_bins[i+1][1],
num_bins[i][2]+num_bins[i+1][2],
num_bins[i][3]+num_bins[i+1][3])]
bins_df = pd.DataFrame(get_woe(num_bins))
axisx.append(len(num_bins))
IV.append(get_iv(bins_df))
# 具体分多少箱,不看卡方值和p值,根据IV值来进行判断
# 绘制出不同分箱效果下的IV值,选取最佳的分箱策略
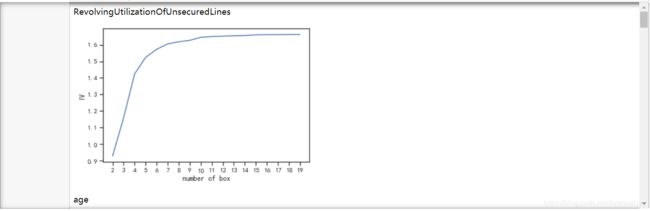
if graph:
plt.figure()
plt.plot(axisx,IV)
plt.xticks(axisx)
plt.xlabel("number of box")
plt.ylabel("IV")
plt.show()
return bins_df
for i in train.columns[1:]:
print(i)
graphforbestbin(model_data,i,"SeriousDlqin2yrs",n=2,q=20)
- 寻找随着分箱数的增加,IV增加的拐点,以确定分箱个数。
- 对于本身不是连续型的变量需要手动分箱,而连续变量可以采用以上方法进行自动分箱。
- 观察大致分箱结果的IV值,可以发现哪些特征是有用的,哪些是无用的,进行特征选择。
自动分箱和非自动分箱
对连续型数据采用自动分箱。
#能自动分箱的变量
auto_col_bins = {"RevolvingUtilizationOfUnsecuredLines":6,
"age":5,
"DebtRatio":4,
"MonthlyIncome":3,
"NumberOfOpenCreditLinesAndLoans":4}
#不能使用自动分箱的变量
hand_bins = {"NumberOfTime30-59DaysPastDueNotWorse":[0,1,2,13]
,"NumberOfTimes90DaysLate":[0,1,2,17]
,"NumberRealEstateLoansOrLines":[0,1,2,4,54]
,"NumberOfTime60-89DaysPastDueNotWorse":[0,1,2,8]
,"NumberOfDependents":[0,1,2,3]}
#保证区间覆盖使用 np.inf替换最大值,用-np.inf替换最小值。使分箱的拟合性更强。
hand_bins = {k:[-np.inf,*v[:-1],np.inf] for k,v in hand_bins.items()}
bins_of_col = {}
# 生成自动分箱的分箱区间和分箱后的 IV 值
for col in auto_col_bins:
bins_df = graphforbestbin(model_data,col
,"SeriousDlqin2yrs"
,n=auto_col_bins[col]
,q=20
,graph=False)
bins_list = sorted(set(bins_df["min"]).union(bins_df["max"]))
#保证区间覆盖使用 np.inf 替换最大值 -np.inf 替换最小值
bins_list[0],bins_list[-1] = -np.inf,np.inf
bins_of_col[col] = bins_list
#合并手动分箱数据
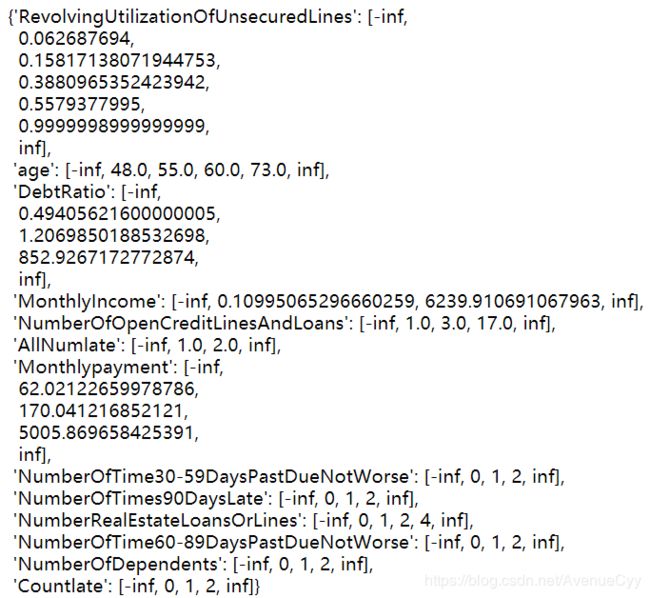
bins_of_col.update(hand_bins)
bins_of_col
分箱后的WOE值
def get_woe(df,col,y,bins):
df = df[[col,y]].copy()
df["cut"] = pd.cut(df[col],bins)
bins_df = df.groupby("cut")[y].value_counts().unstack()
woe = bins_df["woe"] = np.log((bins_df[0]/bins_df[0].sum())/(bins_df[1]/bins_df[1].sum()))
return woe
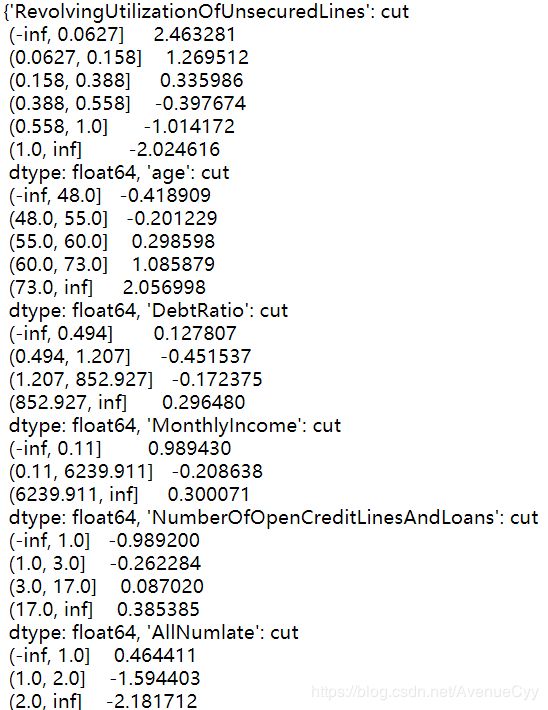
woeall = {}
for col in bins_of_col:
woeall[col] = get_woe(model_data,col,"SeriousDlqin2yrs",bins_of_col[col])
woeall
- 发现DebtRatio,NumberOfOpenCreditLinesAndLoans,NumberRealEstateLoansOrLines这些特征的IV值很低。根据之前探索性数据分析的结果进行人为重新分箱。
- 对于WOE值不是单调变化的,需要重新人为进行调整。
- 若调整后的WOE和IV值仍然不满足要求,则将该特征删除。
#能自动分箱的变量
auto_col_bins = {"RevolvingUtilizationOfUnsecuredLines":6,
"age":6,
# "DebtRatio":5,
"MonthlyIncome":5,
# "NumberOfOpenCreditLinesAndLoans":4,
"Monthlypayment":6}
#不能使用自动分箱的变量
hand_bins = {"NumberOfTime30-59DaysPastDueNotWorse":[0,1,2,13]
,"NumberOfTimes90DaysLate":[0,1,2,17]
,"NumberRealEstateLoansOrLines":[0,1,2,4,54]
,"NumberOfTime60-89DaysPastDueNotWorse":[0,1,2,8]
,"NumberOfDependents":[0,1,2,3,5]
,"DebtRatio":[0,0.3,0.5,1,1.5,2]
,"NumberRealEstateLoansOrLines":[0,1,3,5]
,"NumberOfOpenCreditLinesAndLoans":[0,1,3,5,7]
,"AllNumlate":[0,1]
,"Countlate":[0,1,2,3]}
#保证区间覆盖使用 np.inf替换最大值,用-np.inf替换最小值
hand_bins = {k:[-np.inf,*v[:-1],np.inf] for k,v in hand_bins.items()}
这里对以上不合格的特征进行手动的人为分箱。
WOE替换分箱结果
model_woe = pd.DataFrame(index=model_data.index)
for col in bins_of_col:
model_woe[col] = pd.cut(model_data[col],bins_of_col[col]).map(woeall[col])
model_woe["SeriousDlqin2yrs"] = model_data["SeriousDlqin2yrs"]
对测试集采用同样的方法进行替换
vali_woe = pd.DataFrame(index=vali_data.index)
for col in bins_of_col:
vali_woe[col] = pd.cut(vali_data[col],bins_of_col[col]).map(woeall[col])
vali_woe["SeriousDlqin2yrs"] = vali_data["SeriousDlqin2yrs"]
vali_X = vali_woe.iloc[:,:-1]
vali_y = vali_woe.iloc[:,-1]
5.构建模型
X = model_woe.iloc[:,:-1]
y = model_woe.iloc[:,-1]
建立逻辑回归模型
逻辑回归算法说明
lr = LR().fit(X,y)
lr.score(vali_X,vali_y)
0.8011675781970135
- 最初没有对分箱探索时的结果是0.786。
调整模型参数
这里主要调整sklearn中逻辑回归的两个参数,惩罚系数C和最大迭代次数max_iter。
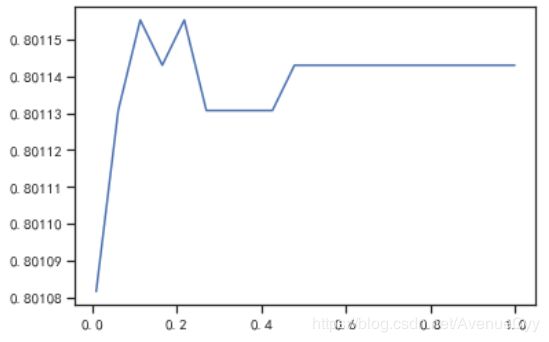
c_1 = np.linspace(0.01,1,20)
score = []
for i in c_1:
lr = LR(solver='liblinear',C=i).fit(X,y)
score.append(lr.score(vali_X,vali_y))
plt.figure()
plt.plot(c_1,score)
plt.show()
- 通过不断调整C的大小,找到使score最高的参数。最终得到的C为0.08
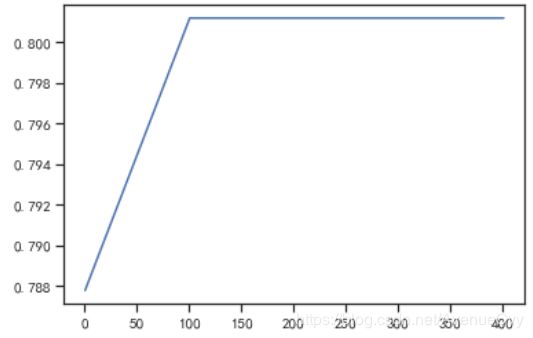
score = []
for i in np.arange(1,500,100):
lr = LR(solver='liblinear',C=0.025,max_iter=i).fit(X,y)
score.append(lr.score(vali_X,vali_y))
plt.figure()
plt.plot([1,2,3,4,5,6],score)
plt.show()
- 最优的迭代次数定为150。
最终将调整的参数带入模型后,发现模型的准确率并没有什么变化。说明初始的参数即为最优的参数。
6.模型评估
模型评估指标说明
ROC-AUC曲线
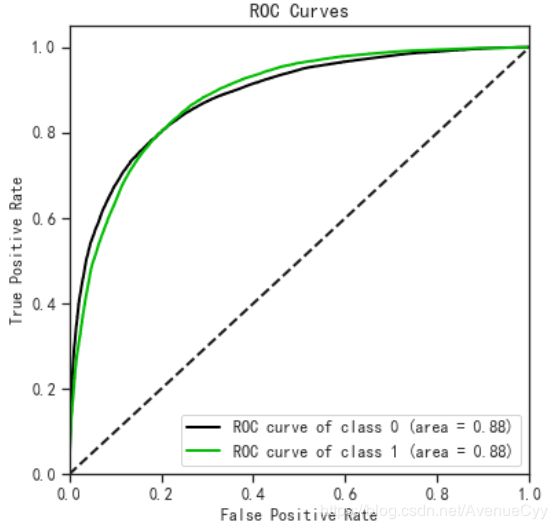
绘制ROC曲线,计算AUC面积,查看模型分类的评估效果。
vali_proba_df = pd.DataFrame(lr.predict_proba(vali_X))
skplt.metrics.plot_roc(vali_y, vali_proba_df,
plot_micro=False,figsize=(6,6),
plot_macro=False)
- AUC面积为0.88,说明模型对正负样本的区分能力还可以。
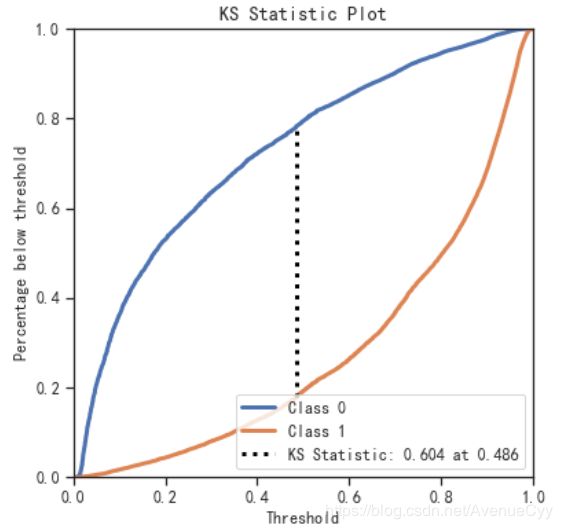
KS值
KS值和AUC值的关系
KS值计算
- KS值为0.604,模型预测性较好。
7.评分卡建立
B = 20/np.log(2)
A = 600 + B*np.log(1/60)
B,A
(28.85390081777927, 481.8621880878296)
- 这里的特定分数和PDO的值都是假定的。
base_score = A - B*lr.intercept_
base_score
array([481.86620974])
- 计算基础分数为481.87。
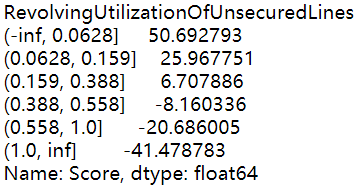
年龄中,每个分箱对应的数值
for i,col in enumerate(X.columns):#[*enumerate(X.columns)]
score = woeall[col] * (-B*lr.coef_[0][i])
score.name = "Score"
score.index.name = col
print(score)
总结
从整个项目来看,最耗时耗力的就是探索性数据分析,在对月薪和负债率的处理上,思考了好久,用尝试了很多的方法,但处理的原因和结果都不太理想,如果大家有好的想法,希望能指点下。
通过评分卡这个项目,了解到了WOE和IV值,虽然对别的模型可能用处不大,但增强了逻辑回归的理解,使其能像线性回归一样具备一定的可解释性。另外,由于数据中有很多的异常值不知道该怎么处理时,也见识到了数据分箱这种方法的强大。
以上就是银行信用评分卡建模分析项目的全部内容,如果对您有所帮助还希望能点赞关注下,感谢大家的阅读!
参考资料
https://www.bilibili.com/video/BV1WJ411k7L3?p=87
https://zhuanlan.zhihu.com/p/50051580
https://blog.csdn.net/gxhzoe/article/details/80428560
https://cloud.tencent.com/developer/article/1092198?from=10680