算法笔试题:(Python实现)------ 初级算法
算法笔试题:(Python实现)------ 初级算法
- 初级算法
- 数组
- Python实现
- 从排序数组中删除重复项
- 买卖股票的最佳时机 II
- 旋转数组
- 存在重复
- 只出现一次的数字
- 两个数组的交集 II
- 加一
- 移动零
- 两数之和
- 有效的数独
- 旋转图像
- 字符串
- Python实现
- 反转字符转
- 整数反转
- 字符串中的第一个唯一字符
- 有效的字母异位词
- 验证回文字符串
- 字符串转换整数 (atoi)
- 实现 strStr()
- 最长公共前缀
- 外观数列
- 链表
- 删除链表中的节点
- 删除链表的倒数第N个节点
- 反转链表
- 合并两个有序链表
- 回文链表
- 环形链表
- 树
- Python实现
- 二叉树的最大深度
- 验证二叉搜索树
- 对称二叉树
- 二叉树的层次遍历
- 将有序数组转换为二叉搜索树
- 排序和搜索
- Python实现
- 合并两个有序数组
- 第一个错误的版本
- 动态规划
- Python实现
- 爬楼梯
- 买卖股票的最佳时机
- 最大子序和
- 打家劫舍
- 设计问题
- Python实现
- Shuffle an Array
- 最小栈
- 数学
- Python实现
- Fizz Buzz
- 计数质数
- 3的幂
- 罗马数字转整数
- 其他
- Python实现
- 位1的个数
- 汉明距离
- 颠倒二进制位
- 缺失数字
- 有效括号
初级算法
数组
Python实现
从排序数组中删除重复项
给定一个排序数组,你需要在原地删除重复出现的元素,使得每个元素只出现一次,返回移除后数组的新长度。
不要使用额外的数组空间,你必须在原地修改输入数组并在使用 O(1) 额外空间的条件下完成。
示例 1:
给定数组 nums = [1,1,2],
函数应该返回新的长度 2, 并且原数组 nums 的前两个元素被修改为 1, 2。
你不需要考虑数组中超出新长度后面的元素。
示例 2:
给定 nums = [0,0,1,1,1,2,2,3,3,4],
函数应该返回新的长度 5, 并且原数组 nums 的前五个元素被修改为 0, 1, 2, 3, 4。
你不需要考虑数组中超出新长度后面的元素。
说明:
为什么返回数值是整数,但输出的答案是数组呢?
请注意,输入数组是以“引用”方式传递的,这意味着在函数里修改输入数组对于调用者是可见的。
方法一:
class Solution(object):
def removeDuplicates(self,nums):
return len(set(nums))
方法二:
class Solution2(object):
def removeDuplicates(self,nums):
i = 0
while i < len(nums)-1:
if nums[i] == nums[i+1]:
nums.remove(nums[i])
else:
i =i+1
return len(nums)
买卖股票的最佳时机 II
给定一个数组,它的第 i 个元素是一支给定股票第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易(多次买卖一支股票)。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
输入: [7,1,5,3,6,4]
输出: 7
解释: 在第 2 天(股票价格 = 1)的时候买入,在第 3 天(股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
随后,在第 4 天(股票价格 = 3)的时候买入,在第 5 天(股票价格 = 6)的时候卖出, 这笔交易所能获得利润 = 6-3 = 3 。
示例 2:
输入: [1,2,3,4,5]
输出: 4
解释: 在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
注意你不能在第 1 天和第 2 天接连购买股票,之后再将它们卖出。
因为这样属于同时参与了多笔交易,你必须在再次购买前出售掉之前的股票。
示例 3:
输入: [7,6,4,3,1]
输出: 0
解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。
class Solution(object):
def maxProfit(self, prices):
"""
:type prices: List[int]
:rtype: int
"""
sell = 0
buy = 0
Profit = 0
length = len(prices)
tag = 0
if length <=1:
return 0
else:
for i in range(length-1):
if tag == 0 and prices[i] < prices[i+1]:
buy = prices[i]
tag =1
elif tag == 1 and prices[i] > prices[i+1]:
sell = prices[i]
Profit += (sell-buy)
tag=0
if tag == 0 and sell == 0:
result = 0
# 用来解决[1,2,3,4,5]这种一直没有卖出的情况
elif tag == 1:
Profit += prices[length - 1] - buy
return Profit
旋转数组
**给定一个数组,将数组中的元素向右移动 k 个位置,其中 k 是非负数。
示例 1:
输入: [1,2,3,4,5,6,7] 和 k = 3
输出: [5,6,7,1,2,3,4]
解释:
向右旋转 1 步: [7,1,2,3,4,5,6]
向右旋转 2 步: [6,7,1,2,3,4,5]
向右旋转 3 步: [5,6,7,1,2,3,4]
示例 2:
输入: [-1,-100,3,99] 和 k = 2
输出: [3,99,-1,-100]
解释:
向右旋转 1 步: [99,-1,-100,3]
向右旋转 2 步: [3,99,-1,-100]
说明:
尽可能想出更多的解决方案,至少有三种不同的方法可以解决这个问题。
要求使用空间复杂度为 O(1) 的 原地 算法。**
class Solution(object):
def rotate(self, nums, k):
"""
:type nums: List[int]
:type k: int
:rtype: None Do not return anything, modify nums in-place instead.
"""
l = len(nums)
k = k%l
nums[:] = nums[l-k:]+nums[:l-k]
return nums
存在重复
给定一个整数数组,判断是否存在重复元素。
如果任何值在数组中出现至少两次,函数返回 true。如果数组中每个元素都不相同,则返回 false。
示例 1:
输入: [1,2,3,1]
输出: true
示例 2:
输入: [1,2,3,4]
输出: false
示例 3:
输入: [1,1,1,3,3,4,3,2,4,2]
输出: true
class Solution(object):
def containsDuplicate(self,nums):
num_dict = {}
for i in nums:
if i not in num_dict:
num_dict[i] = 0
else:
return True
return False
l利用Python 的Set
class Solution(object):
def containsDuplicate(self,nums):
if len(set(nums)) < len(nums):
return True
else:
return False
只出现一次的数字
给定一个非空整数数组,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。
说明:
你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实现吗?
示例 1:
输入: [2,2,1]
输出: 1
示例 2:
输入: [4,1,2,1,2]
输出: 4
一个技巧:
class Solution(object):
def singleNumber(self,nums):
res = 0
for i in nums:
res ^= i
return res
class Solution(object):
def singleNumber(self,nums):
num_dict = {}
for i in nums:
if i not in num_dict:
num_dict[i] = 1
else:
num_dict[i] += 1
for i in num_dict.keys():
if num_dict[i] == 1:
return i
两个数组的交集 II
给定两个数组,编写一个函数来计算它们的交集。
示例 1:
输入: nums1 = [1,2,2,1], nums2 = [2,2]
输出: [2,2]
示例 2:
输入: nums1 = [4,9,5], nums2 = [9,4,9,8,4]
输出: [4,9]
说明:
输出结果中每个元素出现的次数,应与元素在两个数组中出现的次数一致。
我们可以不考虑输出结果的顺序。
进阶:
如果给定的数组已经排好序呢?你将如何优化你的算法?
如果 nums1 的大小比 nums2 小很多,哪种方法更优?
如果 nums2 的元素存储在磁盘上,磁盘内存是有限的,并且你不能一次加载所有的元素到内存中,你该怎么办?
class Solution(object):
def intersect(self,nums1,nums2):
nums1 = sorted(nums1)
nums2 =sorted(nums2)
new_list=[]
i,j = 0,0
while i < len(nums1) and j <len(nums2):
if nums1[i] == nums2[j]:
new_list.append(nums1[i])
i+=1
j+=1
elif nums1[i] < nums2[j]:
i+=1
else:
j+=1
return new_list
加一
给定一个由整数组成的非空数组所表示的非负整数,在该数的基础上加一。
最高位数字存放在数组的首位, 数组中每个元素只存储单个数字。
你可以假设除了整数 0 之外,这个整数不会以零开头。
示例 1:
输入: [1,2,3]
输出: [1,2,4]
解释: 输入数组表示数字 123。
示例 2:
输入: [4,3,2,1]
输出: [4,3,2,2]
解释: 输入数组表示数字 4321。
class Solution(object):
def plusOne(self, digits):
res = 0
lens = len(digits)
divisor = 1
for i in range(lens):
res += digits[-(i+1)]*divisor
divisor*=10
res += 1
res = [ int(x) for x in str(res)]
return res
移动零
给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。
示例:
输入: [0,1,0,3,12]
输出: [1,3,12,0,0]
说明:
必须在原数组上操作,不能拷贝额外的数组。
尽量减少操作次数。
class Solution(object):
def moveZeroes(self, nums):
"""
:type nums: List[int]
:rtype: None Do not return anything, modify nums in-place instead.
"""
j = 0
for i in range(len(nums)):
if nums[i] != 0:
nums[i],nums[j] = nums[j],nums[i]
j+=1
两数之和
给定一个整数数组 nums 和一个目标值 target,请你在该数组中找出和为目标值的那 两个 整数,并返回他们的数组下标。
你可以假设每种输入只会对应一个答案。但是,你不能重复利用这个数组中同样的元素。
示例:
给定 nums = [2, 7, 11, 15], target = 9
因为 nums[0] + nums[1] = 2 + 7 = 9
所以返回 [0, 1]
class Solution(object):
def twoSum(self,nums,target):
nums_hash = {}
nums_len = len(nums)
for i in range(nums_len):
dif = target -nums[i]
if dif in nums_hash:
return [nums_hash[dif],i]
nums_hash[nums[i]]=i
return []
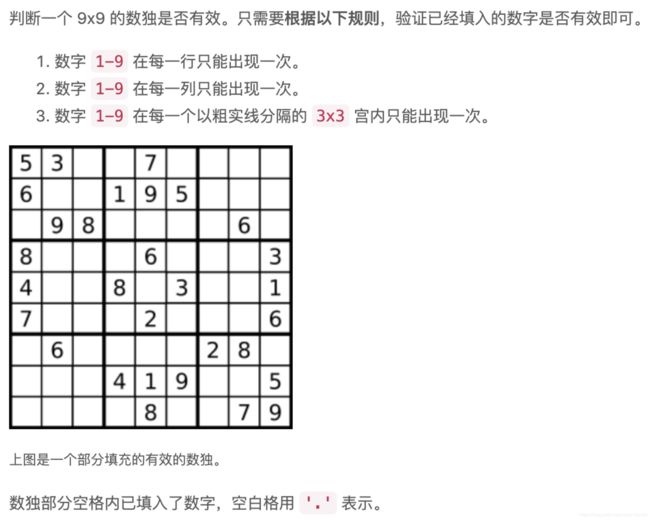
有效的数独
class Solution:
def isValidSudoku(self, board):
"""
:type board: List[List[str]]
:rtype: bool
"""
row = [[] for _ in range(9)]#行
col = [[] for _ in range(9)]#列
area = [[] for _ in range(9)]# 子区域
for i in range(9):
for j in range(9):
element = board[i][j]
if element != '.':#检验是否为数字
top_id = i//3*3 +j//3#子区域的计算
# 如果在这一行列子区域重读出现过了
if element in row[i] or element in col[j] or element in area[top_id]:
return False
else:#未出现就加进去
row[i].append(element)
col[j].append(element)
area[top_id].append(element)
return True
旋转图像
给定一个 n × n 的二维矩阵表示一个图像。
将图像顺时针旋转 90 度。
说明:
你必须在原地旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要使用另一个矩阵来旋转图像。
示例 1:
给定 matrix =
[
[1,2,3],
[4,5,6],
[7,8,9]
],
原地旋转输入矩阵,使其变为:
[
[7,4,1],
[8,5,2],
[9,6,3]
]
示例 2:
给定 matrix =
[
[ 5, 1, 9,11],
[ 2, 4, 8,10],
[13, 3, 6, 7],
[15,14,12,16]
],
原地旋转输入矩阵,使其变为:
[
[15,13, 2, 5],
[14, 3, 4, 1],
[12, 6, 8, 9],
[16, 7,10,11]
]
解法1:
class Solution(object):
def rotate(self, matrix):
"""
:type matrix: List[List[int]]
:rtype: None Do not return anything, modify matrix in-place instead.
"""
length = len(matrix)
for i in range(length):
for j in range(i+1,length):
temp = matrix[i][j]
matrix[i][j] = matrix[j][i]
matrix[j][i] = temp
for i in range(length):#把每一行逆序
matrix[i] = matrix[i][::-1]
解法2:
class Solution:
def rotate(self, matrix):
"""
:type matrix: List[List[int]]
:rtype: void Do not return anything, modify matrix in-place instead.
"""
matrix[:] = list(map(list, zip(*matrix[::-1])))
字符串
Python实现
反转字符转
编写一个函数,其作用是将输入的字符串反转过来。输入字符串以字符数组 char[] 的形式给出。
不要给另外的数组分配额外的空间,你必须原地修改输入数组、使用 O(1) 的额外空间解决这一问题。
你可以假设数组中的所有字符都是 ASCII 码表中的可打印字符。
示例 1:
输入:["h","e","l","l","o"]
输出:["o","l","l","e","h"]
示例 2:
输入:["H","a","n","n","a","h"]
输出:["h","a","n","n","a","H"]
class Solution(object):
def reverseString(self, s):
"""
:type s: List[str]
:rtype: None Do not return anything, modify s in-place instead.
"""
lens = len(s)//2
for i in range(lens):
temp = s[i]
s[i] = s[len(s)-1-i]
s[len(s)-1-i] = temp
整数反转
给出一个 32 位的有符号整数,你需要将这个整数中每位上的数字进行反转。
示例 1:
输入: 123
输出: 321
示例 2:
输入: -123
输出: -321
示例 3:
输入: 120
输出: 21
注意:
假设我们的环境只能存储得下 32 位的有符号整数,则其数值范围为 [−231, 231 − 1]。请根据这个假设,如果反转后整数溢出那么就返回 0。
class Solution(object):
def reverse(self, x):
"""
:type x: int
:rtype: int
"""
if x >= 0:
x = int(str(x)[::-1])
else:
x = -int(str(-x)[::-1])
if x <= 2147483648 and x >= -2147483648:
return x
else:
return 0
字符串中的第一个唯一字符
给定一个字符串,找到它的第一个不重复的字符,并返回它的索引。如果不存在,则返回 -1。
案例:
s = "leetcode"
返回 0.
s = "loveleetcode",
返回 2.
class Solution(object):
def firstUniqChar(self,s):
my_dict = {}
for i in s:
if i in my_dict:
my_dict[i] += 1
else:
my_dict[i] =1
for i in range(len(s)):
if my_dict[s[i]] == 1:
return i
return -1
有效的字母异位词
给定两个字符串 s 和 t ,编写一个函数来判断 t 是否是 s 的字母异位词。
示例 1:
输入: s = "anagram", t = "nagaram"
输出: true
示例 2:
输入: s = "rat", t = "car"
输出: false
说明:
你可以假设字符串只包含小写字母。
进阶:
如果输入字符串包含 unicode 字符怎么办?你能否调整你的解法来应对这种情况?
class Solution(object):
def isAnagram(self, s, t):
"""
:type s: str
:type t: str
:rtype: bool
"""
s = sorted(list(s))
t = sorted(list(t))
if len(s) != len(t):
return False
for i in range(len(s)):
if s[i] != t[i]:
return False
return True
验证回文字符串
给定一个字符串,验证它是否是回文串,只考虑字母和数字字符,可以忽略字母的大小写。
说明:本题中,我们将空字符串定义为有效的回文串。
示例 1:
输入: "A man, a plan, a canal: Panama"
输出: true
示例 2:
输入: "race a car"
输出: false
class Solution(object):
def isPalindrome(self, s):
"""
:type s: str
:rtype: bool
"""
s = list(s.lower())
check = []
for i in s:
if i.isalpha() or i.isdigit():
check.append(i)
lens = len(check)//2
for i in range(lens):
if check[i] != check[len(check)-1-i]:
return False
return True
字符串转换整数 (atoi)
请你来实现一个 atoi 函数,使其能将字符串转换成整数。
首先,该函数会根据需要丢弃无用的开头空格字符,直到寻找到第一个非空格的字符为止。
当我们寻找到的第一个非空字符为正或者负号时,则将该符号与之后面尽可能多的连续数字组合起来,作为该整数的正负号;假如第一个非空字符是数字,则直接将其与之后连续的数字字符组合起来,形成整数。
该字符串除了有效的整数部分之后也可能会存在多余的字符,这些字符可以被忽略,它们对于函数不应该造成影响。
注意:假如该字符串中的第一个非空格字符不是一个有效整数字符、字符串为空或字符串仅包含空白字符时,则你的函数不需要进行转换。
在任何情况下,若函数不能进行有效的转换时,请返回 0。
说明:
假设我们的环境只能存储 32 位大小的有符号整数,那么其数值范围为 [−231, 231 − 1]。如果数值超过这个范围,请返回 INT_MAX (231 − 1) 或 INT_MIN (−231) 。
示例 1:
输入: "42"
输出: 42
示例 2:
输入: " -42"
输出: -42
解释: 第一个非空白字符为 ‘-’, 它是一个负号。
我们尽可能将负号与后面所有连续出现的数字组合起来,最后得到 -42 。
示例 3:
输入: "4193 with words"
输出: 4193
解释: 转换截止于数字 ‘3’ ,因为它的下一个字符不为数字。
示例 4:
输入: "words and 987"
输出: 0
解释: 第一个非空字符是 ‘w’, 但它不是数字或正、负号。
因此无法执行有效的转换。
示例 5:
输入: "-91283472332"
输出: -2147483648
解释: 数字 “-91283472332” 超过 32 位有符号整数范围。
因此返回 INT_MIN (−231) 。
class Solution:
def myAtoi(self, str):
book=0 #标记是否出现过有效字符
sign=0 #标记符号
label=0 #标记符号之前是否出现过有效字符
a=[]
for i in str:
if i==' 'and book==0:
continue
if i=='+':
if label==0:
book=1
label=1
continue
else:
break
if i=='-':
if label==0:
book=1
sign=1
label=1
continue
else:
break
if 47<ord(i)<58:
a.append(i)
book=1
label=1
else:
break
if len(a)==0:
result=0
else:
if sign==0:
result=int(''.join(a)) #''.join(a)把列表变成字符串
else:
result=(-1)*int(''.join(a))
if result>pow(2,31)-1:
return (pow(2,31)-1)
if result<(-1)*pow(2,31):
return (-1)*pow(2,31)
else:
return result
实现 strStr()
实现 strStr() 函数。
给定一个 haystack 字符串和一个 needle 字符串,在 haystack 字符串中找出 needle 字符串出现的第一个位置 (从0开始)。如果不存在,则返回 -1。
示例 1:
输入: haystack = "hello", needle = "ll"
输出: 2
示例 2:
输入: haystack = "aaaaa", needle = "bba"
输出: -1
说明:
当 needle 是空字符串时,我们应当返回什么值呢?这是一个在面试中很好的问题。
对于本题而言,当 needle 是空字符串时我们应当返回 0 。这与C语言的 strstr() 以及 Java的 indexOf() 定义相符。
class Solution:
def strStr(self, haystack, needle):
"""
:type haystack: str
:type needle: str
:rtype: int
"""
i=0
j=0
if needle == "":
return 0
elif needle not in haystack:
return -1
if needle in haystack:
l1=len(haystack)
l2=len(needle)
while i<l1 and j <=l2:
if haystack[i] == needle[j]:
i+=1
j+=1
else:
i=i-j+1
j=0
if j == l2:
return i-l2
最长公共前缀
编写一个函数来查找字符串数组中的最长公共前缀。
如果不存在公共前缀,返回空字符串 “”。
示例 1:
输入: ["flower","flow","flight"]
输出: "fl"
示例 2:
输入: ["dog","racecar","car"]
输出: ""
解释: 输入不存在公共前缀。
说明:
所有输入只包含小写字母 a-z 。
#判断是否为空
if not strs:
return ""
#在使用max和min的 时候已经把字符串比较了一遍
#当前列表的字符串中,每个字符串从第一个字母往后比较直至出现ASCII码 最小的字符串
s1 = min(strs)
print(s1)
# 当前列表的字符串中,每个字符串从第一个字母往后比较直至出现ASCII码 最大的字符串
s2 = max(strs)
print(s2)
# 使用枚举变量s1字符串的每个字母和下标
for i,c in enumerate(s1):
if c !=s2[i]:
return s1[:i]
return s1
外观数列
「外观数列」是一个整数序列,从数字 1 开始,序列中的每一项都是对前一项的描述。前五项如下:
-
1 -
11 -
21 -
1211 -
111221
1 被读作 “one 1” (“一个一”) , 即 11。
11 被读作 “two 1s” (“两个一”), 即 21。
21 被读作 “one 2”, “one 1” (“一个二” , “一个一”) , 即 1211。
给定一个正整数 n(1 ≤ n ≤ 30),输出外观数列的第 n 项。
注意:整数序列中的每一项将表示为一个字符串。
示例 1:
输入: 1
输出: "1"
解释:这是一个基本样例。
示例 2:
输入: 4
输出: "1211"
解释:当 n = 3 时,序列是 “21”,其中我们有 “2” 和 “1” 两组,“2” 可以读作 “12”,也就是出现频次 = 1 而 值 = 2;类似 “1” 可以读作 “11”。所以答案是 “12” 和 “11” 组合在一起,也就是 “1211”。
有问题
链表
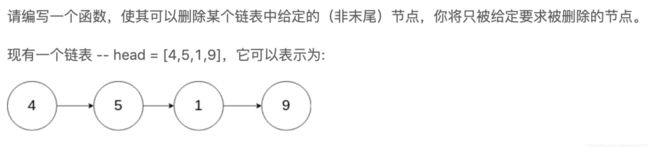
删除链表中的节点
输入: head = [4,5,1,9], node = 5
输出: [4,1,9]
解释: 给定你链表中值为 5 的第二个节点,那么在调用了你的函数之后,该链表应变为 4 -> 1 -> 9.
示例 2:
输入: head = [4,5,1,9], node = 1
输出: [4,5,9]
解释: 给定你链表中值为 1 的第三个节点,那么在调用了你的函数之后,该链表应变为 4 -> 5 -> 9.
说明:
链表至少包含两个节点。
链表中所有节点的值都是唯一的。
给定的节点为非末尾节点并且一定是链表中的一个有效节点。
不要从你的函数中返回任何结果。
# Definition for singly-linked list.
# class ListNode(object):
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution(object):
def deleteNode(self, node):
"""
:type node: ListNode
:rtype: void Do not return anything, modify node in-place instead.
"""
node.val = node.next.val
node.next = node.next.next
删除链表的倒数第N个节点
给定一个链表,删除链表的倒数第 n 个节点,并且返回链表的头结点。
示例:
给定一个链表: 1->2->3->4->5, 和 n = 2.
当删除了倒数第二个节点后,链表变为 1->2->3->5.
说明:
给定的 n 保证是有效的。
进阶:
你能尝试使用一趟扫描实现吗?
快慢指针:
class Solution(object):
def removeNthFromEnd(self, head, n):
"""
:type head: ListNode
:type n: int
:rtype: ListNode
"""
p = head
fast,slow = p,p
while n > 0 and fast.next != None:
n -= 1
fast = fast.next
if fast == None:
return p.next
while fast and fast.next:
fast = fast.next
slow = slow.next
slow.next = slow.next.next
return p
反转链表
反转一个单链表。
示例:
输入: 1->2->3->4->5->NULL
输出: 5->4->3->2->1->NULL
进阶:
你可以迭代或递归地反转链表。你能否用两种方法解决这道题?
方法一:
使用一个字典辅助
# Definition for singly-linked list.
# class ListNode(object):
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution(object):
def reverseList(self,head):
if head == None or head.next == None:
return head
p = head
d = {}
i=0
while p != None:
d[i]=p
p=p.next
i+=1
l=len(d)
for i in range(l-1,0,-1):
d[i].next = d[i-1]
d[0].next = None
return d[l-1]
方法二:
不使用外部空间辅助
# Definition for singly-linked list.
# class ListNode(object):
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution(object):
def reverseList(self,head):
if head is None:
return None
cur = head
pre = None
nxt = cur.next
while(nxt):
cur.next = pre
pre = cur
cur = nxt
nxt = nxt.next
cur.next = pre
head = cur
return head
合并两个有序链表
递归法:
class ListNode(object):
def __init__(self,x):
self.val = x
self.next = None
class Solution(object):
def mergeTwoLists(self,l1,l2):
if l1 == None:
return l2
if l2 == None:
return l1
if l1.val < l2.val:
l1.next = self.mergeTwoLists(l1.next,l2)
return l1
else :
l2.next = self.mergeTwoLists(l1,l2.next)
return l2
回文链表
请判断一个链表是否为回文链表。
示例 1:
输入: 1->2
输出: false
示例 2:
输入: 1->2->2->1
输出: true
进阶:
你能否用 O(n) 时间复杂度和 O(1) 空间复杂度解决此题?
# Definition for singly-linked list.
# class ListNode(object):
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution(object):
def isPalindrome(self,head):
if head == None or head.next == None:
return True
l = []
p = head
while(p.next):
l.append(p.val)
p = p.next
l.append(p.val)
return l == l[::-1]
环形链表
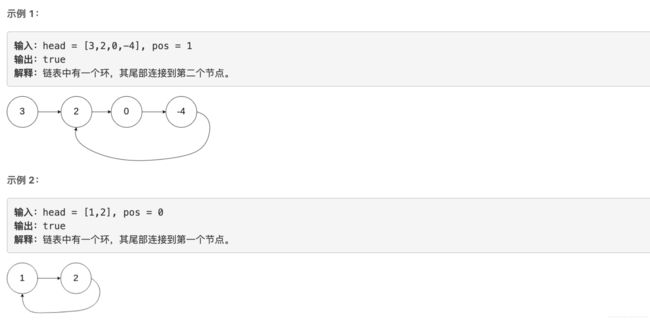
给定一个链表,判断链表中是否有环。
为了表示给定链表中的环,我们使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。 如果 pos 是 -1,则在该链表中没有环。

class Solution(object):
def hasCycle(self, head):
"""
:type head: ListNode
:rtype: bool
"""
if head == None or head.next == None:
return False
fast = slow = head
while fast and fast.next:
slow = slow.next
fast = fast.next.next
if slow == fast:
return True
return False
树
Python实现
二叉树的最大深度
给定一个二叉树,找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
示例:
给定二叉树 [3,9,20,null,null,15,7],

class TreeNode(object):
def __init__(self,x):
self.val = x
self.left = None
self.right = None
class Solution(object):
def maxDepth(self,root):
if root == None:
return 0
return max(self.maxDepth(root.left),self.maxDepth(root.right))+1
验证二叉搜索树
给定一个二叉树,判断其是否是一个有效的二叉搜索树。
假设一个二叉搜索树具有如下特征:
节点的左子树只包含小于当前节点的数。
节点的右子树只包含大于当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。

方法一:
对于二叉搜索树,我们可以通过中序遍历得到一个递增的有序序列。
class TreeNode(object):
def __init__(self,x):
self.val = x
self.left = None
self.right =None
class Solution(object):
def isValidBST(self,root):
def inorderTraversal(root):
if root == None:
return []
res = []
res+=inorderTraversal(root.left)
res.append(root.val)
res += inorderTraversal(root.right)
return res
res = inorderTraversal(root)
return res == sorted(list(set(res)))
方法二:
如果左子树的值小于根的值并且右子树的值大于根的值,并进行递归,成立则为二叉搜索树,否则则不是。
class Solution2(object):
def helper(self,root,min,max):
if root == None:
return True
if min is not None and root.val <= min:
return False
if max is not None and root.val >= max:
return False
if self.helper(root.left,min,root.val) and self.helper(root.right,root.val,max):
return True
else:
return False
def isValidBST(self,root):
min=max=None
return self.helper(root,min,max)
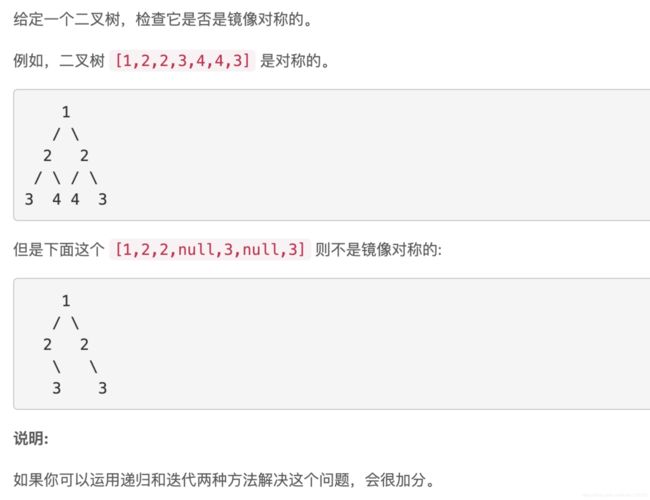
对称二叉树
class TreeNode(object):
def __init__(self,x):
self.val = x
self.left = None
self.right = None
class Solution(object):
def isSymmetric(self, root):
"""
:type root: TreeNode
:rtype: bool
"""
def isSameTree(p,q):
if not p and not q:
return True
if p and q and p.val == q.val:
l = isSameTree(p.left,q.right)
r = isSameTree(p.right,q.left)
return l and r
else:
return False
if root == None:
return True
else:
return isSameTree(root.left,root.right)
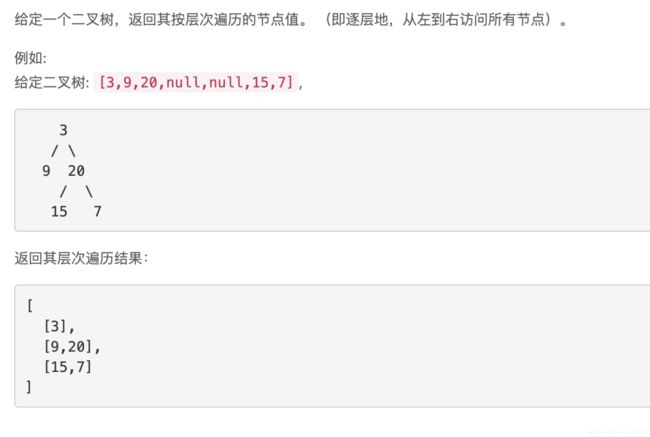
二叉树的层次遍历
class TreeNode(object):
def __init__(self,x):
self.val = x
self.left = None
self.right = None
class Solution(object):
def levelOrder(self,root):
"""
:type root: TreeNode
:rtype: List[List[int]]
"""
if root == None:
return []
res = []
level = [root]
while level:
res.append([node.val for node in level])
temp = []
for node in level:
temp.extend([node.left,node.right])
level = [leaf for leaf in temp if leaf]
return res
将有序数组转换为二叉搜索树
class TreeNode(object):
def __init__(self, x):
self.val = x
self.left = None
self.right = None
class Solution(object):
def sortedArrayToBST(self, nums):
"""
:type nums: List[int]
:rtype: TreeNode
"""
if not nums:
return None
if len(nums) == 1:
return TreeNode(nums[0])
mid = len(nums)//2
root = TreeNode(nums[mid])
root.left = self.sortedArrayToBST(nums[:mid])
root.right = self.sortedArrayToBST(nums[mid+1:])
return root
排序和搜索
Python实现
合并两个有序数组
给定两个有序整数数组 nums1 和 nums2,将 nums2 合并到 nums1 中,使得 num1 成为一个有序数组。
说明:
初始化 nums1 和 nums2 的元素数量分别为 m 和 n。
你可以假设 nums1 有足够的空间(空间大小大于或等于 m + n)来保存 nums2 中的元素。
示例:
输入:
nums1 = [1,2,3,0,0,0], m = 3
nums2 = [2,5,6], n = 3
输出: [1,2,2,3,5,6]
方法一:
class Solution(object):
def merge(self, nums1, m, nums2, n):
"""
:type nums1: List[int]
:type m: int
:type nums2: List[int]
:type n: int
:rtype: None Do not return anything, modify nums1 in-place instead.
"""
while n>0 and m>0:
if nums1[m-1]>=nums2[n-1]:
nums1[m+n-1] = nums1[m-1]
m-=1
else:
nums1[m+n-1] = nums2[n-1]
n-=1
if m == 0:
for i in range(n):
nums1[i] = nums2[i]
方法二:
class Solution2(object):
def merge(self,nums1,m,nums2,n):
nums1[m:m+n] = nums2[:]
nums1.sort()
return nums1
第一个错误的版本
你是产品经理,目前正在带领一个团队开发新的产品。不幸的是,你的产品的最新版本没有通过质量检测。由于每个版本都是基于之前的版本开发的,所以错误的版本之后的所有版本都是错的。
假设你有 n 个版本 [1, 2, …, n],你想找出导致之后所有版本出错的第一个错误的版本。
你可以通过调用 bool isBadVersion(version) 接口来判断版本号 version 是否在单元测试中出错。实现一个函数来查找第一个错误的版本。你应该尽量减少对调用 API 的次数。
示例:
给定 n = 5,并且 version = 4 是第一个错误的版本。
调用 isBadVersion(3) -> false
调用 isBadVersion(5) -> true
调用 isBadVersion(4) -> true
所以,4 是第一个错误的版本。
# The isBadVersion API is already defined for you.
# @param version, an integer
# @return a bool
# def isBadVersion(version):
class Solution(object):
def firstBadVersion(self, n):
"""
:type n: int
:rtype: int
"""
begain,end = 1,n
while begain < end:
mid = (begain+end)//2
if isBadVersion(mid):
end = mid
else:
begain = mid+1
return begain
动态规划
Python实现
爬楼梯
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
注意:给定 n 是一个正整数。
示例 1:
输入: 2
输出: 2
解释: 有两种方法可以爬到楼顶。
-
1 阶 + 1 阶
-
2 阶
示例 2:输入: 3
输出: 3
解释: 有三种方法可以爬到楼顶。 -
1 阶 + 1 阶 + 1 阶
-
1 阶 + 2 阶
-
2 阶 + 1 阶
class Solution(object):
def climbStairs(self, n):
"""
:type n: int
:rtype: int
"""
dp = [-1]*(n+1)
if n <=2:
return n
dp[0] = 1
dp[1] = 1
for i in range(2,n+1):
dp[i] = dp[i-1]+dp[i-2]
return dp[n]
买卖股票的最佳时机
给定一个数组,它的第 i 个元素是一支给定股票第 i 天的价格。
如果你最多只允许完成一笔交易(即买入和卖出一支股票),设计一个算法来计算你所能获取的最大利润。
注意你不能在买入股票前卖出股票。
示例 1:
输入: [7,1,5,3,6,4]
输出: 5
解释: 在第 2 天(股票价格 = 1)的时候买入,在第 5 天(股票价格 = 6)的时候卖出,最大利润 = 6-1 = 5 。
注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格。
示例 2:
输入: [7,6,4,3,1]
输出: 0
解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。
遍历法:(超出时间限制)
class Solution(object):
def maxProfit(self, prices):
"""
:type prices: List[int]
:rtype: int
"""
profit=0
for i in range(len(prices)):
for j in range(i):
if prices[i] - prices[j] > profit:
profit = prices[i]-prices[j]
return profit
动态规划:
用一个变量min_buy_prices记录下左侧的最小值,
转移方程
dp [i] = max(dp[i-1],min_buy_prices)
class Solution(object):
def maxProfit(self, prices):
"""
:type prices: List[int]
:rtype: int
"""
if not prices:
return 0
min_buy_prices = prices[0]
dp = [0]
profit = 0
for i in range(1,len(prices)):
min_buy_prices = min(min_buy_prices,prices[i])
dp.append(max(dp[i-1],prices[i]-min_buy_prices))
if dp[-1] > profit:
profit = dp[-1]
return profit
最大子序和
给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
示例:
输入: [-2,1,-3,4,-1,2,1,-5,4],
输出: 6
解释: 连续子数组 [4,-1,2,1] 的和最大,为 6。
进阶:
如果你已经实现复杂度为 O(n) 的解法,尝试使用更为精妙的分治法求解。
遍历法:
动态规划:
class Solution(object):
def maxSubArray(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
for i in range(1,len(nums)):
nums[i] = max(nums[i]+nums[i-1],nums[i])
return max(nums)
分治算法:
分治法,最大子序和要么在左半部分,要么在右半部分,要么就横跨两部分(即包括左半部分的最后一个元素,和右半部分的第一个元素)。返回这三种情况的最大值即可。第三种情况,其中包括左半部分最后一个元素的情形,需要挨个往前遍历,更新最大值。包含右半部分的第一个元素的情况类似。总的时间复杂度O(nlogn)
class Solution2(object):
def maxSubArray(self,nums):
#主函数
left = 0
right = len(nums)-1
maxSum = self.divide(nums,left,right)
return maxSum
def divide(self,nums,left,right):
if left == right:
return nums[left]
center = (left+right)//2
leftMaxSum = self.divide(nums,left,center)
rightMaxSum = self.divide(nums,center+1,right)
#求子序横跨2边的和,分成左边界和和右边界和
leftBoderSum = nums[center]
leftSum = nums[center]
for i in range(center-1,left-1,-1):
leftSum+=nums[i]
if leftSum>leftBoderSum:
leftBoderSum = leftSum
#不断更新左区域的最大值
rightBoderSum = nums[center+1]
rightSum = nums[center+1]
for i in range(center+2,right+1):
rightSum+=nums[i]
if rightSum > rightBoderSum:
rightBoderSum = rightSum
#不断更新右区域的最大值
#左边界+有边界的和
BoderSum = leftBoderSum+rightBoderSum
return max(leftMaxSum,rightMaxSum,BoderSum)
打家劫舍
你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组,计算你在不触动警报装置的情况下,能够偷窃到的最高金额。
示例 1:
输入: [1,2,3,1]
输出: 4
解释: 偷窃 1 号房屋 (金额 = 1) ,然后偷窃 3 号房屋 (金额 = 3)。
偷窃到的最高金额 = 1 + 3 = 4 。
示例 2:
输入: [2,7,9,3,1]
输出: 12
解释: 偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9),接着偷窃 5 号房屋 (金额 = 1)。
偷窃到的最高金额 = 2 + 9 + 1 = 12 。
class Solution(object):
def rob(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
last = 0
now = 0
for i in nums:
last, now = now, max(last + i, now)
#last = now
# now = max(last+i, now)
# last = now
return now
设计问题
Python实现
Shuffle an Array
import copy
import random
class Solution(object):
def __init__(self,nums):
self._item = nums
def reset(self):
return self._item
def shuffle(self):
res = []
temp = copy.deepcopy(self._item)
while len(temp) != 0:
toInsert = temp[random.randint(0,len(temp)-1)]
res.append(toInsert)
temp.remove(toInsert)
return res
最小栈
class Stack(object):
def __init__(self):
self.item = []
def push(self,x):
self.item.append(x)
def isEmpty(self):
return self.item == []
def pop(self):
if self.isEmpty():
raise Exception("Your stack is Empty!")
else:
return self.item.pop()
def top(self):
if self.isEmpty():
raise Exception("Your stack is Empty!")
else:
return self.item[len(self.item)-1]
def size(self):
return len(self.item)
class MinStack(object):
def __init__(self):
self.minStack = Stack()
self.dataStack = Stack()
def isEmpty(self):
return self.dataStack.isEmpty()
def push(self,x):
self.dataStack.push(x)
if self.minStack.isEmpty():
self.minStack.push(x)
elif self.minStack.top() >= x:
self.minStack.push(x)
def pop(self):
if self.isEmpty():
raise Exception("Your minStack is Empty")
else:
val = self.dataStack.pop()
if val == self.minStack.top():
self.minStack.pop()
def top(self):
return self.dataStack.top()
def size(self):
return self.dataStack.size()
def getMin(self):
return self.minStack.top()
数学
Python实现
Fizz Buzz
写一个程序,输出从 1 到 n 数字的字符串表示。
1. 如果 n 是3的倍数,输出“Fizz”;
2. 如果 n 是5的倍数,输出“Buzz”;
3.如果 n 同时是3和5的倍数,输出 “FizzBuzz”。
示例:
n = 15,
返回:
[
“1”,
“2”,
“Fizz”,
“4”,
“Buzz”,
“Fizz”,
“7”,
“8”,
“Fizz”,
“Buzz”,
“11”,
“Fizz”,
“13”,
“14”,
“FizzBuzz”
]
class Solution(object):
def fizzBuzz(self, n):
"""
:type n: int
:rtype: List[str]
"""
res = []
for i in range(1,n+1):
if i%3 ==0 and i%5 != 0:
res.append("Fizz")
elif i%5 ==0 and i%3 != 0:
res.append("Buzz")
elif i%3 == i%5 == 0:
res.append("FizzBuzz")
else:
res.append(str(i))
return res
计数质数
暴力法(超时了)
import math
class Solution(object):
def isPrime(self,num):
if num <=3:
return num >1
sqrt = int(math.sqrt(num))
for i in range(2,sqrt+1):
if num % i == 0:
return False
return True
def countPrimes(self, n):
"""
:type n: int
:rtype: int
"""
res = 0
for i in range(n):
if self.isPrime(i):
res += 1
return res
厄拉多塞筛法:
先将2-N的各数放入表中,然后在2的上面画一个圆圈,然后划去2的其他倍数;第一个既未画圈又没有被划去的数是3,将它画圈,再划去3的其他倍数;现在既未画圈又没有被划去的第一个数 是5,将它画圈,并划去5的其他倍数……依次类推,一直到所有小于或等于N的各数都画了圈或划去为止。这时,表中画了圈的以及未划去的那些数正好就是小于 N的素数。
在实现过程中,可以设置一个长度为n的数组,将所有值设为1.
然后从索引为2的数开始遍历数组,2是第一个质数,count加1,将所有索引2的倍数处的数置为0.直到2的倍数大于n为止
继续遍历数组,找到下一个不为0的数,count加1,将索引为该数字的倍数处的数字置为0,直到倍数大于n为止
import math
class Solution(object):
def isPrime(self,num):
if num <=3:
return num >1
sqrt = int(math.sqrt(num))
for i in range(2,sqrt+1):
if num % i == 0:
return False
return True
def countPrimes(self, n):
"""
:type n: int
:rtype: int
"""
res = 0
for i in range(n):
if self.isPrime(i):
res += 1
return res
3的幂
给定一个整数,写一个函数来判断它是否是 3 的幂次方。
示例 1:
输入: 27
输出: true
示例 2:
输入: 0
输出: false
示例 3:
输入: 9
输出: true
示例 4:
输入: 45
输出: false
进阶:
你能不使用循环或者递归来完成本题吗?
循环:
class Solution(object):
def isPowerOfThree(self,n):
"""
:type n: int
:rtype: bool
"""
while n > 0 :
if n %3 == 0:
n /= 3
else:
break
return True if n == 1 else False
后续挑战:
class Solution(object):
def isPowerOfThree(self, n):
"""
:type n: int
:rtype: bool
"""
return n>0 and 1162261467%n==0 #3^19=1162261467是小于2^31最大的3的倍数
罗马数字转整数
罗马数字包含以下七种字符: I, V, X, L,C,D 和 M。
字符 数值
I 1
V 5
X 10
L 50
C 100
D 500
M 1000
例如, 罗马数字 2 写做 II ,即为两个并列的 1。12 写做 XII ,即为 X + II 。 27 写做 XXVII, 即为 XX + V + II 。
通常情况下,罗马数字中小的数字在大的数字的右边。但也存在特例,例如 4 不写做 IIII,而是 IV。数字 1 在数字 5 的左边,所表示的数等于大数 5 减小数 1 得到的数值 4 。同样地,数字 9 表示为 IX。这个特殊的规则只适用于以下六种情况:
I 可以放在 V (5) 和 X (10) 的左边,来表示 4 和 9。
X 可以放在 L (50) 和 C (100) 的左边,来表示 40 和 90。
C 可以放在 D (500) 和 M (1000) 的左边,来表示 400 和 900。
给定一个罗马数字,将其转换成整数。输入确保在 1 到 3999 的范围内。
示例 1:
输入: "III"
输出: 3
示例 2:
输入: "IV"
输出: 4
示例 3:
输入: "IX"
输出: 9
示例 4:
输入: "LVIII"
输出: 58
解释: L = 50, V= 5, III = 3.
示例 5:
输入: "MCMXCIV"
输出: 1994
解释: M = 1000, CM = 900, XC = 90, IV = 4.
class Solution(object):
def romanToInt(self, s):
"""
:type s: str
:rtype: int
"""
d = {'I':1,'V':5,'X':10,'L':50,'C':100,'D':500,'M':1000}
result = 0
i = 0
while i < len(s)-1:
if d[s[i]] >= d[s[i+1]]:
result+= d[s[i]]
i+=1
else:
temp = d[s[i+1]]-d[s[i]]
result+=temp
i+=2
if i == len(s)-1:
result+=d[s[i]]
return result if 1 <= result <= 3999 else False
其他
Python实现
位1的个数
编写一个函数,输入是一个无符号整数,返回其二进制表达式中数字位数为 ‘1’ 的个数(也被称为汉明重量)。
示例 1:
输入:00000000000000000000000000001011
输出:3
解释:输入的二进制串 00000000000000000000000000001011 中,共有三位为 ‘1’。
示例 2:
输入:00000000000000000000000010000000
输出:1
解释:输入的二进制串 00000000000000000000000010000000 中,共有一位为 ‘1’。
示例 3:
输入:11111111111111111111111111111101
输出:31
解释:输入的二进制串 11111111111111111111111111111101 中,共有 31 位为 ‘1’。
提示:
请注意,在某些语言(如 Java)中,没有无符号整数类型。在这种情况下,输入和输出都将被指定为有符号整数类型,并且不应影响您的实现,因为无论整数是有符号的还是无符号的,其内部的二进制表示形式都是相同的。
在 Java 中,编译器使用二进制补码记法来表示有符号整数。因此,在上面的 示例 3 中,输入表示有符号整数 -3。
进阶:
如果多次调用这个函数,你将如何优化你的算法?
解法1:常规方法
class Solution(object):
def hammingWeight(self,n):
if n == 0:
return 0
while n > 0:
sum += n%2
n=n//2
return sum
解法2:通过python的 bin()函数 和 count()函数 来实现。
bin() 返回一个整数 int 或者长整数 long int 的二进制表示。
count() 方法用于统计字符串里某个字符出现的次数。可选参数为在字符串搜索的开始与结束位置。
class Solution(object):
def hammingWeight(self,n):
return bin(n).count('1')
解法3:通过 位运算 实现。
class Solution3(object):
def hammingWeight(self,n):
if n==0:
return 0
sum = 0
while n >0:
sum += n&1
# 相当于依次右移,然后计算下一位的值&1
n = n >> 1
return sum
汉明距离
class Solution(object):
def hammingDistance(self,x,y):
n = x^y
n = bin(n)
return n.count('1')
颠倒二进制位
颠倒给定的 32 位无符号整数的二进制位。
示例 1:
输入: 00000010100101000001111010011100
输出: 00111001011110000010100101000000
解释: 输入的二进制串 00000010100101000001111010011100 表示无符号整数 43261596,
因此返回 964176192,其二进制表示形式为 00111001011110000010100101000000。
示例 2:
输入:11111111111111111111111111111101
输出:10111111111111111111111111111111
解释:输入的二进制串 11111111111111111111111111111101 表示无符号整数 4294967293,
因此返回 3221225471 其二进制表示形式为 10101111110010110010011101101001。
提示:
请注意,在某些语言(如 Java)中,没有无符号整数类型。在这种情况下,输入和输出都将被指定为有符号整数类型,并且不应影响您的实现,因为无论整数是有符号的还是无符号的,其内部的二进制表示形式都是相同的。
在 Java 中,编译器使用二进制补码记法来表示有符号整数。因此,在上面的 示例 2 中,输入表示有符号整数 -3,输出表示有符号整数 -1073741825。
class Solution:
def reverseBits(self, n):
one=1
res=0
for i in range(32):
res=(res<<1)+(n&one)
n=n>>1
return res
缺失数字
给定一个包含 0, 1, 2, …, n 中 n 个数的序列,找出 0 … n 中没有出现在序列中的那个数。
示例 1:
输入: [3,0,1]
输出: 2
示例 2:
输入: [9,6,4,2,3,5,7,0,1]
输出: 8
说明:
你的算法应具有线性时间复杂度。你能否仅使用额外常数空间来实现?
解法1: 最常规做法, nums排序的sort()函数, 然后找位置插入
class Solution(object):
def missingNumber(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
if len(nums) == 1 and nums[-1] == 0:
return 1
if len(nums) >= 1 and 0 not in nums:
return 0
nums.sort()
for i in range(len(nums)-1):
if nums[i+1] - nums[i] ==2:
return nums[i]+1
if len(nums) > 1 and nums[-1] -nums[-2] ==1:
return nums[-1]+1
解法2:通过枚举法,sort()函数 + enumerate()函数
enumerate() 函数用于将一个可遍历的数据对象(如列表、元组或字符串)组合为一个索引序列,同时列出数据和数据下标,一般用在 for 循环当中。
enumerate(sequence, [start=0])
class Solution(object):
def missingNumber(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
nums,sort()
for key,value in enummerate(nums):
if key != value:
return key
else:
return key+1
解法3:数学方法,等差数列的性质
思路:nums相当于一个等差数列减去某一个数, 所以用该等差数列的和减去nums的和即为所求。
等差数列求和公式:Sn = n*a1+n(n-1)d/2 或 Sn = n(a1+an)/2。
class Solution3(object):
def missingNumber(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
# int(len(nums) * (len(nums)+1)/2 为等差数列的和
# sum(nums)为列表的的和
# 二者的差值即为缺失值
return (int(len(nums) * (len(nums) + 1) / 2) - sum(nums))
解法4: 位运算
class Solution4(object):
def missingNumber(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
bit = 0
for i,j in enumerate(nums):
bit ^= i ^j
return bit^len(nums)
解法5:set()函数
class Solution(object):
def missingNumber(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
return (set(range(len(nums) + 1)) - set(nums)).pop()
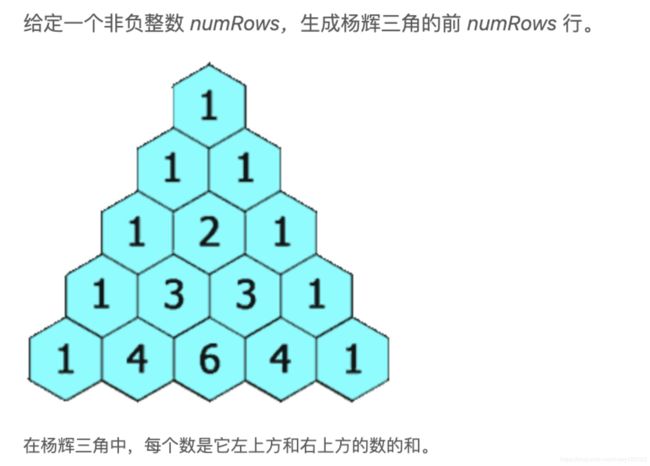
class Solution(object):
def generate(self, numRows):
"""
:type numRows: int
:rtype: List[List[int]]
"""
res = []
for i in range(numRows):
temp = [1]*(i+1)
res.append(temp)
for j in range(1,i):
res[i][j] = res[i-1][j-1] + res[i-1][j]
return res
有效括号
class Stack(object):
def __init__(self):
self.data = []
def isEmpty(self):
return self.data == []
def push(self,x):
self.data.append(x)
def pop(self):
if self.isEmpty():
raise Exception("Your Stack is Empty!")
else:
return self.data.pop()
def top(self):
if self.isEmpty():
raise Exception("Your Stack is Empty!")
else:
return self.data[len(self.data)-1]
def size(self):
return len(self.data)
class Solution(object):
def isValid(self,s):
"""
:type s: str
:rtype: bool
"""
stack = Stack()
d = {'(':')','{':'}','[':']'}
if len(s)%2 != 0:
return False
for i in s:
if i in d.keys():
stack.push(i)
elif stack.isEmpty() and i in d.values():
return False
elif i in d.values() and i == d[stack.top()]:
stack.pop()
return stack.isEmpty()