python实现决策树生成算法ID3、C4.5

有用请点赞，没用请差评。

欢迎分享本文，转载请保留出处。

 

目录

 决策树原理

    决策树模型

 决策树生成算法python实现

  

前言：

本章节实现了ID3和C4.5的决策树生成算法，决策树的剪枝请参考下一篇博客。算法是基于李航老师的《统计学习方法》，相关公式在代码中都分别标注了。博客内容参考于李航老师《统计学习方法》和某位大佬的博客https://blog.csdn.net/c406495762/article/details/75663451

 

一 决策树原理

1、决策树模型

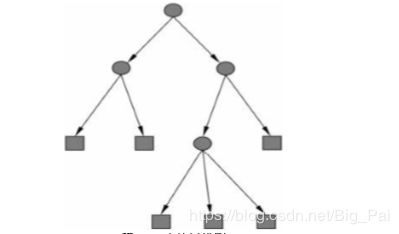
决策树是一种基本的分类与回归方法。决策树模型呈树形结构，在分类过程中表示基于特征对实例进行分类的过程，可以认为是if-then规则的集合。分类决策树由结点（node）和有向边组成。结点有两种类型：内部结点和叶结点。内部结点表示一个特征或者属性，叶结点表示一个类。如下图，图中圆和方框分别表示内部结点和叶结点，箭头表示有向边。

 我们可以把决策树看成一个if-then规则的集合，将决策树转换成if-then规则的过程是这样的：由决策树的根结点(root node)到叶结点(leaf node)的每一条路径构建一条规则；路径上内部结点的特征对应着规则的条件，而叶结点的类对应着规则的结论。决策树的路径或其对应的if-then规则集合具有一个重要的性质：互斥并且完备。这就是说，每一个实例都被一条路径或一条规则所覆盖，而且只被一条路径或一条规则所覆盖。这里所覆盖是指实例的特征与路径上的特征一致或实例满足规则的条件。

2、决策树计算

 

 

 

   ID3算法 

 

C4.5算法 

 

 

 二决策树生成算法的实现

采用的数据集：

                                                          贷款申请样本数据表

ID	年龄	有工作	有自己的房子	信贷情况	类别(是否个给贷款)
1	青年	否	否	一般	否
2	青年	否	否	好	否
3	青年	是	否	好	是
4	青年	是	是	一般	是
5	青年	否	否	一般	否
6	中年	否	否	一般	否
7	中年	否	否	好	否
8	中年	是	是	好	是
9	中年	否	是	非常好	是
10	中年	否	是	非常好	是
11	老年	否	是	非常好	是
12	老年	否	是	好	是
13	老年	是	否	好	是
14	老年	是	否	非常好	是
15	老年	否	否	一般	否

源码：

# -*- coding:utf-8 -*-
# Decision tree 决策树，ID3\C4.5算法，算法参考李航《统计学习方法》
#author:Tomator


import numpy as np
import math


# 测试数据集，《统计学习方法》P59，贷款申请样本数据集
def createDataSet():
    dataSet = [[0, 0, 0, 0, 'no'],                        #数据集
            [0, 0, 0, 1, 'no'],
            [0, 1, 0, 1, 'yes'],
            [0, 1, 1, 0, 'yes'],
            [0, 0, 0, 0, 'no'],
            [1, 0, 0, 0, 'no'],
            [1, 0, 0, 1, 'no'],
            [1, 1, 1, 1, 'yes'],
            [1, 0, 1, 2, 'yes'],
            [1, 0, 1, 2, 'yes'],
            [2, 0, 1, 2, 'yes'],
            [2, 0, 1, 1, 'yes'],
            [2, 1, 0, 1, 'yes'],
            [2, 1, 0, 2, 'yes'],
            [2, 0, 0, 0, 'no']]
    labels = ['年龄', '有工作', '有自己的房子', '信贷情况']		#特征标签
    return dataSet, labels                             #返回数据集和特征标签

# 计算经验熵，《统计学习方法》P62，公式5.7
def cal_empirical_entropy(data_vector):
    nums_data=len(data_vector)   #数据集样本数
    counts_by_labels={}      #用来保存每个label下的样本数
    entroy=0
    for vector in data_vector:
        if vector[-1] not in counts_by_labels:       #vector[-1]为label值
            counts_by_labels[vector[-1]]=0
        counts_by_labels[vector[-1]]+=1              #统计label出现的次数
    for key in counts_by_labels:
        p=float(counts_by_labels[key]/nums_data)          #计算每个标签出现的概率
        entroy-=p*math.log(p,2)                     #计算经验熵，公式5.7
    return entroy

"""
根据每个特征划分数据集
data_vector
index_feature：特征的索引位置i
value：用来划分的特征取值

返回划分后的子数据及样本数，和子数据集（子数据集剔除了第i列特征）
"""
def split_datatset(data_vector,index_feature,value):
    split_set=[]
    for vector in data_vector:
        # 挑选vector[index_feature]==value的数据
        if vector[index_feature]==value:
            # 去掉第i列特征
            split_1=vector[:index_feature]
            split_1.extend(vector[index_feature+1:])
            split_set.append(split_1)
    return len(split_set),split_set

# 用于返回fea_x1,max_x2中较大一方所对应的值和索引位置。
def choose_max(fea_x1,max_x2,fea_index1,max_indx2):
    if fea_x1>max_x2:
        return fea_x1,fea_index1
    else:
        return max_x2,max_indx2

# 选择最优分类特征
# create_alg_para，生成决策树的方法：ID3或者C45
def choose_bestfeture(data_vector,create_alg_para):
    nums_data=len(data_vector)
    nums_feature=len(data_vector[0])-1              #每个样本所包含的特征个数
    empirical_entropy=cal_empirical_entropy(data_vector)   #计算经验熵
    max_information_gain=0                     #表示最大信息增益
    max_information_gain_ratio=0                 #表示最大的信息增益比
    best_index_feature=0                         #表示最优特征的索引位置index
    for i in range(nums_feature):                #遍历所有的特征
        features_i_set=[vector[i] for vector in data_vector]           #提取第i个特征中所包含的可能取值
        features_i_set=set(features_i_set)             #对特征值去重
        conditional_entroy=0                        #表示每个特征的经验条件熵，公式5.8
        ha_d_entroy=0                                      #表示数据集D关于特征A的值的熵Ha(D)，公式5.10
        for fea in features_i_set:                 #遍历第i个特征的所有vlaue
            nums_di,di_set=split_datatset(data_vector,i,fea)     #
            p_di=nums_di/nums_data                 #计算|Di|/|D|，公式5.8
            ha_d_entroy-=p_di*math.log(p_di,2)     #计算数据集D关于特征A的值的熵Ha(D)，参考公式5.10
            entroy_di=cal_empirical_entropy(di_set)   #计算子类的经验熵，公式5.8中的H(Di)
            conditional_entroy+=p_di*entroy_di
        fea_information_gain=empirical_entropy-conditional_entroy    #计算每个特征对应的信息增益，公式5.9
        fea_information_gain_ratio=fea_information_gain/ha_d_entroy   #计算每个特征对应的信息增益比，公式5.10
        # print(i,fea_information_gain)

        # 选择最大的信息增益或者信息增益比所对应的特征索引位置
        # 通过create_alg_para参数选择是ID3还是C4.5算法。
        if create_alg_para == "ID3":
            max_information_gain,best_index_feature=choose_max(fea_information_gain,max_information_gain,i,best_index_feature)
        elif create_alg_para == "C45":
            max_information_gain_ratio,best_index_feature=choose_max(fea_information_gain_ratio,max_information_gain_ratio,i,best_index_feature)
        else:
            exit("create_alg_para should be 'ID3' or 'C45'.")

    return best_index_feature          #返回最优分类特征的索引位置

# 返回类列表中出现次数最多的类标签
def max_class(label_list):
    count_label={}
    for label in label_list:
        if label not in count_label:
            count_label[label]=0
        count_label[label]+=1
    #     选择字典value最大的所对应的key值
    return max(count_label,key=count_label.get)



# 决策树的生成
class Decision_tree(object):
    def __init__(self,data_vector,labels,create_alg_para='C45'):
        # 数据集
        self.data_vector=data_vector
        # 特征标签
        self.labels=labels
        # 生成决策树的方法：ID3或者C45
        self.create_alg_para=create_alg_para

    # 生成决策树，返回决策树tree，字典形式
    def tree_main(self):
        tree=self.create_decision_tree(self.data_vector,self.labels)
        return tree


    """
    递归函数，用于生成每一个子树,并返回。
    《统计学习方法》ID3或C4.5算法
    data_vector：每一个待分类数据集
    labels：待分类特征标签 
    
    """
    def create_decision_tree(self,data_vector,labels):
        nums_label=[vector[-1] for vector in data_vector]
        # 如果数据集中所有实例属于同一个类，则停止划分。返回该类 标签。
        if len(set(nums_label))==1:
            return nums_label[0]
        # print("a",'\n',data_vector)
        # 如果特征集只有一类时，即已经遍历完了所有特征，则停止划分。返回出现次数最多的类标签
        if len(data_vector[0])==1:
            return max_class(nums_label)

        best_index_feature=choose_bestfeture(data_vector,self.create_alg_para)    #选择最优特征
        best_feature_label=labels[best_index_feature]         #最优特征的标签
        myTree = {best_feature_label: {}}                    #子决策树，key为最优特征的标签，value为子决策树
        del (labels[best_index_feature])                    #删除已经使用过的最优特征标签
        best_feature_value = [vector[best_index_feature] for vector in data_vector]
        best_feature_set = set(best_feature_value )
        # 根据最优特征标签的属性值划分新的子数据集，并递归生成子树
        for f_value in best_feature_set:
            nums_data_vector,data_vector_split=split_datatset(data_vector,best_index_feature,f_value)
            myTree[best_feature_label][f_value]=self.create_decision_tree(data_vector_split,labels)
        return  myTree

    def cart(self):
        # CART算法参考下一篇博客
        pass

if __name__ == '__main__':
    dataSet, labels = createDataSet()
    # best=choose_bestfeture(dataSet)
    # print(best)

    # create_alg_para should be 'ID3' or 'C45'
    tree=Decision_tree(dataSet,labels,create_alg_para="C45")
    print(tree.tree_main())

 输出：