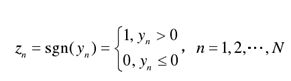LDPC码

LDPC码简介

低密度校验码（LDPC码）是一种前向纠错码，LDPC码最早在20世纪60年代由Gallager在他的博士论文中提出，但限于当时的技术条件，缺乏可行的译码算法，此后的35年间基本上被人们忽略，其间由Tanner在1981年推广了LDPC码并给出了LDPC码的图表示，即后来所称的Tanner图。1993年Berrou等人发现了Turbo码，在此基础上，1995年前后MacKay和Neal等人对LDPC码重新进行了研究，提出了可行的译码算法，从而进一步发现了LDPC码所具有的良好性能，迅速引起强烈反响和极大关注。经过十几年来的研究和发展，研究人员在各方面都取得了突破性的进展，LDPC码的相关技术也日趋成熟，甚至已经开始有了商业化的应用成果，并进入了无线通信等相关领域的标准。

1.1.1 LDPC码的特点

LDPC码是一种分组码，其校验矩阵只含有很少量非零元素。正是校验矩阵的这种稀疏性，保证了译码复杂度和最小码距都只随码长呈现线性增加。除了校验矩阵是稀疏矩阵外，码本身与任何其它的分组码并无二致。其实如果现有的分组码可以被稀疏矩阵所表达，那么用于码的迭代译码算法也可以成功的移植到它身上。然而，一般来说，为现有的分组码找到一个稀疏矩阵并不实际。不同的是，码的设计是以构造一个校验矩阵开始的，然后才通过它确定一个生成矩阵进行后续编码。而LDPC的编码就是本文所要讨论的主体内容。

译码方法是LDPC码与经典的分组码之间的最大区别。经典的分组码一般是用ML类的译码算法进行译码的，所以它们一般码长较小，并通过代数设计以减低译码工作的复杂度。但是LDPC码码长较长，并通过其校验矩阵H的图像表达而进行迭代译码，所以它的设计以校验矩阵的特性为核心考虑之一。

1.1.2 LDPC码的构造

构造二进制LDPC码实际上就是要找到一个稀疏矩阵H作为码的校验矩阵，基本方法是将一个全零矩阵的一小部分元素替换成1，使得替换后的矩阵各行和各列具有所要求的数目的非零元素。如果要使构造出的码可用，则必须满足几个条件，分别是无短环，无低码重码字，码间最小距离要尽可能大。

1.1.3 Tanner图

LDPC码常常通过图来表示，而Tanner图所表示的其实是LDPC码的校验矩阵。Tanner图包含两类顶点:n个码字比特顶点(称为比特节点)，分别与校验矩阵的各列相对应和m个校验方程顶点(称为校验节点)，分别与校验矩阵的各行对应。校验矩阵的每行代表一个校验方程，每列代表一个码字比特。所以，如果一个码字比特包含在相应的校验方程中，那么就用一条连线将所涉及的比特节点和校验节点连起来，所以Tanner图中的连线数与校验矩阵中的1的个数相同。以下图是矩阵

的Tanner图，其中比特节点用圆形节点表示，校验节点用方形节点表示，加黑线显示的是一个6循环：

Tanner图中的循环是由图中的一群相互连接在一起的顶点所组成的，循环以这群顶点中的一个同时作为起点和终点，且只经过每个顶点一次。循环的长度定义为它所包含的连线的数量，而图形的围长，也可叫做图形的尺寸，定义为图中最小的循环长度。如上图中，图形的尺寸，即围长为6，如加黑线所示。

1.2 LDPC编码

方法一：设H=[A | B]，对H进行高斯消元可得到H=[I| P]，设编码完成的码字为u=[c| s]，其中c为监督位，s为信息位。因为H*u' = u*H' = 0，可以得到I*c' + P*s' = 0 即 I*c' = P*s' (在GF(2)上)，从而可求 c' = P*s'。如果高斯消元过程中进行了列交换，则只需记录列交换，并以相反次序对编码后的码字同样进行列交换即可。解码时先求出u，再进行列交换得到u1=[c| s]，后面部分即是想要的信息。

方法一示例：

 

方法二：首先推导出根据校验矩阵直接编码的等式。将尺寸为m*n校验矩阵H写成如下形式：H=[H1 | H2]，其中H1矩阵的大小为m*k，H2的大小为m*m，设编码完成的码字为u=[s | p]，s为信息位，p为监督位。因为H*u' =u*H' = 0求得p*H2'=s*H1'，最后得p=s* H1'* (H2')-

上述两种方法可以不通过生成矩阵而直接由校验矩阵进行编码的等式,一切只依赖校验矩阵的编码都是通过这两个式子实现的。但方法二要考虑H2是否满秩（可逆）。

1.3 LDPC码H矩阵的构造

规则的LDPC码和非规则的LDPC码

如果校验矩阵中各行非零元素的个数相同，各列中非零元素的个数也相同，这样的LDPC码称为规则码，与规则码对照，如果校验矩阵的各行中非零元素的个数不同或各列中非零元素个数不同，此时的LDPC码称为非规则的LDPC码。

1.3.1 非规则的LDPC码

构造方法：码率R=M/N=0.5，构造的H矩阵列重固定，而行重是随机的。下面通过一个大小为6*12，列重为2的H矩阵来说明。因为列重固定为2，所以其列坐标集合为[1,1,2,2,3,3,4,4…….12,12]，而行坐标可以随机构造。

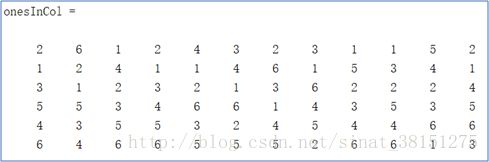
1.       先构造一个6*12，每一列为1到6随机排列的矩阵onesInCol。

2.       选取onesInCol的前2行（和列重一致），如上图所示。

3.        将所选取的矩阵按列依次排列如下

 

4.       构造矩阵tmp

5.       矩阵tmp重排成c1

6.       full 把稀疏矩阵转换为满阵显示， sparse 创建稀疏矩阵生成M*N阶稀疏矩阵H在以向量r1和c1为坐标的位置上的对应元素值为向量1的对应值。

1.3.2 规则的LDPC 码

对于码率R=0.5的规则的LDPC码其行重与列重有关，行重是列重的2倍。以6*12的H矩阵为例，假设其列重为2，每列1的个数为2，总的1的个数为2*12=24，H矩阵有6行，行重相同则每行1的个数为24/6=4，即行重为4。假设其列重为3，其行重为6。

构造方法：与构造行重类似，行重列重固定之后，其在矩阵中的位置坐标集合固定，如列重为2，行重为4，列坐标集合为[1，1，2，2，3，3，…..]，行坐标集合为[1,1,1,1,2,2,2,2,3,3,3,3,……]，下面考虑的就是如何将行列坐标组合起来而不重复。这里采用的是保持行坐标集合不变，列坐标集合打乱重排。以构造大小5*10，列重为2，行重为4的H矩阵为例说明。

1.       先构造一个5*10，每一列为1到5随机排列的矩阵onesInCol。

2.       选取onesInCol的前2行（和列重一致）构成1*20的矩阵

3.       将r按升序排列得到

4.       记录下排列前的位置索引

5.       因为列坐标集合为[1,1,2,2,3,3,4,4,……9,9,10,10]，将列坐标集合根据上面的位置索引重新排列，得到c

 

6.       行坐标集合如下，与列坐标一一对应，确定矩阵H中1的位置。

7.       最后结果

 

1.3.3 LDPC码的环

在 LDPC 码的 Tanner 图中，从一个顶点出发，经过不同顶点后回到同一个顶点的一些“边”组成的回路称为“环”。经过的边的个数称为环的长度。所有环中周长最小的环称为 LDPC码的围长(girth) ‎。

Tanner 图中的环不可避免的会对译码结果造成非常大的干扰。由于迭代概率译码会使信息在节点间交互传递，若存在环，从环的某一个节点出发的信息会沿着环上的节点不断传递并最终重新回到这个节点本身，从而使得节点自身信息不断累加，进而使得译码的最终结果失败的概率变大。显然，环长越小，信息传递回本身所需走的路径就越短，译码失败的概率就变得越高。Tanner 图形成一个环至少需要 4 个节点组成4 条相连的边，即环长最小为4，这类短环对码字的译码结果干扰最大。定义 LDPC码的行列(RC)约束为：两行或两列中不存在元素 1 的位置有 1 个以上相同的情况。显然，满足 RC 约束的 LDPC 码最低就是 6 环，去除了4 环的干扰。由于4环的检测以及避免最为简单并且必要，因此绝大部分构造方法都会满足 RC 约束。而构造大圈长的码字则需要精确的设计。

 

1.4 LDPC译码

Gallager 在描述 LDPC 码的时候，分别提出了硬判决译码算法和软判决译码算法两种。经过不断发展，如今的硬判决算法已在 Gallager 算法基础上进展很多，包含许多种加权比特翻转译码算法及其改进形式。硬判决和软判决各有优劣，可以适用于不同的应用场合。

1.4.1 比特翻转算法（BF）

硬判决译码算法最早是 Gallager 在提出 LDPC 码软判决算法时的一种补充。硬判决译码的基本假设是当校验方程不成立时，说明此时必定有比特位发生了错误，而所有可能发生错误的比特中不满足校验方程个数最多的比特发生错误的概率最大。在每次迭代时均翻转发生错误概率最大的比特并用更新之后的码字重新进行译码。具体步骤如下：

1.       设置初始迭代次数 k1及其上限kmax 。对获得的码字y=（y1，y2…yn）按照下式展开二元硬判决得到接收码字的硬判决序列Zn 。

2.       若k1=kmax ，则译码结束。不然，计算伴随式s=(s0,s1,…sm-1)，sm表示第m个校验方程的值。若伴随式的值均为 0，说明码字正确，译码成功。否则说明有比特位错误。继续进行步骤3。

3.       对每个比特，统计其不符合校验方程的数量fn （1<=n<=N）

4.       将最大fn所对应的比特进行翻转，然后k=k+1，返回步骤2。

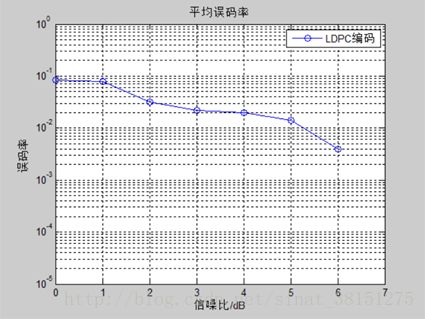
BF 算法的理论假设是若某个比特不满足校验方程的个数最多，则此比特是最有可能出错的比特，因此，选择这个比特进行翻转。BF 算法舍弃了每个比特位的可靠度信息，单纯的对码字进行硬判决，理论最为简单，实现起来最容易，但是性能也最差。当连续两次迭代翻转函数判断同一个比特位为最易出错的比特时，BF 算法会陷入死循环，大大降低了译码性能。

图50*100

图 500*1000

1.4.2 置信传播算法（BP）

置信传播(Belief Propagation)译码算法是消息传递(Message Passing)算法在 LDPC译码中的运用。消息传递算法是一个算法类，最初运用于人工智能领域，人们将其运用到 LDPC 码的译码算法中，提出了LDPC 码的置信传播算法。置信传播算法是基于 Tanner 图的迭代译码算法。在迭代过程中，可靠性信息，即“消息”通过 Tanner图上的边在变量节点和校验节点中来回传递，经多次迭代后趋于稳定值，然后据此进行最佳判决。

置信传播译码算法的基本流程如下：

在迭代前，译码器接收到信道传送过来的实值序列y=(y1,y2,….yn)，所有变量节点bi接收到对应的接收值yi。

第一次迭代：每个变量节点给所有与之相邻的校验节点传送一个可靠性消息，这个可靠性消息就是信道传送过来的值；每个校验节点接收到变量节点传送过来的可靠性消息之后，进行处理，然后返回一个新的可靠性信息给与之相邻的变量节点，这样就完成了第一次迭代；此时可以进行判决，如果满足校验方程，则不需要再迭代，直接输出判决结果，否则进行第二次迭代。

第二次迭代：每个变量节点处理第一次迭代完成时校验节点传送过来的可靠性消息，处理完成后新的消息发送给校验节点，同理，校验节点处理完后返回给变量节点，这样就完成了第二次迭代。完成后同样进行判决，如果满足校验方程则结束译码，否则如此反复多次迭代，每次都进行判决，直到达到设定的最大迭代次数，译码失败。在每次迭代过程中，无论是变量节点传送给校验节点的信息或者校验节点传送给变量节点的信息，都不应该包括前次迭代中接收方发送给发送方的信息，这样是为了保证发送的信息与接收节点已得到的信息相互对立。

 

                                                                                         图50*100

图500*1000

 

 

结束语

目前LDPC码研究领域的主要工作集中在译码算法的性能分析、编码方法、码的优化算法等，经过研究人员的努力，LDPC码的研究取得很大进展，但仍有许多问题需要进一步研究：

（1）LDPC码校验矩阵的构造，尽管在构造最优的LDPC码方面取得了一些进步，但目前还没有一套系统的办法来构造所需要的好码，特别是在码字长度有限、码率一定的条件下，构造性能优异的好码是一个非常具有挑战性的课题。

（2）LDPC编码系统的联合优化设计，将编码技术与调制技术、均衡技术、时空编码技术、OFDM技术结合进行性能优化是当前及将来的发展方向之一。

（3）无线衰落信道及MIMO技术下LDPC码的性能分析方法及优化设计准则。目前LDPC码字的优化设计主要在加性高斯白噪声信道下得到的，而无线衰落信道下，特别是时变信道非线性环境下码字的性能分析方法、优化设计准则和信道估计的影响也是非常关键的课题，需要进一步的研究探索。

此外，基于LDPC码的链路自适应技术，LDPC码在集成通信网物理层、应用层联合优化系统中的应用,LDPC码在无线局域网和深空宇航中的应用，基于LDPC码的图像传输、图像数字水印系统中的应用以及寻找更适合硬件实现的LDPC码编译码方法等都是非常值得研究的课题。