确知信号分析 | 通信原理仿真一

写在前面：
现代通信原理是电子系的一门专业必修课，介绍了通信原理系统的基本概念、基本原理、基本技术以及设计和分析的方法。俗话说得好，实践出真知。要想学好这门课，必要的动手实践是必不可少的。实践是基于Matlab上实现仿真的。Matlab具有函数丰富、语法简单易懂的特点，因此，很多高校在这门课上的实践都是要求学生在Matlab上实现的，作为学长，以一个过来人的身份告诉你们，有时间还是少打王者吃鸡，花点时间来系统的学习一下Matlab，毕竟在大三很多专业课都需要用到Matlab哦。

本次的仿真说简单简单，说难也难，主要是让大家熟悉一下Matlab的操作，还有复习一下信号与系统的知识。好了，废话不多说，咱们开始进入正题。

一、活动内容与目标

1、 掌握确知信号的原理
2、 掌握幅度谱的原理

二、实验的原理描述

[确知信号]

指其取值在任何时间都是确定的和可预知的信号，与其对应的是随机信号。确知信号通常可以用数学公式表示它在任何时间的取值。按照是否具有周期重复性，确知信号可以分为周期信号和非周期信号。按能量是否有限区分，信号可以分为能量信号和功率信号两类。

[幅度谱]

完整的频谱图应该包括幅度谱和相位谱。幅度谱是信号进行傅里叶级数变换或者傅里叶变换后的函数的模。在本实验中，由于需要绘制幅度谱的信号均为功率信号，所以幅度谱特指信号变换成傅里叶级数后的模。这里多说一点，很多人的信号与系统并没有学得很牢固，只知道，傅里叶级数和傅里叶变换均是研究信号在频谱时怎么样的工具。有兴趣的同学可以在网上看看别人的文章，都写得非常不错的。这里我们的信号为功率信号，更准确的说是周期信号，对于周期信号我们使用的工具就是傅里叶级数。

三、实验的任务和结果

(1)实现

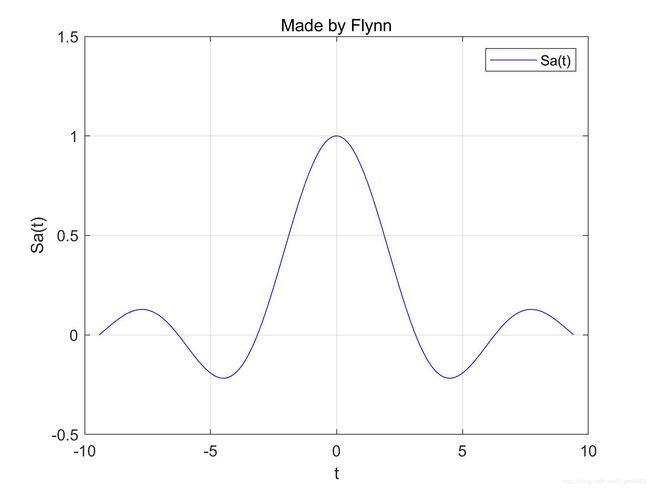
绘制Sa(t)的波形。

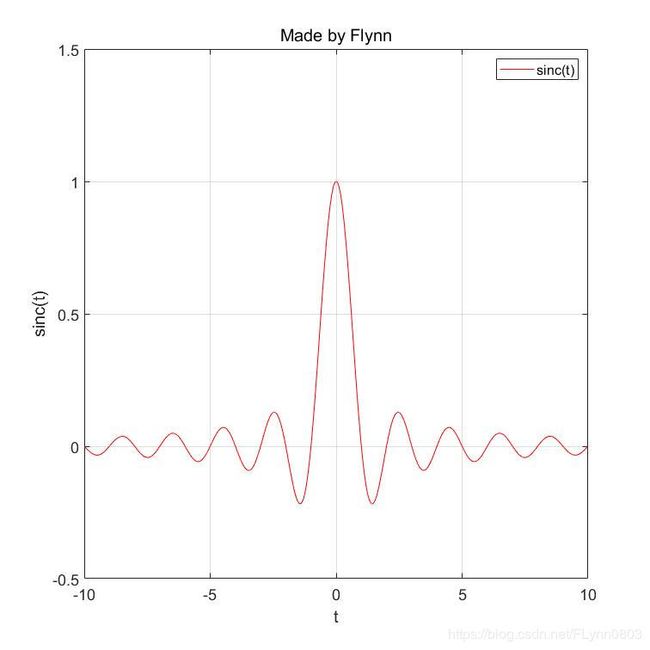
绘制sinc(t)的波形。

二维图形的绘制步骤（有些步骤不是必须的）：

1. 准备数据
2. 设置当前绘图区
3. 绘制图形
4. 设置图形中曲线和标记点的格式
5. 标记图形
6. 保存和导出图形

```python
clear all;
%(1)准备数据
t=-3*pi:0.01:3*pi;
ft=sin(t)./t;
%(2)设置当前绘图区
figure (1);
%(3)绘图并设置曲线
plot(t,ft,'b-');
%设置网格线属性和坐标轴
grid on;
axis([-10 10 -0.5 1.5]);
%标记图形
legend('Sa(t)');
xlabel("t");ylabel("Sa(t)");title("Made by Flynn")

(2)实现

绘制sinc(t)的波形

clear all;
%(1)准备数据
t=-10:0.01:10;
ft=sin(pi*t)./(pi*t);
%(2)设置当前绘图区
figure (1);
%(3)绘图并设置曲线
plot(t,ft,'r-');
%设置网格线属性和坐标轴
grid on;
axis([-10 10 -0.5 1.5]);
%标记图形
legend('sinc(t)');
xlabel("t");ylabel("sinc(t)");title("Made by Flynn")

(3)①如图所示周期矩形脉冲，试绘制其幅度谱。

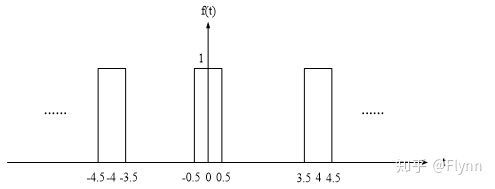
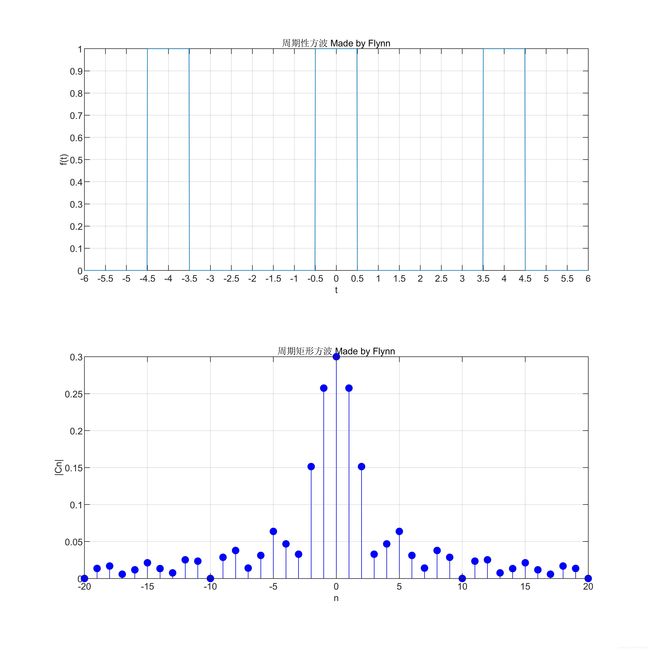
如图所示是一个功率信号，准确的说是一个周期矩形方波，其周期为4，宽度为1，幅度为1。要在频率域中分析这个信号我们需要要到傅里叶级数这个工具，得到的傅里叶级数一般为一个复数，这里我们需要的是幅度谱，因此我们用到abs()函数对结果取模。

首先我们复习一下傅里叶级数的公式：

再则，我们在介绍一下待会用到的数据处理的函数

square(t,duty)，这个MATLAB函数生成一个方波周期2π的元素时间数组t，duty为占空比，单位为“%”。我们本次的这个函数占空比就为25，这个函数画出的波形是双极性波形，转换为单极性波形的方法是整体向上平移后再除以2。

int(S,a,b)，是S对其符号变量从a到b的定积分。积分区间也可以使用带有两个元素的行或列向量来指定，即，有效的调用也是int(S，[a,b])或int(S，[a,b])和int(S，[a;b])。syms的作用是把字符或数字变成符号变量，一般在进行定积分的运算前都需要进行这步。

clear all
t=-6:0.01:6;
f=(square(2*pi/4*(t+0.5),25)+1)/2;
subplot(2,1,1);
%画出周期方波信号
plot(t,f);
set(gca,'xtick',-6:0.5:6); 
grid on;
xlabel('t');    
ylabel('f(t)'); 
title('周期性方波 Made by Flynn');
hold on;
%求周期方波的傅里叶级数
%syms的作用是把字符或数字变成字符，一般在进行定积分的运算前都需要进行这步
syms t1 k F1;
%傅里叶级数的傅里叶系数的求解公式,i是叙述单位,k是k次谐波。int函数用来求关于t1的定积分
%积分的结果应是关于k的代数式
F1=int((exp(-1i*k*pi*t1/2))/4,t1,-0.6,0.6);

%接下来对不同的k值用具体的n代替，也就是求出从-20到20次谐波的傅里叶系数的矩阵
for n=-20:20
    %之所以用求极限的方式代入数据是因为当n=0时,F1的分母为0，系统会报错
    F2=limit(F1,k,n);
    Cn=abs(F2);
    subplot(2,1,2);
    stem(n,Cn,'b','filled');%filled是实心点
    hold on;
end
xlabel('n');    
ylabel('|Cn|'); 
title("周期矩形方波 Made by Flynn")
grid on;

考虑大家可能是刚刚接触到Matlab，因此注释比较详细，大家细品肯定能够理解，日子长了大家就能区分开Matlab与其它的编程语言，并能体会到Matlab的变量处处是矩阵的魅力，这也是Matlab取名为矩阵工厂的原因，下面的例子也是大同小异，因此注释的话就没有这么详细了，大家认真研究，一定可以举一反三的。

②如果信号是冲激信号，周期不变，试绘制其幅度谱。

clear all;
t=-6:6;
xt=zeros(1,13);
xt(3)=1;xt(7)=1;xt(11)=1;
subplot(2,1,1);
stem(t,xt);
xlabel('t');ylabel('f(t)'); title('冲激串 Made by Flynn');
grid on;

syms t k;
e=exp(-1i*k*pi*t/2);
F=int(dirac(t).*e,t,-2,2)/4;
for n=-20:20
F2=limit(F,k,n);%对F2求极限
Cn=abs(F2);
subplot(2,1,2);
stem(n,Cn,'b','filled');
xlabel('n');    
ylabel('|Cn|'); 
title('冲激串幅度谱 Made by Flynn');
hold on;%画出冲激串幅度谱
end
grid on;

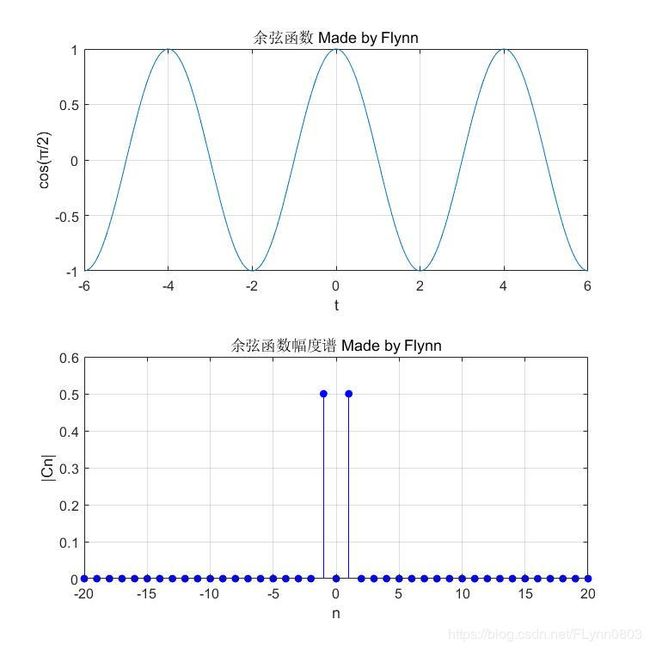
③如果信号是余弦信号，周期不变，幅度不变，初始相位为0，试绘制其幅度谱

clear all;
t=-2*pi:0.01:2*pi;
xt=cos(pi/2*t);
subplot(2,1,1);
plot(t,xt);
axis([-6 6 -1 1]);
grid on;
xlabel('t');    
ylabel('cos(π/2)'); 
title('余弦函数');%绘制余弦函数

syms t k;
f=cos(pi/2*t);
e=exp(-1i*k*pi*t/2);
F=int(f.*e,t,-2,2)/4;
for n=-20:20
F2=limit(F,k,n);% 对F2求极限
Cn=abs(F2);
subplot(2,1,2);
stem(n,Cn,'b','filled');
xlabel('n');    
ylabel('|Cn|'); 
title('余弦函数幅度谱');
hold on;%画出余弦函数幅度谱
end
grid on;

好了，本次文章就写到这里了，希望我的分享能够帮助到大家，本文或许有些纰漏之处，大家有意见也可以在下面留言，我都会一一看的，另外多说一句，实践的代码都是出于个人的理解码出来的，同一个目标有不同的实现路径，代码也不尽相同，仅供参考。