剑指Offer66题之每日6题 - 最后一天
原题链接:
- 第一题:序列化二叉树;
- 第二题:二叉搜索树的第k个结点;
- 第三题:数据流中的中位数;
- 第四题:滑动窗口的最大值;
- 第五题:矩阵中的路径;
- 第六题:机器人的运动范围;
第一题:序列化二叉树
题目:
请实现两个函数,分别用来序列化和反序列化二叉树
解析:
这个题其实很不清楚,序列化的规则是什么?题中并没有给出,而且,题中要你序列化和反序列化二叉树,从这一点可以猜到,这个题的判题规则应该是用你的规则序列出来的序列来作为反序列化的输入来的到一个新的二叉树,然后与原二叉树进行比较。
从这一点,我们可以投机取巧地通过这一题,序列化二叉树的时候返回空指针,反序列化的时候直接返回原二叉树。
/*
struct TreeNode {
int val;
struct TreeNode *left;
struct TreeNode *right;
TreeNode(int x) :
val(x), left(NULL), right(NULL) {
}
};
*/
class Solution {
public:
TreeNode *root;
char* Serialize(TreeNode *root) {
this->root = root;
return nullptr;
}
TreeNode* Deserialize(char *str) {
return root;
}
};投机取巧地做法这里就不过多讨论了,现在我们来讨论下如何定义这个序列化的规则。
规则你可以自己选择,前提是要方便你写代码,这里我说一下我的规则:
- 对于非空结点, 数字前面加一个
*,这么做的目的是区分两个靠在一起的数字,例如*18*7;- 对于空结点,用字符
#代替。- 遍历的顺序我选择了先序遍历,这里你也可以选择其余两种遍历方式。
至于反序列化,那么就根据你的规则来重建这个二叉树就好了。
具体细节,看看代码就明白了。
/*
struct TreeNode {
int val;
struct TreeNode *left;
struct TreeNode *right;
TreeNode(int x) :
val(x), left(NULL), right(NULL) {
}
};
*/
class Solution {
public:
char* Serialize(TreeNode *root) {
if (root == nullptr)
return "#";
char str[(const int)(log10(root->val) + 1 + 1 + 1)];
snprintf(str, sizeof(str), "*%d", root->val);
char *p_l = Serialize(root->left), *p_r = Serialize(root->right);
char *ret = (char *)malloc(sizeof(str) + strlen(p_l) + strlen(p_r));
ret[0] = 0;
strncat(ret, str, strlen(str));
strncat(ret, p_l, strlen(p_l));
strncat(ret, p_r, strlen(p_r));
return ret;
}
TreeNode* Deserialize(char *str) {
return _Deserialize(&str);
}
private:
TreeNode* _Deserialize(char **str) {
if (!(*str)[0])
return nullptr;
if ((*str)[0] == '#')
return (*str)++, nullptr;
char *p1 = strstr((*str) + 1, "*"),
*p2 = strstr((*str) + 1, "#"), *p = nullptr;
if (p1 == nullptr && p2 == nullptr)
p = strlen(*str) + *str;
else if (p1 != nullptr && p2 != nullptr)
p = p1 > p2 ? p2 : p1;
else
p = p1 == nullptr ? p2 : p1;
char digit[(const int)(p - (*str))];
strncpy(digit, (*str) + 1, p - (*str) - 1);
TreeNode *ret = new TreeNode(atoi(digit));
*str = p;
ret->left = _Deserialize(str);
ret->right = _Deserialize(str);
return ret;
}
};第二题:二叉搜索树的第k个结点
题目:
给定一颗二叉搜索树,请找出其中的第k大的结点。例如
5
/ \
3 7
/\ /\
2 4 6 8
按结点数值大小顺序第三个结点的值为4。
如何得到一个数据流中的中位数?如果从数据流中读出奇数个数值,那么中位数就是所有数值排序之后位于中间的数值。如果从数据流中读出偶数个数值,那么中位数就是所有数值排序之后中间两个数的平均值。
解析:
两种方法,第一种就是设置一个访问次序变量,访问第一个变量的时候该次序变量为一,以后顺序每访问一个变量就让该次序变量自增,直到等于
k。
/*
struct TreeNode {
int val;
struct TreeNode *left;
struct TreeNode *right;
TreeNode(int x) :
val(x), left(NULL), right(NULL) {
}
};
*/
class Solution {
public:
TreeNode* KthNode(TreeNode* pRoot, int k)
{
return dfs(pRoot, k, k = 0);
}
TreeNode *dfs(TreeNode *pRoot, int k, int &c)
{
if (!k || pRoot == nullptr)
return nullptr;
TreeNode *ret = dfs(pRoot->left, k, c);
if (ret == nullptr)
return ++c == k ? pRoot : dfs(pRoot->right, k, c);
return ret;
}
};
第二种方法是,统计出左右子树结点的个数,类似于剑指Offer66题之每日6题 - 第五天中第五题中的快排解法,统计个数使用了指针,这个类似于剑指Offer66题之每日6题 - 第七天中第三题中的第二种解法,这样每个结点只访问了一次。
/*
struct TreeNode {
int val;
struct TreeNode *left;
struct TreeNode *right;
TreeNode(int x) :
val(x), left(NULL), right(NULL) {
}
};
*/
class Solution {
public:
TreeNode* KthNode(TreeNode* pRoot, int k)
{
return k ? dfs(pRoot, k, &k) : nullptr;
}
TreeNode *dfs(TreeNode *pRoot, int k, int *p)
{
if (pRoot == nullptr)
return *p = 0, nullptr;
int n_l, n_r;
TreeNode *ret = nullptr;
if ((ret = dfs(pRoot->left, k, &n_l)) == nullptr)
return k - n_l == 1 ? pRoot :
(ret = dfs(pRoot->right, k - n_l - 1, &n_r), *p = 1 + n_r + n_l, ret);
return ret;
}
};第三题:数据流中的中位数
题目:
如何得到一个数据流中的中位数?如果从数据流中读出奇数个数值,那么中位数就是所有数值排序之后位于中间的数值。如果从数据流中读出偶数个数值,那么中位数就是所有数值排序之后中间两个数的平均值。
解析:
第一种做法是维护一个排好序的序列,那么求中位数就可以利用下标直接算出来,插入数据的时候使用插入排序的方法插入。
class Solution {
private:
vector<int> arr;
public:
void Insert(int num)
{
arr.push_back(num);
for (int i = (int)arr.size() - 1; i >= 1 && arr[i] < arr[i - 1]; swap(arr[i], arr[i - 1]), i--);
}
double GetMedian()
{
return (arr[((int)arr.size() - 1) / 2] + arr[arr.size() / 2]) / 2.0;
}
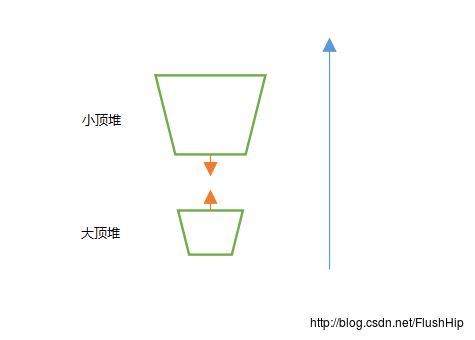
};第二种做法是维护一个大顶堆和一个小顶堆,两个堆中的元素数量之差保持在小于等于1(小顶堆中的元素永远不小于大顶堆中的元素数量),同时还要保证大顶堆中的所有元素都小于小顶堆中的元素(代码中的
ope函数就是保证这一点的),这样查询的时候可以取出大小堆的堆顶元素进行操作,从而得到答案。
下图可以直观看出这种方法的思想:
class Solution {
private:
priority_queue<int, vector<int>, less<int> > litte;
priority_queue<int, vector<int>, greater<int> > big;
void ope()
{
if (big.empty())
return ;
auto l = litte.top(), b = big.top();
if (l > b) {
litte.pop();
big.pop();
litte.push(b);
big.push(l);
}
}
public:
void Insert(int num)
{
litte.size() == big.size() ? litte.push(num) : big.push(num);
ope();
}
double GetMedian()
{
return litte.size() == big.size() ? (litte.top() + big.top() + 0.0) / 2 : litte.top();
}
};第四题:滑动窗口的最大值
题目:
给定一个数组和滑动窗口的大小,找出所有滑动窗口里数值的最大值。例如,如果输入数组
{2,3,4,2,6,2,5,1}及滑动窗口的大小3,那么一共存在6个滑动窗口,他们的最大值分别为{4,4,6,6,6,5}; 针对数组{2,3,4,2,6,2,5,1}的滑动窗口有以下6个:{[2,3,4],2,6,2,5,1}, {2,[3,4,2],6,2,5,1}, {2,3,[4,2,6],2,5,1}, {2,3,4,[2,6,2],5,1}, {2,3,4,2,[6,2,5],1}, {2,3,4,2,6,[2,5,1]}。
解析:
单调队列是最佳的做法。
那么什么是单调队列呢,简单说一下单调队列:如果你知道单调栈的话,那么单调队列很好理解, 单调队列的目的就是去除冗余的信息,留下那些有用的信息,举个例子,输入数组
{2, 3, 4, 1, -1, -2},滑动窗口大小是3,那么2如队列;3入队列前,发现队尾元素为2,于是弹出2,3入队;4入队前发现队尾元素是3,于是弹出3,4入队;1入队;-1入队;-2入队。以上就是单调队列的操作过程,这里求的是固定区间长度的最大值,那么单调队列始终保持队头元素最大,队内元素依次递减,故要得到一个某一个固定长度的区间的最大值,直接取出队头元素即可。
单调队列和下面这个例子比较像:现在有张三,李四,王五三个人竞选一个职位,只有三个候选人且如果一个人当选过候选人但是又被踢走,那么这个人再也不能当候选人了。张三的能力值为2,李四的能力值为9, 王五的能力值为6,那么这三个人都以当候选人,当然,有李四在,张三永远选不上,所以张三就是一个多余的人(冗余信息),故把张三排除掉;那么王五可不可能选上呢?王五是可能的,如果李四走掉了,那么王五就选上了,因此王五就是第二候选人,这个时候,来了一个王麻子,能力值为80,候选人分别为李四,王五,王麻子发现李四,王五的能力太差,他自己说:“有我王麻子在,李四,王五永远不可能坐上这个位置!”,于是候选人现在就只剩王麻子了。例子可能不是很好,但是对理解单调队列还是很直观的。
由于要从队尾弹出元素,故数据结构要选择双端队列
deque。如果对单调队列还不理解,可以参考网上的其余博客。最后说一句,单调队列求的是固定区间长度中的最大最小值,单调栈求的是以当前元素为最大最小值的最大区间范围。
class Solution {
public:
vector<int> maxInWindows(const vector<int>& num, unsigned int size)
{
vector<int> ret;
deque<int> que;
for (unsigned int i = 0; i < num.size(); i++) {
if (!que.empty() && i - que.front() == size)
que.pop_front();
for (; !que.empty() && num[que.back()] < num[i]; que.pop_back()) {}
que.push_back(i);
if (i >= size - 1)
ret.push_back(num[que.front()]);
}
return ret;
}
};第五题:矩阵中的路径
题目:
请设计一个函数,用来判断在一个矩阵中是否存在一条包含某字符串所有字符的路径。路径可以从矩阵中的任意一个格子开始,每一步可以在矩阵中向左,向右,向上,向下移动一个格子。如果一条路径经过了矩阵中的某一个格子,则该路径不能再进入该格子。 例如
a b c e s f c s a d e e矩阵中包含一条字符串"bcced"的路径,但是矩阵中不包含"abcb"路径,因为字符串的第一个字符b占据了矩阵中的第一行第二个格子之后,路径不能再次进入该格子。
解析:
dfs d f s ,普通的深搜,不多解释。
class Solution {
public:
bool hasPath(char* matrix, int rows, int cols, char* str)
{
int i;
bool used[(const int)strlen(matrix)];
for (memset(used, false, sizeof(used)),
i = 0; matrix[i] && !dfs(matrix, rows, cols, i / cols, i % cols, str, used);
memset(used, false, sizeof(used)), i++);
return matrix[i];
}
bool dfs(char *matrix, int rows, int cols, int x, int y, char *ptr, bool used[])
{
if (ptr[0] == 0)
return true;
if (!(x >= 0 && x < rows && y >= 0 && y < cols && !used[x * cols + y] && matrix[x * cols + y] == ptr[0]))
return false;
used[x * cols + y] = true;
int dirx[] = {0, 0, 1, -1}, diry[] = {1, -1, 0, 0}, k;
for (k = 0; k < 4 && !dfs(matrix, rows, cols, x + dirx[k], y + diry[k], ptr + 1, used); k++);
return used[x * cols + y] = false, k != 4;
}
};第六题:机器人的运动范围
题目:
地上有一个
m行和n列的方格。一个机器人从坐标(0,0)的格子开始移动,每一次只能向左,右,上,下四个方向移动一格,但是不能进入行坐标和列坐标的数位之和大于k的格子。 例如,当k为18时,机器人能够进入方格(35,37),因为3+5+3+7 = 18。但是,它不能进入方格(35,38),因为3+5+3+8 = 19。请问该机器人能够达到多少个格子?
解析:
bfs b f s ,普通的广搜,不多解释。
class Solution {
public:
int getSum(int x) {
int ret = 0;
for (; x; ret += x % 10, x /= 10);
return ret;
}
int movingCount(int threshold, int rows, int cols)
{
const int dirx[] = {0, 0, 1, -1};
const int diry[] = {1, -1, 0, 0};
queue<int> que;
vector<bool> used(rows * cols, false);
que.push(0 * cols + 0);
used[0 * cols + 0] = true;
int ret = 0;
while (!que.empty()) {
auto now = que.front();
que.pop();
if (getSum(now / cols) + getSum(now % cols) <= threshold)
ret++;
else
continue;
for (int i = 0; i < 4; i++) {
int tx = now / cols + dirx[i],
ty = now % cols + diry[i];
if (tx >= 0 && tx < rows && ty >= 0 && ty < cols &&
!used[tx * cols + ty]) {
used[tx * cols + ty] = true;
que.push(tx * cols + ty);
}
}
}
return ret;
}
};