奇异值分解SVD
奇异值是矩阵里的概念,一般通过奇异值分解定理求得。
奇异值分解是一个有着很明显的物理意义的一种方法,它可以将一个比较复杂的矩阵用更小更简单的几个子矩阵的相乘来表示,这些小矩阵描述的是矩阵的重要的特性。就像是描述一个人一样,给别人描述说这个人长得浓眉大眼,方脸,络腮胡,而且带个黑框的眼镜,这样寥寥的几个特征,就让别人脑海里面就有一个较为清楚的认识,实际上,人脸上的特征是有着无数种的,之所以能这么描述,是因为人天生就有着非常好的抽取重要特征的能力,让机器学会抽取重要的特征,SVD是也一个重要的方法。在机器学习领域,有相当多的应用与奇异值都可以扯上关系,比如做feature reduction的PCA,做数据压缩(以图像压缩为代表)的算法,还有做搜索引擎语义层次检索的LSI(Latent Semantic Indexing),还有推荐系统中也有用到SVD的基于协同过滤的方法。
关于SVD和PCA的区别和联系,请见降维方法PCA与SVD的联系与区别
特征值分解(EVD)
首先回顾下特征值和特征向量的定义如下:
A q i = λ i q i , q i T q j = 0 ( i ≠ j ) A q_{i}=\lambda_{i} q_{i}, \quad q_{i}^{T} q_{j}=0(i \neq j) Aqi=λiqi,qiTqj=0(i=j)
其中 A A A 是一个 n × n n \times n n×n 矩阵, q q q 是一个 n n n 维向量,则 λ \lambda λ 是矩阵 A A A 的一个特征值,而 q q q 是矩阵 A A A 的特征值 λ \lambda λ 所对应的特征向量。
特征值分解,如果矩阵 A A A 是一个的实对称矩阵(即 A = A T A=A^T A=AT),那么它可以被分解成如下的形式:
A = Q Λ Q T = Q [ λ 1 ⋯ ⋯ ⋯ ⋯ λ 2 ⋯ ⋯ ⋯ ⋯ ⋱ ⋯ ⋯ ⋯ ⋯ λ m ] Q T (1) A = Q\Lambda Q^T= Q\left[ \begin{matrix} \lambda_1 & \cdots & \cdots & \cdots\\ \cdots & \lambda_2 & \cdots & \cdots\\ \cdots & \cdots & \ddots & \cdots\\ \cdots & \cdots & \cdots & \lambda_m\\ \end{matrix} \right]Q^T \tag{1} A=QΛQT=Q⎣⎢⎢⎡λ1⋯⋯⋯⋯λ2⋯⋯⋯⋯⋱⋯⋯⋯⋯λm⎦⎥⎥⎤QT(1)
其中 Q Q Q 为标准正交阵,即,特征向量 q i ∈ Q q_i \in Q qi∈Q 标准化,有 Q Q T = E QQ^T=E QQT=E ,或者 Q T Q = E Q^TQ=E QTQ=E,或者 Q T = Q − 1 Q^T=Q^{-1} QT=Q−1, Λ \Lambda Λ 为对角矩阵,且上面的矩阵的维度均为 n × n n \times n n×n。 λ i ∈ Λ \lambda_i \in \Lambda λi∈Λ 称为特征值, q i ∈ Q q_i \in Q qi∈Q 是(特征矩阵)中的列向量。
那么如果 A A A 不是方阵,即行和列不相同时,我们还可以对矩阵进行分解吗?答案是可以,此时我们的SVD登场了.
奇异值分解(SVD)
奇异值定义
有一个 m × n m \times n m×n 的实数矩阵 A A A,我们想要把它分解成如下的形式:
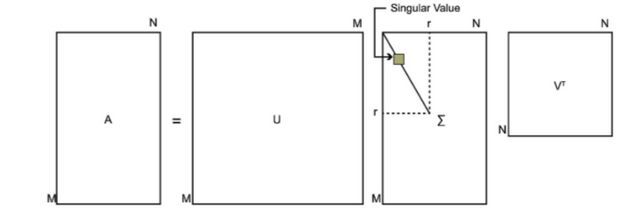
A = U Σ V T ( 2 ) A=U\Sigma V^T(2) A=UΣVT(2)
其中 U U U 和 V V V 均为单位正交阵,即有 U U T = E U U^{T}=E UUT=E 和 V V T = E V V^{T}=E VVT=E , U U U 称为左奇异矩阵, V V V 称为右奇异矩阵, Σ \Sigma Σ 仅在主对角线上有值,我们称它为奇异值,其它元素均为0,矩阵 A A A 分解过程就叫SVD。上面矩阵的维度分别为 U ∈ R m × m , Σ ∈ R m × n , V ∈ R n × n U \in R^{m \times m}, \Sigma \in R^{m \times n}, V \in R^{n \times n} U∈Rm×m,Σ∈Rm×n,V∈Rn×n 。通常,主对角线上的奇异值从大到小排列。
一般地, Σ \Sigma Σ 有如下形式:
Σ = [ σ 1 0 0 0 0 0 σ 2 0 0 0 0 0 ⋱ 0 0 0 0 0 ⋱ 0 ] m × n \Sigma = \left[ \begin{matrix} \sigma_1 & 0 & 0 & 0 & 0\\ 0 & \sigma_2 & 0 & 0 & 0\\ 0 & 0 & \ddots & 0 & 0\\ 0 & 0 & 0 & \ddots & 0\\ \end{matrix} \right]_{m\times n} Σ=⎣⎢⎢⎡σ10000σ20000⋱0000⋱0000⎦⎥⎥⎤m×n
下图可以很形象的看出上面SVD的定义:
奇异值求解
如果我们将 A A A 和 A A A 的转置做矩阵乘法,那么会得到 n × n n×n n×n 的一个方阵 A A T A A^{T} AAT 。既然 A A T A A^{T} AAT 是方阵,那么我们就可以进行特征分解,得到的特征值和特征向量满足下式:
( A A T ) u i = λ i u i \left(A A^{T}\right) u_{i}=\lambda_{i} u_{i} (AAT)ui=λiui
这样我们就可以得到矩阵 A A T A A^{T} AAT 的 m m m 个特征值和对应的 m m m 个特征向量 u u u 了。将 A A T A A^{T} AAT 的所有特征向量张成一个 m × m m \times m m×m 的矩阵 U U U ,就是我们SVD公式里面的 U U U 矩阵了。一般我们将 U U U 中的每个特征向量叫做 A A A 的左奇异向量。
同理,如果我们将 A A A 的转置和 A A A 做矩阵乘法,那么会得到 m × m m×m m×m 的一个方阵 A T A A^{T} A ATA ,得到的特征值和特征向量满足下式:
( A T A ) v i = λ i v i \left(A^{T} A\right) v_{i}=\lambda_{i} v_{i} (ATA)vi=λivi
这样我们就可以得到矩阵 A T A A^{T} A ATA 的 n n n 个特征值和对应的 n n n 个特征向量 v v v 了。将 A T A A^{T} A ATA 的所有特征向量张成一个 n × n n×n n×n 的矩阵 V V V,就是我们SVD公式里面的 V V V 矩阵了。一般我们将 V V V 中的每个特征向量叫做 A A A 的右奇异向量。
如果我们将 A = U Σ V T A=U\Sigma V^T A=UΣVT 代入 A A T A A^{T} AAT ,有:
A A T = U Σ V T V Σ T U T = U Σ Σ T U T ( 3 ) A A^{T}=U \Sigma V^{T} V \Sigma^{T} U^{T}=U \Sigma \Sigma^{T} U^{T}(3) AAT=UΣVTVΣTUT=UΣΣTUT(3)
同理,带入 A T A A^{T} A ATA ,有:
A T A = V Σ T U T U Σ V T = V Σ T Σ V T ( 4 ) A^{T} A=V \Sigma^{T} U^{T} U \Sigma V^{T}=V \Sigma^{T} \Sigma V^{T}(4) ATA=VΣTUTUΣVT=VΣTΣVT(4)
注: Σ Σ T \Sigma \Sigma ^T ΣΣT 与 Σ T Σ \Sigma ^T\Sigma ΣTΣ 在矩阵的角度上来讲,它们是不相等的,因为它们的维数不同, Σ Σ T ∈ R m × m \Sigma \Sigma ^T\in R^{m\times m} ΣΣT∈Rm×m, 而 Σ T Σ ∈ R n × n \Sigma ^T \Sigma \in R^{n\times n} ΣTΣ∈Rn×n,但是它们在主对角线的奇异值是相等的,即有:
Σ Σ T = [ σ 1 2 0 0 0 0 σ 2 2 0 0 0 0 ⋱ 0 0 0 0 ⋱ ] m × m \Sigma \Sigma^{T}=\left[\begin{array}{cccc} {\sigma_{1}^{2}} & {0} & {0} & {0} \\ {0} & {\sigma_{2}^{2}} & {0} & {0} \\ {0} & {0} & {\ddots} & {0} \\ {0} & {0} & {0} & {\ddots} \end{array}\right]_{m \times m} ΣΣT=⎣⎢⎢⎡σ120000σ220000⋱0000⋱⎦⎥⎥⎤m×m
Σ T Σ = [ σ 1 2 0 0 0 0 σ 2 2 0 0 0 0 ⋱ 0 0 0 0 ⋱ ] n × n \Sigma^{T} \Sigma=\left[\begin{array}{cccc} {\sigma_{1}^{2}} & {0} & {0} & {0} \\ {0} & {\sigma_{2}^{2}} & {0} & {0} \\ {0} & {0} & {\ddots} & {0} \\ {0} & {0} & {0} & {\ddots} \end{array}\right]_{n \times n} ΣTΣ=⎣⎢⎢⎡σ120000σ220000⋱0000⋱⎦⎥⎥⎤n×n
可以看到式(3)与式(1)的形式非常相似,同时也是对称矩阵,即可以利用式(1),做特征值分解。利用式(3)特征值分解,得到的特征矩阵即为 V V V;利用式(4)特征值分解,得到的特征矩阵即为 V V V;对 Σ Σ T \Sigma \Sigma ^T ΣΣT 或 Σ T Σ \Sigma ^T\Sigma ΣTΣ 中的特征值开方,可以得到所有的奇异值。
假设我们现在有矩阵
A = [ 1 5 7 6 1 2 1 10 4 4 3 6 7 5 2 ] A=\left[\begin{array}{lllll} {1} & {5} & {7} & {6} & {1} \\ {2} & {1} & {10} & {4} & {4} \\ {3} & {6} & {7} & {5} & {2} \end{array}\right] A=⎣⎡1235167107645142⎦⎤
需要对其做奇异值分解,那么可以求出 A A T AA^T AAT 和 A T A A^TA ATA,如下:
A A T = [ 112 105 114 105 137 110 114 110 123 ] A A^{T}=\left[\begin{array}{ccc} {112} & {105} & {114} \\ {105} & {137} & {110} \\ {114} & {110} & {123} \end{array}\right] AAT=⎣⎡112105114105137110114110123⎦⎤
A T A = [ 14 25 48 29 15 25 62 87 64 21 48 87 198 117 61 29 64 117 77 32 15 21 61 32 21 ] A^{T} A=\left[\begin{array}{ccccc} {14} & {25} & {48} & {29} & {15} \\ {25} & {62} & {87} & {64} & {21} \\ {48} & {87} & {198} & {117} & {61} \\ {29} & {64} & {117} & {77} & {32} \\ {15} & {21} & {61} & {32} & {21} \end{array}\right] ATA=⎣⎢⎢⎢⎢⎡14254829152562876421488719811761296411777321521613221⎦⎥⎥⎥⎥⎤
分别对上面做特征值分解,得到如下结果:
U =
[[-0.55572489, -0.72577856, 0.40548161],
[-0.59283199, 0.00401031, -0.80531618],
[-0.58285511, 0.68791671, 0.43249337]]
V =
[[-0.18828164, -0.01844501, 0.73354812, 0.65257661, 0.06782815],
[-0.37055755, -0.76254787, 0.27392013, -0.43299171, -0.17061957],
[-0.74981208, 0.4369731 , -0.12258381, -0.05435401, -0.48119142],
[-0.46504304, -0.27450785, -0.48996859, 0.39500307, 0.58837805],
[-0.22080294, 0.38971845, 0.36301365, -0.47715843, 0.62334131]]
Σ = Diag ( 18.54 , 1.83 , 5.01 ) \Sigma=\operatorname{Diag}(18.54,1.83,5.01) Σ=Diag(18.54,1.83,5.01)
总结
奇异值可以被看作成一个矩阵的代表值,或者说,奇异值能够代表这个矩阵的信息。当奇异值越大时,它代表的信息越多。因此,我们取前面若干个最大的奇异值,就可以基本上还原出数据本身。
SVD作为一个很基本的算法,在很多机器学习算法中都有它的身影,特别是在现在的大数据时代,由于SVD可以实现并行化,因此更是大展身手。
SVD的缺点是分解出的矩阵解释性往往不强,有点黑盒子的味道,不过这不影响它的使用。
推荐阅读:
奇异值分解(SVD)
SVD(奇异值分解)小结
奇异值分解(SVD)详解及其应用
漫谈奇异值分解
降维方法PCA与SVD的联系与区别