基于DNN的推荐算法
本文为《推荐系统与深度学习》第六章的复习笔记,只记录了一些要点,希望能够快速的进行复习,如果发现哪一个点不明白的话,可以自行展开学习或者加小编微信进行沟通。
深度学习在推荐中发挥的作用:
- 能够直接从内容中提取特征,表征能力强
- 容易对噪声数据进行处理,抗噪能力强
- 可以使用循环神经网络对动态或者序列数据进行建模
- 可以更加准确的学习user和item的特征
基于DNN的推荐算法
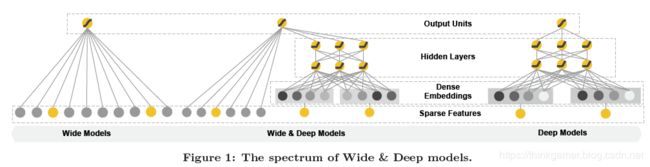
推荐系统和通用搜索排序问题共有的一大挑战为同时具备记忆能力和泛化能力。
- 记忆能力可以解释为学习那些经常共同出现的特征,发现历史数据中存在的共现性(提升推荐的准确性)
- 泛化能力则基于迁移相关性,探索之前几乎没有出现过的新特征组合(提升推荐的多样性)
比如 YouTube 2006年提出的Wide & Deep模型
整个推荐系统可分为召回和排序两个阶段,召回阶段一般通过i2i/u2i/u2u/user profile等方式“粗糙”地召回候选物品,召回阶段的数量是百万级别的,排序阶段则是对召回阶段的数据使用更精细的特征进行计算user-item的排序分,作为最终输出推荐结果的依据。
召回阶段
把推荐问题建模成一个“超大规模多分类”问题,即在时刻 t t t,为用户 U U U(上下文信息 C C C)在视频库 V V V中精准地预测出视频 i i i的类别(每个具体的视频视为一个类别, i i i即为一个类别),用数学公式表达如下:
P ( w t = i ∣ U , C ) = e v i , u ∑ j ∈ V e v i , u P(w_t=i|U,C)=\frac{e^{v_i,u}}{\sum_{j \in V} e^{v_i,u}} P(wt=i∣U,C)=∑j∈Vevi,uevi,u
上式为一个softmax多分类器,向量 u ∈ R N u \in R^N u∈RN是 < u s e r , c o n t e x t >
在这种超大规模分类问题上,至少要有几百万个类别,实际训练采用的是Negative Sample(负采样),或是word2vec方法中提到的SkipGram方法。
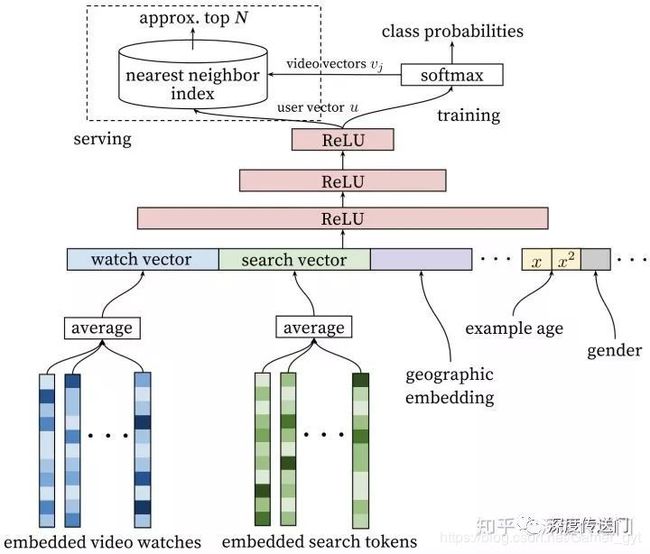
整个模型包含三个隐含的DNN结构,如下图所示。输入是用户浏览历史、搜索历史、人口统计学信息和其余上下文信息concat成的输入向量,输出分为线上和离线训练两个部分。
离线训练阶段输出层为softmax层,输出为上述公式表达的概率。线上则是直接利用user向量查询相关商品,最重要问题在性能方面,则利用类似局部敏感哈希的算法提供最相关的 N N N个视频。
类似于word2vec算法,每个视频都会被embedding到固定维度的向量中,用户不同行为下的视频,通过加权平均等方式汇总得到固定维度的vector作为DNN输入。
特征一般从下面几个方面入手:
- 用户有行为的物品(点击、点赞、收藏、关注、分享、评论等,不同地方行为定义可能会有不同),将其进行embedding
- 人口统计学信息:性别、年龄、地域等
- 其他上下文信息:设备、登陆状态、时间等
- 交叉信息:用户xCate(cate可以是物品的类别、属性等)
在有监督学习问题中,最重要的是选择Label(目标变量),因为label决定了模型的训练目标,而模型和特征是为了逼近label。
训练模型时的小trick:
- 使用更广的数据源,即不局限于推荐场景的数据,也可以包括搜索等的数据
- 为每个用户生成固定数量的训练样本,即平等的对待每一个用户,避免loss被少数活跃用户代表,能明显提升线上效果
- 抛弃序列信息,即对过去用户有行为的query的embedding向量进行加权平均
- 不对称的共同浏览(asymmetric cowatch)问题:所谓的asymmetric cowatch指的是用户在浏览视频时候,往往都是序列式的,开始看一些比较流行的,逐渐找到细分的领域
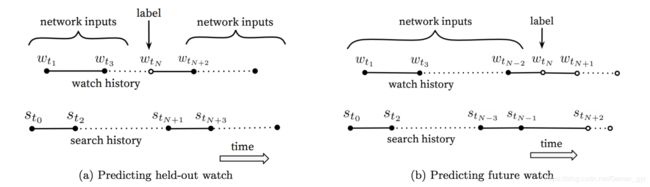
下图(a)是heldout方式,利用上下文信息预估中间的一个视频,图(b)是predicting next watch的方式,则是利用上文信息,预估下一次浏览的视频。实验结果表示tu(b)的方式在线上A/B Test 中表现更佳,实际上,传统的协同过滤算法,都是隐含地采用图(a)的heldout方式,忽略了不对称的浏览模型。
排序阶段
在指定rank label的时候,单纯的CTR是有迷惑性的,比如某些靠关键词或者图片吸引用户进行高点击的视频、文章的跳出率是很高的,因此设定label的时候要与自己想要得到的期望KPI相一致(比如留存、时长等),同时通过线上的A/B Test进行调整。
特征工程中最难的是如何建模用户时序行为(temporal sequence of user actions),并且将这些行为和要排序的item进行关联。
下面列出来一些特征工程的小trick:
- 考虑用户在类别下的行为汇总,比如度量用户对视频的喜欢程度,可以考虑用户与视频在所在频道间的关系
- 数量特征(浏览某个类别的次数)和时间特征(最近一次浏览某个类别距今时间),这两类特征具有很强的泛化能力。除了这两类正向的特征,用户在某些类别的PV但不点击的行为,即负反馈sigmal同样非常重要
- 把召回阶段的信息(比如推荐的来源和所在的来源分数),传播到排序阶段也同样能够取得很好的提升效果
- 用NN处理连续特征,将稀疏的高基数空间的离散特征embedding到稠密的向量中(维度的选定一般遵循log法,假设有100维的无重复特征,可以embedding到10维)
- ID编码类特征并不需要对全部的id进行embedding编码,只需要对top N的物品进行embedding编码即可,其余置为0
- 同维度不同特征采用的相同ID的embedding是共享的(比如过去浏览的物品ID,点击的物品ID),这样可以大大加速训练过程,但要注意的是输入层要进行分别填充
- NN对输入特征的尺度和分布都是非常敏感的,基本除了树模型,大多数ML算法都是这样,一般会对特征进行归一化处理,加速模型收敛过程,一种推荐的归一化方法为:累计分位点, x ˉ = ∫ − ∞ x d f \bar{x} = \int_{-\infty }^{x} df xˉ=∫−∞xdf
- 特征构造时会讲归一化后的 x ˉ \bar{x} xˉ的平方根 x ˉ \sqrt{\bar{x}} xˉ和平方 x ˉ 2 \bar{x}^2 xˉ2作为网络输入,以期望网络更容易的学到特征的次线性(sub-linear)和超线性(super-linear)函数
基于DeepFM的推荐算法
DeepFm的设计思路来自于哈工大&华为诺亚方舟实验室,主要关注如何学习user behavior背后的组合特征(feature interactions),从而最大化推荐系统的CTR,论文提出构建一个端到端的可以同时突出低阶和高阶feature interactions的学习模型DeepFM
DeepFM由FM和NN组成,和Wide & Deep的结构类似,但弥补了W&D的一些不足,LR是TR中最常用的算法,但LR的前提是假设特征之间是相互独立的,没有考虑特征之间的相互关系,即忽略了feature pair等高阶信息。比如在某个场景下,男性和女性的点击率是不一样的,如果是LR这回分别考虑性别和点击次数两个特征,这显然是不合适的,当然也可以通过特征交叉解决这种情况,但是依赖强大的特征工程工作。
LR加上特征交叉,模型中的 θ ( x ) \theta(x) θ(x)表示为(公式-1):
θ ( x ) = w 0 = ∑ i = 1 n w i x i + ∑ i = 1 n − 1 ∑ j = i + 1 n w i j x i x j \theta(x) = w_0 = \sum_{i=1}^{n}w_ix_i + \sum_{i=1}^{n-1} \sum_{j=i+1}^{n} w_{ij}x_ix_j θ(x)=w0=i=1∑nwixi+i=1∑n−1j=i+1∑nwijxixj
其中 w i j w_{ij} wij是 f e a t u r e p a i r < x i , y j > feature \,pair
- 参数空间大幅度增加,由线性增加至平方级
- 样本比较稀疏
因此需要寻找一种方法将其进行分解,即FM算法
FM
FM(Factorization Machine)主要是为了解决数据稀疏的情况下特征怎样组合的问题,另外我们通常所说的FM算法为二元的FM。
FM算法把公式-1中的 w i j w_{ij} wij拆分成两个向量 < v i , v j >
θ ( x ) = w 0 = ∑ i = 1 n w i x i + ∑ i = 1 n − 1 ∑ j = i + 1 n < v i , v j > x i x j \theta(x) = w_0 = \sum_{i=1}^{n}w_ix_i + \sum_{i=1}^{n-1} \sum_{j=i+1}^{n}
直观来看,FM认为当一个特征 w i w_i wi需要与其他特征 w j w_j wj考虑组合线性的时候,只需要一组 k k k维向量 v i v_i vi即可代表 x i x_i xi,而不需针对所有特征分别计算出不同的组合参数 w i j w_{ij} wij,这相当于将特征映射到一个 k k k维空间,用向量关系表示特征关系。这与矩阵分解的思想是类似的。
比如在协同过滤中,一个rating矩阵,可以分解为user矩阵和item矩阵,每个user和item都可以采用一个隐向量表示。比如在下图中的例子中,我们把每个user表示成一个二维向量,同时把每个item表示成一个二维向量,两个向量的点积就是矩阵中user对item的打分。
所有的二次项参数 w i j w_{ij} wij可以组成一个对称矩阵 W W W,那么这个矩阵可以分解为 W = V T ∗ V W=V^T * V W=VT∗V, V V V的第 j j j列便是第 j j j维特征的隐向量,换句话说就是每个参数 w i j = < v i , v j > w_{ij}=
假设隐向量的长度为 K K K,这样公式-1中的模型参数就从 n 2 n^2 n2降到了 n k nk nk,远远小于多项式模型的参数数量。
FM的优点:
- 降低了交叉项参数学习不充分的影响
- 提高模型的预估能力
- 提升参数的学习效率
一句话总结就是:FM模型对稀疏数据有更好的学习能力,通过交互项可以学习特征之间的关联关系,并且保证了学习效率和预估能力
DeepFM
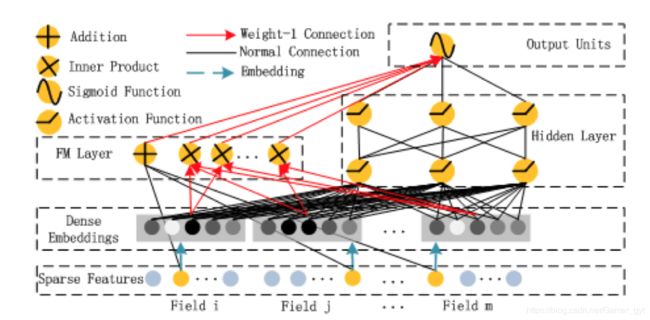
上图为DeepFM的网络结构图,从图中可以看出,左侧部分是一个FM算法,右侧则是NN,他具有以下特点:
- 结合了广度和深度模型的优点,联合训练FM模型和DNN模型,同时学习低阶特征组合和高阶特征组合
- 端到端模型,无需特征工程
- DeepFM 共享相同的输入和 embedding vector,训练更高效
- 评估模型时,用到了一个新的指标“Gini Normalization”
上图中在FM和DNN之前引入了一层Dense Embedding层,其目的是对输入向量进行“压缩”,降低模型训练的特征维度。
有几点需要注意的:
- Sparse Featurs表示原始的经过onehot处理的特征
- Dense Embeddings为FM算法中的特征交叉项的隐向量矩阵铺平,Dense Embeddings的维度由field的个数和隐向量的长度相乘决定
- Sparse Features层和Dense Embeddings层进行特征交叉计算即为FM算法的特征交叉计算项
- 特征交叉项的隐向量矩阵铺平之后在FM和DNN之间是共享的
- Field i表示的是i特征,但是i特征经过编码之后可能会有多维,比如性别特征,onehot编码后为男、女、未知
更多关于DeepFM可以参考:
- 原始论文:https://arxiv.org/abs/1703.04247
- https://www.cnblogs.com/wkang/p/9881921.html
- https://zhuanlan.zhihu.com/p/41439552
基于矩阵分解和图像特征的推荐算法
近些年基于上下文环境的推荐系统引起了大家的广泛关注,这些上下文环境包括物品的属性、用户画像特征、物品的评论等。研究人员希望通过这些附加信息来缓解评分数据稀疏等问题,对于那些没有评分数据的物品,可以基于上下文环境来推荐,从而进一步提升推荐系统的质量。
图像在一定程度上也能表达物品的内容属性信息,比如两部电影的色调、布局等,因此如果将电影的图像信息也加到推荐系统中,必定能提升推荐系统的效果。为此,作者们提出了一种基于矩阵分解和图像特征的推荐算法(Matrix Factorization+,缩写为MF+)。
假设有用户和电影的偏好矩阵 X ∈ R m ∗ n X \in R^{m*n} X∈Rm∗n,其中 m m m代表用户的数量, n n n代表电影的数量,矩阵 X X X里的每个元素 x u v x_{uv} xuv代表用户 u u u对物品 v v v的偏好。如果加入图像特征,则用户 u u u对电影 v v v的偏好 x ^ u v \hat{x}_{uv} x^uv可以表示为:
x ^ u v = μ + b u + b v + U ∗ u T ( V ∗ v + η ) \hat{x}_{uv} = \mu + b_u + b_v + U^T_{*u}(V_{*v} + \eta ) x^uv=μ+bu+bv+U∗uT(V∗v+η)
其中:
- U ∗ u U_{*u} U∗u表示用户 u u u的偏好向量
- V ∗ v V_{*v} V∗v是电影 v v v的偏好向量
- μ \mu μ是总评分的偏置项
- b u b_u bu 表示用户 u u u的偏置项
- b v b_v bv 表示电影 v v v的偏置项
- η \eta η 表示电影的视觉特征,可以写为:
η = ∣ ∣ N ( θ , v ) ∣ ∣ − 1 2 ∑ s ∈ N ( θ , v ) θ s v χ ^ s ϕ ( v ) \eta = \frac { ||N(\theta,v)||^{-\frac{1}{2}} \sum_{s\in N(\theta,v)} \theta_{sv} \hat{\chi }_s }{ \phi (v) } η=ϕ(v)∣∣N(θ,v)∣∣−21∑s∈N(θ,v)θsvχ^s
其中:
- θ s v \theta_{sv} θsv 表示电影 v v v 和 s s s的相似度
- N ( θ , v ) N(\theta,v) N(θ,v) 表示相似度大于 θ \theta θ的电影集合
- ϕ ( v ) \phi (v) ϕ(v) 是缩放因子,表示海报和静止帧图片的一致性
- $\hat{\chi }_s $ 表示海报和多张静止图片的集合
扫一扫 关注微信公众号!号主 专注于搜索和推荐系统,尝试使用算法去更好的服务于用户,包括但不局限于机器学习,深度学习,强化学习,自然语言理解,知识图谱,还不定时分享技术,资料,思考等文章!