机器学习常用可视化系列(一)

概述

在做机器学习的过程中，可视化能帮助我们了解模型训练状态，评估模型效果，还能了解数据，帮助我们了解算法模型，改善模型，在论文中好的可视化也是大大加分的~下面我总结了一下我在做机器学习时候常用的可视化。这篇博文会不断更新，目前水平有限，欢迎小伙伴们补充与指正！！！

---

降维可视化

• 通过PCA、LDA或SVD矩阵分解，将高纬数据转换为2维，便于可视化查看数据分布，了解数据特性。
  作为重点关注在算法上，而不是可视化实现的人，可视化只是辅助分析的工具，我们只需要会用即可，我觉得scikit-learn官网是个很好的学习资源，上面有很多可视化的模版。下面的代码来自scikit-learn官网中的例子：鸢尾花数据集降维可视化

  import matplotlib.pyplot as plt
  
  from sklearn import datasets
  from sklearn.decomposition import PCA
  from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
  
  iris = datasets.load_iris()
  
  X = iris.data
  y = iris.target
  target_names = iris.target_names
  
  pca = PCA(n_components=2)
  X_r = pca.fit(X).transform(X)
  
  lda = LinearDiscriminantAnalysis(n_components=2)
  X_r2 = lda.fit(X, y).transform(X)
  
  # Percentage of variance explained for each components
  print('explained variance ratio (first two components): %s'
        % str(pca.explained_variance_ratio_))
  
  plt.figure()
  colors = ['navy', 'turquoise', 'darkorange']
  lw = 2
  
  for color, i, target_name in zip(colors, [0, 1, 2], target_names):
      plt.scatter(X_r[y == i, 0], X_r[y == i, 1], color=color, alpha=.8, lw=lw,
                  label=target_name)
  plt.legend(loc='best', shadow=False, scatterpoints=1)
  plt.title('PCA of IRIS dataset')
  
  plt.figure()
  for color, i, target_name in zip(colors, [0, 1, 2], target_names):
      plt.scatter(X_r2[y == i, 0], X_r2[y == i, 1], alpha=.8, color=color,
                  label=target_name)
  plt.legend(loc='best', shadow=False, scatterpoints=1)
  plt.title('LDA of IRIS dataset')
  
  plt.show()
  

  输出
  
  
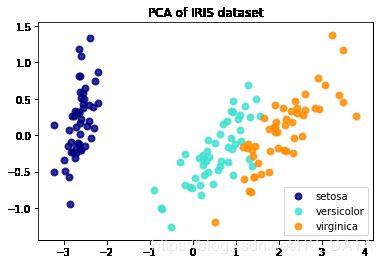
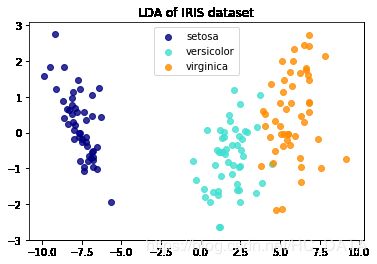
  最近做文本分类，为了形象比较词袋模型和TF-IDF模型这两种文本表示模型的效果，我借鉴了上面的降维可视化。代码如下：

from sklearn.model_selection import train_test_split
from sklearn.feature_extraction.text import CountVectorizer, TfidfVectorizer

def cv(data):
    count_vectorizer = CountVectorizer()

    emb = count_vectorizer.fit_transform(data)

    return emb, count_vectorizer

def tfidf(data):
    tfidf_vectorizer = TfidfVectorizer()

    train = tfidf_vectorizer.fit_transform(data)

    return train, tfidf_vectorizer

X = df_news["content"]
y = df_news["label"]

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)

X_train_counts, count_vectorizer = cv(X_train)
X_test_counts = count_vectorizer.transform(X_test)

X_train_tfidf, tfidf_vectorizer = tfidf(X_train)
X_test_tfidf = tfidf_vectorizer.transform(X_test)

from sklearn.decomposition import TruncatedSVD
import matplotlib.pyplot as plt

def plot_LSA(X, y):
    
    lsa = TruncatedSVD(n_components=2)
    X_lsa = lsa.fit(X).transform(X)

    target_names = iris.target_names
    
    colors = ['red','orange','yellow','green','blue','gray','black','purple']
    labels = ['国际','军事','体育','科技','财经','娱乐','时尚','汽车']
    
    plt.rcParams['font.family'] = ['Arial Unicode MS'] #正常显示中文
    for color, i in zip(colors, labels):
        plt.scatter(X_lsa[y == i, 0], X_lsa[y == i, 1], s=15, alpha=.8, c=color, label=i)
    plt.legend(loc='best', shadow=False, scatterpoints=1)
    plt.title('TruncatedSVD of news dataset')
    
    plt.show()    

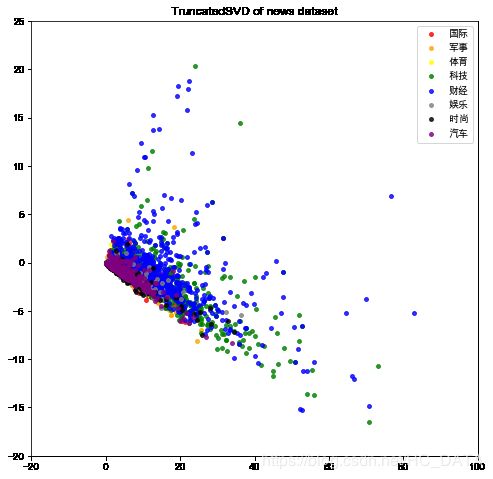
Bag of Words

fig = plt.figure(figsize=(8, 8))
axes = plt.gca()
axes.set_xlim([-20, 100])
axes.set_ylim([-20, 25])
plot_LSA(X_train_counts, y_train)

tf-idf

fig = plt.figure(figsize=(8, 8))          
plot_LSA(X_train_tfidf, y_train)

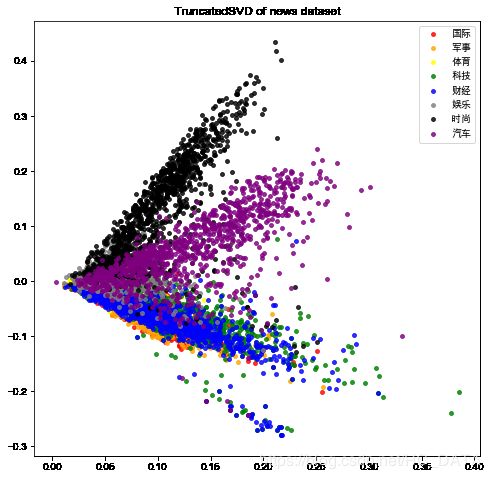
从降维可视化结果来看，词袋子模型（bag-of-words）表示下，新闻数据的可分性不是很好；文档-逆文档频率（tf-idf）文本特征表示模型让8类新闻数据的可分性变好了。这种可视化方法是不是很直观地对比了两种表示模型的效果差异呢～我们还可以将word2vec模型表示的文本特征通过这种方式可视化，看看数据集可分性是不是更好了呢！

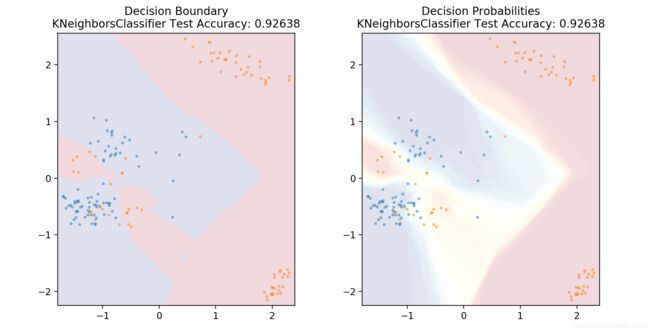
• 通过降维，我们还能绘制分类器的决策边界，下面以K近邻分类器为例：

%matplotlib notebook

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from sklearn.model_selection import train_test_split

df = pd.read_csv('mushrooms.csv')
df2 = pd.get_dummies(df)

df3 = df2.sample(frac=0.08)

X = df3.iloc[:,2:]
y = df3.iloc[:,1]


pca = PCA(n_components=2).fit_transform(X)

X_train, X_test, y_train, y_test = train_test_split(pca, y, random_state=0)


def plot_mushroom_boundary(X, y, fitted_model):

    plt.figure(figsize=(9.8,5), dpi=100)
    
    for i, plot_type in enumerate(['Decision Boundary', 'Decision Probabilities']):
        plt.subplot(1,2,i+1)

        mesh_step_size = 0.01  # step size in the mesh
        x_min, x_max = X[:, 0].min() - .1, X[:, 0].max() + .1
        y_min, y_max = X[:, 1].min() - .1, X[:, 1].max() + .1
        xx, yy = np.meshgrid(np.arange(x_min, x_max, mesh_step_size), np.arange(y_min, y_max, mesh_step_size))
        if i == 0:
            Z = fitted_model.predict(np.c_[xx.ravel(), yy.ravel()])
        else:
            try:
                Z = fitted_model.predict_proba(np.c_[xx.ravel(), yy.ravel()])[:,1]
            except:
                plt.text(0.4, 0.5, 'Probabilities Unavailable', horizontalalignment='center',
                     verticalalignment='center', transform = plt.gca().transAxes, fontsize=12)
                plt.axis('off')
                break
        Z = Z.reshape(xx.shape)
        plt.scatter(X[y.values==0,0], X[y.values==0,1], alpha=0.4, label='Edible', s=5)
        plt.scatter(X[y.values==1,0], X[y.values==1,1], alpha=0.4, label='Posionous', s=5)
        plt.imshow(Z, interpolation='nearest', cmap='RdYlBu_r', alpha=0.15, 
                   extent=(x_min, x_max, y_min, y_max), origin='lower')
        plt.title(plot_type + '\n' + 
                  str(fitted_model).split('(')[0]+ ' Test Accuracy: ' + str(np.round(fitted_model.score(X, y), 5)))
        plt.gca().set_aspect('equal');
        
    plt.tight_layout()
    plt.subplots_adjust(top=0.9, bottom=0.08, wspace=0.02)
    

from sklearn.neighbors import KNeighborsClassifier

model = KNeighborsClassifier(n_neighbors=20)
model.fit(X_train,y_train)

plot_mushroom_boundary(X_test, y_test, model)

输出

是不是很炫酷！！！

---

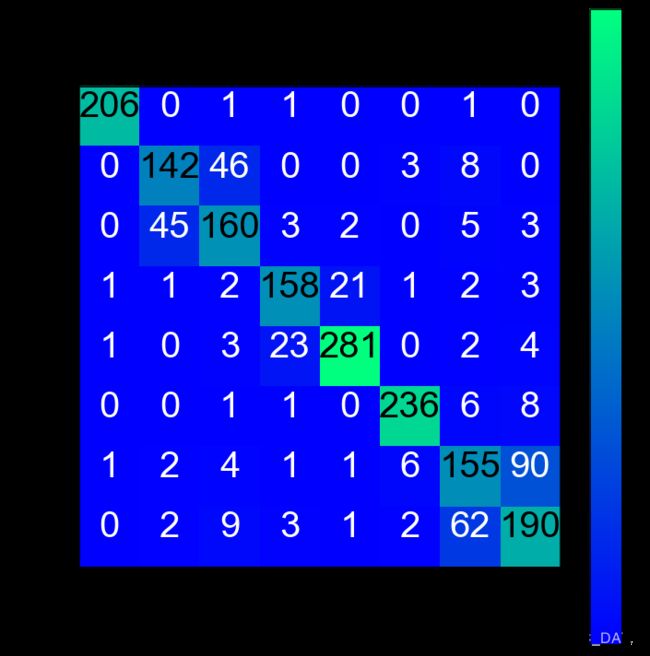
混淆矩阵可视化

• 混淆矩阵（confusion_matrix）是分类模型常用、重要的评价指标。
• 对?类分类问题，混淆矩阵为?×?的矩阵
  例:手写数字识别的混淆矩阵
  
  混淆矩阵的每一列代表了预测类别，每一列的总数表示预测为该类别的数据的数目；每一行代表了数据的真实归属类别，每一行的数据总数表示该类别的数据实例的数目。每一列中的数值表示真实数据被预测为该类的数目。
  矩阵的第?行第?列的元素值表示将真实类别标签为?类的样本预测为第?类的样本数目。对角线元素越大越好。
  下面为以文本多分类为例的混淆矩阵可视化实现：

import numpy as np
import itertools
from sklearn.metrics import confusion_matrix

def plot_confusion_matrix(cm, classes,
                          normalize=False,
                          title='Confusion matrix',
                          cmap=plt.cm.winter):
    if normalize:
        cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
    plt.imshow(cm, interpolation='nearest', cmap=cmap)
    plt.title(title, fontsize=30)
    plt.colorbar()
    tick_marks = np.arange(len(classes))
    plt.xticks(tick_marks, classes, fontsize=20)
    plt.yticks(tick_marks, classes, fontsize=20)
    
    fmt = '.2f' if normalize else 'd'
    thresh = cm.max() / 2.

    for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
        plt.text(j, i, format(cm[i, j], fmt), horizontalalignment="center", 
                 color="white" if cm[i, j] < thresh else "black", fontsize=40)
    
    plt.tight_layout()
    plt.ylabel('True label', fontsize=30)
    plt.xlabel('Predicted label', fontsize=30)

    return plt

cm = confusion_matrix(y_test, y_predicted_counts)
fig = plt.figure(figsize=(10, 10))
plot = plot_confusion_matrix(cm, classes=['体育','军事','国际','娱乐','时尚','汽车','科技','财经'], normalize=False, title='Confusion matrix')
plt.show()

输出

是不是很炫又很实用呢～

---

二分类任务指标可视化

• 在二分类任务中，我们通常还会看ROC曲线和PR曲线

• 在了解什么是ROC曲线和PR曲线之前，我们需要了解几个概念：
  

  • 精度、准确率：预测结果为真的样本中真正为真的比例
    $Precison=\frac{TP}{{\hat{N}}_{+}}$
  • 召回率：预测结果召回了多少真正的真样本
  • 真阳率：有多少真正的正样本被预测为真
    $TPR=Recall=\frac{TP}{N_{+}}$
  • 假阳率：预测结果将多少假的样本预测预测成了真
    $FPR=\frac{FP}{N_{-}}$

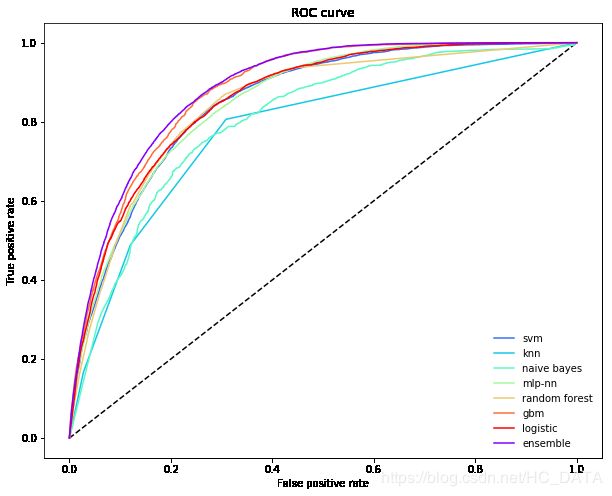
• ROC曲线
  受试者工作特征曲线 （receiver operating characteristic curve，简称ROC曲线），又称为感受性曲线（sensitivity curve）。得此名的原因在于曲线上各点反映着相同的感受性，它们都是对同一信号刺激的反应，只不过是在两种不同的判定标准下所得的结果而已。受试者工作特征曲线就是以假阳性概率（False positive rate）为横轴，真阳性（True positive rate）为纵轴所组成的坐标图，和受试者在特定刺激条件下由于采用不同的判断标准得出的不同结果画出的曲线。
  简单来说，如果不是只考虑一个阈值，而是在一些阈值上运行分类器，就能画出TPR和FPR为阈值的隐式函数，得到ROC曲线。详细说明见下图和文字：
  
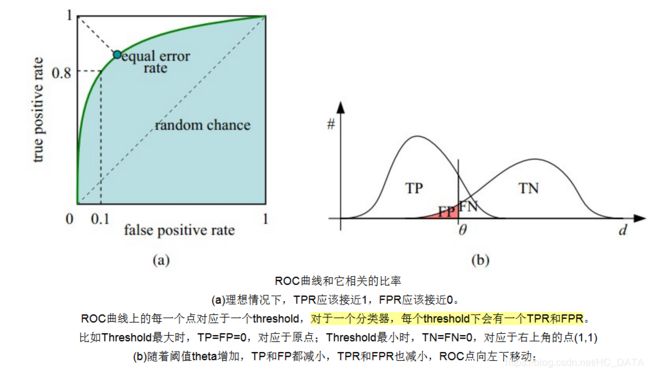
  接下来我们考虑ROC曲线图中的四个点和一条线。第一个点，(0,1)，即FPR=0, TPR=1，这意味着FN（false negative）=0，并且FP（false positive）=0。Wow，这是一个完美的分类器，它将所有的样本都正确分类。第二个点，(1,0)，即FPR=1，TPR=0，类似地分析可以发现这是一个最糟糕的分类器，因为它成功避开了所有的正确答案。第三个点，(0,0)，即FPR=TPR=0，即FP（false positive）=TP（true positive）=0，可以发现该分类器预测所有的样本都为负样本（negative）。类似的，第四个点（1,1），分类器实际上预测所有的样本都为正样本。经过以上的分析，我们可以断言，ROC曲线越接近左上角，该分类器的性能越好。

  下面考虑ROC曲线图中的虚线y=x上的点。这条对角线上的点其实表示的是一个采用随机猜测策略的分类器的结果，例如(0.5,0.5)，表示该分类器随机对于一半的样本猜测其为正样本，另外一半的样本为负样本。

  AUC（Area Under Curve）被定义为ROC曲线下的面积，显然这个面积的数值不会大于1。又由于ROC曲线一般都处于y=x这条直线的上方，所以AUC的取值范围在0.5和1之间。使用AUC值作为评价标准是因为很多时候ROC曲线并不能清晰的说明哪个分类器的效果更好，而作为一个数值，对应AUC更大的分类器效果更好。

  roc曲线绘制可以参考scikit-learn官网给出的例子：roc_plot

下面这个例子为使用不同分类器算法的roc曲线绘制，包含了集成算法：

from sklearn.metrics import roc_curve

def plot_roc_curve(ytest, P_base_learners, P_ensemble, labels, ens_label):
    """Plot the roc curve for base learners and ensemble."""
    plt.figure(figsize=(10, 8))
    plt.plot([0, 1], [0, 1], 'k--')
    
    cm = [plt.cm.rainbow(i)
      for i in np.linspace(0, 1.0, P_base_learners.shape[1] + 1)]
    
    for i in range(P_base_learners.shape[1]):
        p = P_base_learners[:, i]
        fpr, tpr, _ = roc_curve(ytest, p)
        plt.plot(fpr, tpr, label=labels[i], c=cm[i + 1])

    fpr, tpr, _ = roc_curve(ytest, P_ensemble)
    plt.plot(fpr, tpr, label=ens_label, c=cm[0])
        
    plt.xlabel('False positive rate')
    plt.ylabel('True positive rate')
    plt.title('ROC curve')
    plt.legend(frameon=False)
    plt.show()

plot_roc_curve(ytest, P.values, P.mean(axis=1), list(P.columns), "ensemble")

写到这里有点累啊！！！未完～持续更新哟！！！给个赞吧嘻嘻，感谢！