【力扣周赛】191：1464、1465、1466、1467 |回溯算法

1464：数组中两元素的最大乘积

给你一个整数数组 nums，请你选择数组的两个不同下标 i 和 j，使 (nums[i]-1)*(nums[j]-1) 取得最大值。

请你计算并返回该式的最大值。

提示：
2 <= nums.length <= 500
1 <= nums[i] <= 10^3

算法

class Solution:
    def maxProduct(self, nums: List[int]) -> int:
        nums.sort()
        return (nums[-1]-1)*(nums[-2]-1)

执行用时 :36 ms, 在所有 Python3 提交中击败了100.00%的用户
内存消耗 :13.8 MB, 在所有 Python3 提交中击败了100.00%的用户

class Solution:
    def maxProduct(self, nums: List[int]) -> int:
        a,b=0,0
        for i in nums:
            if i>b:
                b=i
                if b>a:
                    a,b=b,a
        return (a-1)*(b-1)

1465. 切割后面积最大的蛋糕

矩形蛋糕的高度为 h 且宽度为 w，给你两个整数数组 horizontalCuts 和 verticalCuts，其中 horizontalCuts[i] 是从矩形蛋糕顶部到第 i 个水平切口的距离，类似地， verticalCuts[j] 是从矩形蛋糕的左侧到第 j 个竖直切口的距离。

请你按数组 horizontalCuts 和 verticalCuts 中提供的水平和竖直位置切割后，请你找出 面积最大 的那份蛋糕，并返回其 面积 。由于答案可能是一个很大的数字，因此需要将结果对 10^9 + 7 取余后返回。

算法

脑子瓦特了才用暴力……

class Solution:
    def maxArea(self, h: int, w: int, horizontalCuts, verticalCuts) -> int:
        horizontalCuts.sort()
        verticalCuts.sort()
        res=0
        horizontalCuts=[0]+horizontalCuts+[h]
        verticalCuts=[0]+verticalCuts+[w]
        for i in range(1,len(verticalCuts)):
            for j in range(1,len(horizontalCuts)):
                res=max(res,(verticalCuts[i]-verticalCuts[i-1])*(horizontalCuts[j]-horizontalCuts[j-1]))%(10**9+7)
        return res

超时后才想起来……

class Solution:
    def maxArea(self, h: int, w: int, horizontalCuts, verticalCuts) -> int:
        horizontalCuts.sort()
        verticalCuts.sort()
        a,b=0,0
        horizontalCuts=[0]+horizontalCuts+[h]
        verticalCuts=[0]+verticalCuts+[w]
        for i in range(1,len(verticalCuts)):
            a=max(a,verticalCuts[i]-verticalCuts[i-1])

        for j in range(1,len(horizontalCuts)):
                b=max(b,horizontalCuts[j]-horizontalCuts[j-1])
        return a*b%(10**9+7)

其实就是取横着切最长的一块，和纵着切最长的一块，乘积。

1466. 重新规划路线

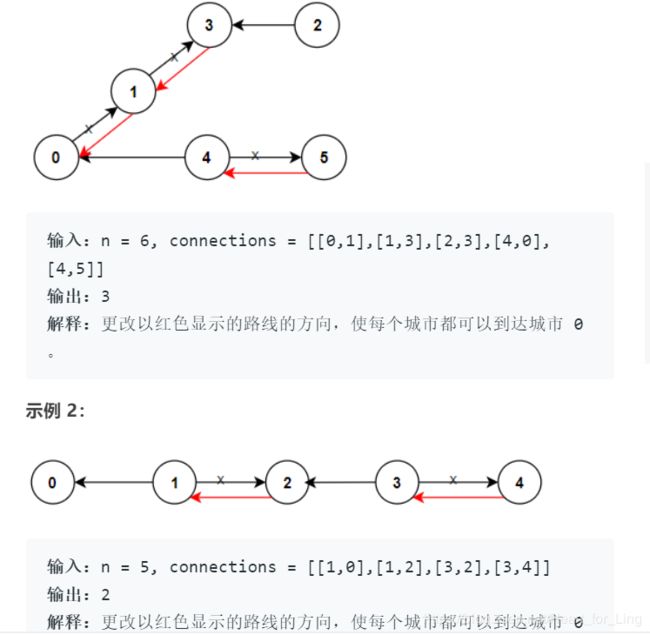
n 座城市，从 0 到 n-1 编号，其间共有 n-1 条路线。因此，要想在两座不同城市之间旅行只有唯一一条路线可供选择（路线网形成一颗树）。去年，交通运输部决定重新规划路线，以改变交通拥堵的状况。

路线用 connections 表示，其中 connections[i] = [a, b] 表示从城市 a 到 b 的一条有向路线。

今年，城市 0 将会举办一场大型比赛，很多游客都想前往城市 0 。

请你帮助重新规划路线方向，使每个城市都可以访问城市 0 。返回需要变更方向的最小路线数。

题目数据 保证 每个城市在重新规划路线方向后都能到达城市 0 。

提示：
2 <= n <= 5 * 10^4
connections.length == n-1
connections[i].length == 2
0 <= connections[i][0], connections[i][1] <= n-1
connections[i][0] != connections[i][1]

算法

观察实例，很轻易的想到了广度优先搜索，

1. 从0出发（把0放入集合），将所有与0相连的线路检查一遍是否需要逆转，然后把相邻城市放入集合，把链接从connections中剔除
2. 更新集合，重复第一步，直到connections为空。

class Solution:
    def minReorder(self, n: int, connections) -> int:
        res=0
        ls={0}
        while connections:
            i=0
            tp=set()
            while i<len(connections):
                if connections[i][0] in ls:
                    res+=1
                    tp.add(connections[i][1])
                    connections.pop(i)
                elif connections[i][1] in ls:
                    tp.add(connections[i][0])
                    connections.pop(i)
                else:
                    i+=1
            ls=tp.copy()
        return res

执行用时 :704 ms, 在所有 Python3 提交中击败了100.00%的用户
内存消耗 :22.3 MB, 在所有 Python3 提交中击败了100.00%的用户

1467. 两个盒子中球的颜色数相同的概率

桌面上有 2n 个颜色不完全相同的球，球上的颜色共有 k 种。给你一个大小为 k 的整数数组 balls ，其中 balls[i] 是颜色为 i 的球的数量。

所有的球都已经 随机打乱顺序 ，前 n 个球放入第一个盒子，后 n 个球放入另一个盒子（请认真阅读示例 2 的解释部分）。

注意：这两个盒子是不同的。例如，两个球颜色分别为 a 和 b，盒子分别为 [] 和 ()，那么 [a] (b) 和 [b] (a) 这两种分配方式是不同的（请认真阅读示例 1 的解释部分）。

请计算「两个盒子中球的颜色数相同」的情况的概率。

示例 1：
输入：balls = [1,1]
输出：1.00000
解释：球平均分配的方式只有两种：
- 颜色为 1 的球放入第一个盒子，颜色为 2 的球放入第二个盒子
- 颜色为 2 的球放入第一个盒子，颜色为 1 的球放入第二个盒子
这两种分配，两个盒子中球的颜色数都相同。所以概率为 2/2 = 1 。

示例 2：
输入：balls = [2,1,1]
输出：0.66667
解释：球的列表为 [1, 1, 2, 3]
随机打乱，得到 12 种等概率的不同打乱方案，每种方案概率为 1/12 ：
[1,1 / 2,3], [1,1 / 3,2], [1,2 / 1,3], [1,2 / 3,1], [1,3 / 1,2], [1,3 / 2,1], [2,1 / 1,3], [2,1 / 3,1], [2,3 / 1,1], [3,1 / 1,2], [3,1 / 2,1], [3,2 / 1,1]
然后，我们将前两个球放入第一个盒子，后两个球放入第二个盒子。
这 12 种可能的随机打乱方式中的 8 种满足「两个盒子中球的颜色数相同」。
概率 = 8/12 = 0.66667

示例 3：
输入：balls = [1,2,1,2]
输出：0.60000
解释：球的列表为 [1, 2, 2, 3, 4, 4]。要想显示所有 180 种随机打乱方案是很难的，但只检查「两个盒子中球的颜色数相同」的 108 种情况是比较容易的。
概率 = 108 / 180 = 0.6 。

示例 4：
输入：balls = [3,2,1]
输出：0.30000
解释：球的列表为 [1, 1, 1, 2, 2, 3]。要想显示所有 60 种随机打乱方案是很难的，但只检查「两个盒子中球的颜色数相同」的 18 种情况是比较容易的。
概率 = 18 / 60 = 0.3 。

示例 5：
输入：balls = [6,6,6,6,6,6]
输出：0.90327
 

提示：
1 <= balls.length <= 8
1 <= balls[i] <= 6
sum(balls) 是偶数
答案与真实值误差在 10^-5 以内，则被视为正确答案

算法

class Solution:
    def getProbability(self, balls: List[int]) -> float:
        # 球数， 颜色数
        n, nc = sum(balls), len(balls)
        
        # 总方案数
        self.k = 0
        
        # 取到第i种球，1盒球数, 1盒颜色数, 2盒球数，2盒颜色数，方案数    
        def dfs(i, m1, mc1, m2, mc2, k):
            # 剪枝
            if m1 > n//2 or m2 > n//2:
                return 
            if i == nc:
                if m1 == m2 and mc1 == mc2 :
                    self.k += k
                return     
            for dm in range(balls[i]+1):     
                dfs(i + 1, m1 + dm, mc1 + (dm != 0), m2 + balls[i] - dm, mc2 + (dm != balls[i]), k*comb(balls[i], dm))
                
        dfs(0, 0, 0, 0, 0, 1)        
        return self.k/comb(n, n//2) 

直接贴的大佬的算法，啊，实在不想去想了。
comb是math 下的函数，python3.8以后才有。