基带传输系统的奈奎斯特准则与奈奎斯特速率
奈奎斯特准则与带限信道可行的码元速率探究(篇二):无码间串扰与奈奎斯特准则
写在前:
本篇是《奈奎斯特准则与带限信道可行的码元速率探究》的篇二,基础知识部分。主要介绍了基带传输系统中的码间串扰的解决、奈奎斯特准则与奈奎斯特速率。本系列文章的篇一:什么是码间串扰介绍了码间串扰的基本概念和原理。
为了最好地传输数字信号,应该保证接收时没有码间串扰,根据:什么是码间串扰可知需要传输系统总的冲击响应 h ( t ) h(t) h(t)满足 h ( n T s ) = { h ( 0 ) = 常 数 , n = 0 = h ( 0 ) δ [ n ] 式 ( 1 ) 0 , n ≠ 0 h(nT_s)= \left\{ \begin{array}{ll}h(0)=常数,\ \ \ n=0\\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =h(0)\delta[n] \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 式(1)\\0,\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ n\neq0\end{array} \right. h(nTs)=⎩⎨⎧h(0)=常数, n=0 =h(0)δ[n] 式(1)0, n̸=0
即, h ( t ) h(t) h(t)的抽样序列是数字冲激序列 δ [ n ] \delta[n] δ[n](这里不妨考虑归一化后的 h ( t ) h(t) h(t))。
式(1)这一条件是数字基带传输系统无码间串扰的充要条件,它也可以用传输系统总的频率响应 H ( f ) H(f) H(f)(从频域上)来表述,被称为奈奎斯特(Nyquist)准则。
奈奎斯特准则:
定理(Nyquist准则) 数字基带传输系统无码间串扰的充要条件是式(1),其频域形式为 ∑ k = − ∞ ∞ H ( t − k / T s ) = 常 数 式 ( 2 ) \sum_{k=-\infty}^\infty H(t-k/T_s)=常数\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 式(2) k=−∞∑∞H(t−k/Ts)=常数 式(2)
其中 R s = 1 / T s R_s=1/T_s Rs=1/Ts,即码元速率,于是该定理又有形式 ∑ k = − ∞ ∞ H ( t − k ⋅ R s ) = 常 数 \sum_{k=-\infty}^\infty H(t-k\cdot R_s)=常数 ∑k=−∞∞H(t−k⋅Rs)=常数。
证明 根据前面ISI的分析,这一结论的时域部分是明显的,而频域部分可以如下说明。
F [ ∑ n = − ∞ ∞ δ ( t − n T s ) ] = 1 T s ∑ k = − ∞ ∞ δ ( f − k / T s ) , F [ δ [ n ] ] = 1 \mathcal{F}\bigg[\sum_{n=-\infty}^\infty \delta(t-nT_s)\bigg]=\frac{1}{T_s}\sum_{k=-\infty}^\infty \delta(f-k/T_s),\mathcal{F}\big[\delta[n] \big]=1 F[n=−∞∑∞δ(t−nTs)]=Ts1k=−∞∑∞δ(f−k/Ts),F[δ[n]]=1
h ( n T s ) = h ( t ) ∑ n = − ∞ ∞ δ ( t − n T s ) ⟷ H ( f ) ∗ [ 1 T s ∑ k = − ∞ ∞ δ ( f − k / T s ) ] = 1 T s ∑ k = − ∞ ∞ H ( f − k / T s ) h(nT_s)=h(t)\sum_{n=-\infty}^\infty\delta(t-nT_s)\longleftrightarrow H(f)\ast\bigg[\frac{1}{T_s}\sum_{k=-\infty}^\infty \delta(f-k/T_s)\bigg]=\frac{1}{T_s}\sum_{k=-\infty}^\infty H(f-k/T_s) h(nTs)=h(t)n=−∞∑∞δ(t−nTs)⟷H(f)∗[Ts1k=−∞∑∞δ(f−k/Ts)]=Ts1k=−∞∑∞H(f−k/Ts)
根据式(1)可得: 1 T s ∑ k = − ∞ ∞ H ( f − k / T s ) = h ( 0 ) ( 常 数 ) \frac{1}{T_s}\sum_{k=-\infty}^\infty H(f-k/T_s)=h(0)(常数) Ts1k=−∞∑∞H(f−k/Ts)=h(0)(常数)
于是定理得证。
Nyquist准则的含义是:判断任何信道是否含有ISI的有效方法是计算并观察 ∑ k = − ∞ ∞ H ( f − k ⋅ R s ) \sum_{k=-\infty}^\infty H(f-k\cdot R_s) ∑k=−∞∞H(f−k⋅Rs)是否为常数。由于它是 H ( f ) H(f) H(f)按 R s R_s Rs周期重复的结果,一定是周期为 R s R_s Rs的函数,因此,只需观察它在 ( − R s / 2 , R s / 2 ) (-R_s/2,R_s/2) (−Rs/2,Rs/2)上是否为常数就可以做出判断。
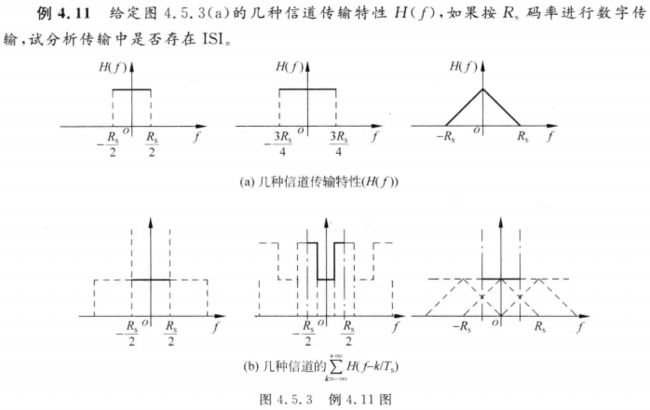

现在我们讨论一下基带信道的无码间串扰。由于基带信道是带限(低通)的,于是传输系统的频响函数也是带限的。假定 H ( f ) H(f) H(f)的带宽为 W W W,传输系统欲以 R s = 1 / T s R_s=1/T_s Rs=1/Ts的码率通过它传输数字序列,依据奈奎斯特准则,会出现下面三种情况:
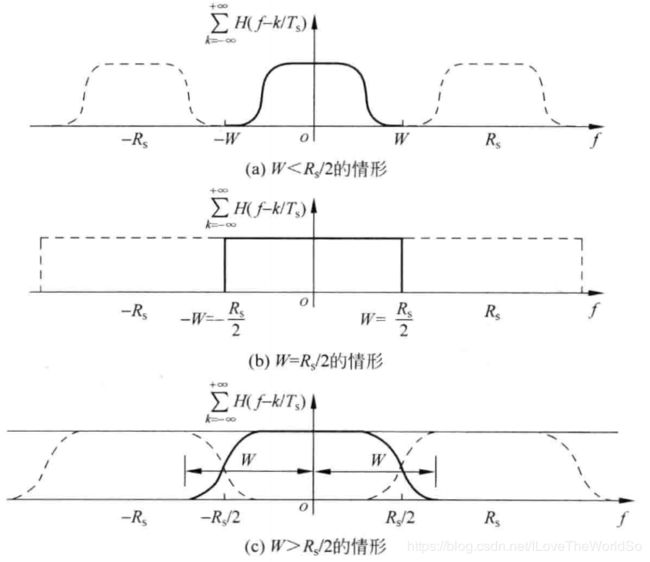
图 1 带 限 信 道 ∑ k = − ∞ ∞ H ( t − k ⋅ R s ) 图1\ 带限信道\sum_{k=-\infty}^\infty H(t-k\cdot R_s) 图1 带限信道k=−∞∑∞H(t−k⋅Rs)
(1) R s > 2 W R_s>2W Rs>2W:如图1.(a)所示,将 H ( f ) H(f) H(f)按周期 R s R_s Rs重复后根本无法形成常数频谱,因此,该系统无法满足奈奎斯特准则,接收中一定存在码间串扰;
(2) R s = 2 W R_s=2W Rs=2W:如图1.(b)所示,当且仅当 H ( f ) H(f) H(f)正好为 R s / 2 R_s/2 Rs/2的理想LPF(理想低通滤波器)时,它按 R s R_s Rs周期重复后恰好可构成常数频谱。因此,无码间串扰接收的充要条件为 H ( f ) H(f) H(f)是如下的理想LPF H ( f ) = { 常 数 , ∣ f ∣ ⩽ R s 式 ( 3 ) 0 , ∣ f ∣ > R s H(f)= \left\{ \begin{array}{ll}常数,\ \ \ |f|\leqslant R_s\\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 式(3)\\0,\ \ \ \ \ \ \ \ \ |f|>R_s\end{array} \right. H(f)=⎩⎨⎧常数, ∣f∣⩽Rs 式(3)0, ∣f∣>Rs
(3) R s < 2 W R_s<2W Rs<2W:如图1.(c)所示,这时,有可能找到某些合适的 H ( f ) H(f) H(f),周期重复时满足奈奎斯特准则,从而保证接收时无码间串扰。
由上面的讨论可以立即得到一个简明的关系式,在无码间串扰的条件下必有: R s ⩽ 2 W R_s\leqslant2W Rs⩽2W。
在关于理想LPF的码率的介绍中,我的老师比较严谨地补充到:理想LPF的码率上限就是 2 W 2W 2W,当码率低于 2 W 2W 2W时,有可能满足无码间串扰,就是说有的速率可以有的速率不可以,具体条件他尚未探究过,有兴趣可以自行探究。
关于上面这一段话我产生了疑惑和思考:理想低通滤波器的码率存在着 R s max = 2 W R_{s\ \max}=2W Rs max=2W的限制让我在常识上很容易接受,但是却又有 R s < 2 W R_s<2W Rs<2W不一定满足无码间串扰的意思。按照我自己本来的直觉既然码率有上限,那么当码率低于这个上限就应该满足无码间串扰了;就像存在一个固定容量的单车道(类比理想低通信道,即理想LPF),每前后两辆车(类比码元)存在着安全距离(最小传输时间间隔,类比 T s T_s Ts),车与车之间可以按照任意大过安全距离的距离行驶,只是信道的传输效率不同而已。不过,抽样判决得到的序列又确实与抽样时间间隔有关,那码元速率(也即码元间隔)在低于极限时也确实应该存在着限制。
那么,对于理想LPF的码元速率究竟有着具体怎样的形式和限制呢?我们就用已经证明的奈奎斯特定理进行进一步的探究吧!参见《奈奎斯特准则与带限信道可行的码元速率探究》的篇三,理想低通滤波器的可行码元速率探究。
注:本篇中的部分内容和图例参考了李晓峰主编的《通信原理》