为什么BTree/B+Tree作为数据库或者文件索引效率很高
部分参考:MySQL索引原理及BTree(B-/+Tree)结构详解
BTree有很多种分类,也可以说是基于BTree实现了其他类似BTree的结构,MySQL的默认索引方式为B+Tree,这里就从B+Tree的查找效率和计算机组成原理来讨论为什么BTree作为数据库索引效率很高,红黑树等数据结构也可以用来实现索引,为什么不选择这个结构?
一般来说,索引本身也很大,不可能全部存储在内存中,因此索引往往以索引文件的形式存储的磁盘上。这样的话,索引查找过程中就要产生磁盘I/O消耗,相对于内存存取,I/O存取的消耗要高几个数量级,所以评价一个数据结构作为索引的优劣最重要的指标就是在查找过程中磁盘I/O操作次数的渐进复杂度。换句话说,索引的结构组织要尽量减少查找过程中磁盘I/O的存取次数。下面先介绍内存和磁盘存取原理,然后再结合这些原理分析BTree作为索引的效率。
从计算机组成原理的角度
主存存取原理
目前计算机使用的主存基本都是随机读写存储器(RAM),现代RAM的结构和存取原理比较复杂,这里本文抛却具体差别,抽象出一个十分简单的存取模型来说明RAM的工作原理。
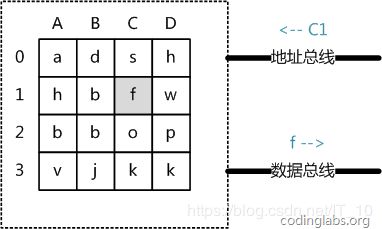
从抽象角度看,主存是一系列的存储单元组成的矩阵,每个存储单元存储固定大小的数据。每个存储单元有唯一的地址,现代主存的编址规则比较复杂,这里将其简化成一个二维地址:通过一个行地址和一个列地址可以唯一定位到一个存储单元。上图展示了一个4 x 4的主存模型。
主存的存取过程如下:
当系统需要读取主存时,则将地址信号放到地址总线上传给主存,主存读到地址信号后,解析信号并定位到指定存储单元,然后将此存储单元数据放到数据总线上,供其它部件读取。
写主存的过程类似,系统将要写入单元地址和数据分别放在地址总线和数据总线上,主存读取两个总线的内容,做相应的写操作。
这里可以看出,主存存取的时间仅与存取次数呈线性关系,因为不存在机械操作,两次存取的数据的“距离”不会对时间有任何影响,例如,先取A0再取A1和先取A0再取D3的时间消耗是一样的。
磁盘存取原理
上文说过,索引一般以文件形式存储在磁盘上,索引检索需要磁盘I/O操作。与主存不同,磁盘I/O存在机械运动耗费,因此磁盘I/O的时间消耗是巨大的。

一个磁盘由大小相同且同轴的圆形盘片组成,磁盘可以转动(各个磁盘必须同步转动)。在磁盘的一侧有磁头支架,磁头支架固定了一组磁头,每个磁头负责存取一个磁盘的内容。磁头不能转动,但是可以沿磁盘半径方向运动(实际是斜切向运动),每个磁头同一时刻也必须是同轴的,即从正上方向下看,所有磁头任何时候都是重叠的(不过目前已经有多磁头独立技术,可不受此限制)。
磁盘结构的示意图:
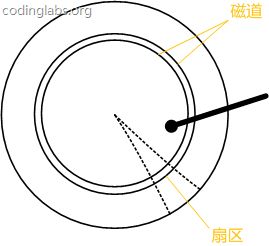
盘片被划分成一系列同心环,圆心是盘片中心,每个同心环叫做一个磁道,所有半径相同的磁道组成一个柱面。磁道被沿半径线划分成一个个小的段,每个段叫做一个扇区,每个扇区是磁盘的最小存储单元。为了简单起见,我们下面假设磁盘只有一个盘片和一个磁头。
当需要从磁盘读取数据时,系统会将数据逻辑地址传给磁盘,磁盘的控制电路按照寻址逻辑将逻辑地址翻译成物理地址,即确定要读的数据在哪个磁道,哪个扇区。为了读取这个扇区的数据,需要将磁头放到这个扇区上方,为了实现这一点,磁头需要移动对准相应磁道,这个过程叫做寻道,所耗费时间叫做寻道时间,然后磁盘旋转将目标扇区旋转到磁头下,这个过程耗费的时间叫做旋转时间。
局部性原理与磁盘预读
由于存储介质的特性,磁盘本身存取就比主存慢很多,再加上机械运动耗费,磁盘的存取速度往往是主存的几百分分之一,因此为了提高效率,要尽量减少磁盘I/O。为了达到这个目的,磁盘往往不是严格按需读取,而是每次都会预读,即使只需要一个字节,磁盘也会从这个位置开始,顺序向后读取一定长度的数据放入内存。这样做的理论依据是计算机科学中著名的局部性原理:
当一个数据被用到时,其附近的数据也通常会马上被使用。
也就是说,程序运行期间所需要的数据通常比较集中。
由于磁盘顺序读取的效率很高(不需要寻道时间,只需很少的旋转时间),因此对于具有局部性的程序来说,预读可以提高I/O效率。
预读的长度一般为页(page)的整倍数。页是计算机管理存储器的逻辑块,硬件及操作系统往往将主存和磁盘存储区分割为连续的大小相等的块,n个块的组合称为页,主存和磁盘以页为单位交换数据。当程序要读取的数据不在主存中时,会触发一个缺页异常,此时系统会向磁盘发出读盘信号,磁盘会找到数据的起始位置并向后连续读取一页或几页载入内存中,然后异常返回,程序继续运行。
最小存储单元
扇区:磁盘的最小存储单位。扇区是块设备传输数据的基本单元,也就是说它是块设备中最小的寻址单位,扇区通常的大小为512B。
块:文件系统读写数据的最小单位。块是内核对文件系统的一种抽象,也就是说内核执行的所有磁盘操作都是以块为基本单位的。
页:内存的最小存储单位。
可以简单的将扇区和块理解为:扇区是硬件设备传输数据的最小单位,而块是操作系统传输数据的最小单位。一个块通常对应一个或多个相邻的扇区。一页的大小为磁盘块大小的2的n(n为正整数)次方倍。
总结:在计算机中,磁盘存储数据最小单元是扇区,一个扇区大小为512字节,而文件系统的最小存储单元是块,一个块的大小是4k(即如果一个文件及时只有1k,在磁盘上占的空间也是4k)。
说了这么多,我就是想表明InnoDB引擎的最小存储单元是页,一页默认值为16KB(MySQL5.5以前,一页固定为16k,MySQL5.5以后,页大小为4KB, 8KB, 或者16KB,MySQL5.7.6还支持32KB和64KB,但是默认情况下都是16KB,参见官网 https://dev.mysql.com/doc/refman/5.7/en/glossary.html#glos_page_size )。这个概念对后面计算InnoDB引擎中一棵B+Tree可以存放多少行数据很重要。
BTree/B+Tree索引的性能分析
BTree/B+Tree作为索引的结构请看:MySQL索引详解 这篇文章的“索引的方式”小结详细讲解了该结构。
生成的索引结构是一个映射表存储在磁盘中,通常比较大,而索引文件的读取决于磁盘I/O的速度,计算机科学中有局部性原理与磁盘预读,数据库设计者正是巧妙地利用了磁盘预读原理,将一个节点的大小设为等于一个页,这样每个节点只需要一次I/O就可以完全载入。为了达到这个目的,在实际实现B-Tree还需要使用如下技巧:
每次新建节点时,直接申请一个页的空间,这样就保证一个节点物理上也存储在一个页里,加之计算机存储分配都是按页对齐的,就实现了一个node只需一次I/O。
除了利用磁盘预读原理外,mysql 把每个节点的空间大小设置为一个页还有一个原因是每个节点中的数据可能会分散到不同数据块中,因此把每个节点的空间大小设置为一个页,这样就能保证每个节点只需要一次IO。
这是一种以空间换时间的方法。
BTree中一次检索最多需要h-1(h为树的高度)次I/O(根节点常驻内存),渐进复杂度为O(h)=O(logdN)O(h)=O(logdN)。一般实际应用中,出度d是非常大的数字,通常超过100,因此h非常小(通常不超过3)。
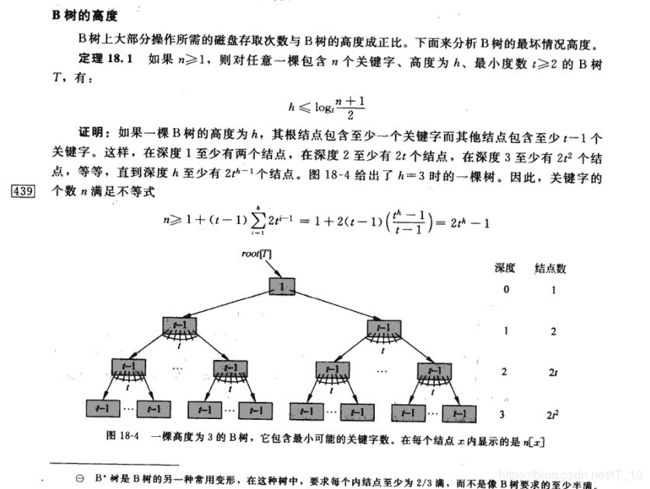
注:书上说的是一棵高度为3的B树,因为他是从0开始计数的
综上所述,用BTree作为索引结构效率是非常高的。而且d越大索引的性能越好,而出度的上限取决于节点内key和data的大小(因为一个节点占一页,通常是4k,所以要保证keysize+datasize+pointsize不超过4K,因此去掉datasize,d会更大):
dmax=floor(pagesize/(keysize+datasize+pointsize))floor表示向下取整。
由于B+Tree内节点去掉了data域,因此可以拥有更大的出度,拥有更好的性能。
而红黑树这种结构,h明显要深的多。由于逻辑上很近的节点(父子)物理上可能很远,无法利用局部性,所以红黑树的I/O渐进复杂度也为O(h),效率明显比B-Tree差很多。
从BTree/B+Tree查找的角度
上面提到BTree/B+Tree中一次检索最多需要h-1次I/O,这里肯定是需要从根节点开始搜索BTree/B+Tree,根节点就在内存中,下面先贴出一个高度为3的B+Tree- 先从内存中对更节点进行搜索找到下一个节点的指针,由于一个节点上的数据是有序的,因此可以用二分查找,定位到第二层坐左边的节点。
- 将该页的数据从磁盘上读取到内存,再按照二分查找定位到最后一层中间的节点。
- 从磁盘上读取该节点到内存中,找到20,取出数据
这一过程进行了2次I/O操作,3次内存查找操作,并且二分查找的时间复杂度为O(log2n)。
InnoDB引擎中一棵B+Tree可以存放多少行数据?
InnoDB引擎中的B+Tree结构在MySQL索引详解一文中已经讲解过,这里我再次把图贴出来为了方便看。
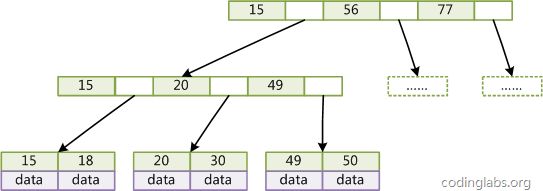
B+Tree中,一个节点设计为一个页的大小16K,假设一行记录的数据大小为nK,B+Tree的高度为t(t的值一般取1~3),主键的长度为p字节,指针大小在InnoDB源码中设置为6字节
先计算非叶子节点能存放多少个指针和键值的组合?
指针和键值的组合占p+6字节,因此答案是[16*1024]/(p+6)个,这个结果记为A
再把数的高度带入计算,得到InnoDB引擎中一棵B+Tree可以存放多少行数据?
答案是: (A ^t) *(16/n)
举例
一行记录的大小是1k,则一页能存16条记录,B+Tree高度是3,主键id设为bigint(8字节),一个节点最大能存16*1024=16384字节的数据,指针在InnoDB中是6字节,则主键+指针的大小是14字节,一个非叶子节点能存16384/14=1170个主键+指针的组合,因此对于高度为3的B+Tree,能存1170 * 1170 * 16=21902400条记录。
InnoDB引擎中为什么推荐使用自增整型主键
因为整型比较大小比字符串效率块,这样在B+Tree节点内查找的时候就会快点,并且整型存储空间一般也更小,bigint就8字节。而且InnoDB引擎使用的是带指针的B+Tree,即叶子节点用指针连起来,如果使用自增主键,新增记录时,直接在最后一个节点插入即可,增加了插入效率。否则在B+Tree中插入节点会导致节点分裂等影响效率的问题。
InnoDB引擎中为什么必须要指定主键(未指定会启用虚拟主键)
因为InnoDB擎中的数据表本身就是B+Tree结构存储数据和主键索引的(数据和索引存储在一起)。所以指定主键构建B+Tree结构的主键索引+数据文件提高查找效率。
