cs224w 图神经网络 学习笔记（一）Introduction

课程链接：CS224W: Machine Learning with Graphs
课程视频：【课程】斯坦福 CS224W: 图机器学习 (2019 秋 | 英字)

0. 写在前面

第一节课是Introduction，主要介绍了图的优势以及图论的一些基本概念。

1. Why Networks？

首先，我们先来看一下什么是Networks（网络）。

Networks are a general language for describing complex systems of interating entities.
网络是一种描述复杂系统中关联实体的通用语言。

那么，对于这样的一种“通用语言”，我们不禁会产生两个问题：

1. How are these system organized?
2. What are their design properties?

我们只有弄清楚这些系统背后的网络模型，才有可能真正地对这些系统进行建模、解析、预测、深度利用。

在我们的生活中，其实很多数据都是以网络/图的形式存在的。网络可以大致分为两类，不过这两类网络有时候界限没有那么明显：

1. Networks (Natural Graphs)
   第一类可以看做是自然网络，比如社会、社交网络、蛋白质图谱、基因图谱、思维导图等。
2. Information Graphs
   第二类就是各种信息汇聚成为的网络，如知识图谱，相似网络（similarity netoworks）等等。

那么，为什么要研究网络呢？
主要有下面几点原因：

目前对于网络的研究主要集中在以下几个方面/场景：

1. 对节点的类型/属性进行预测。例如：节点分类。
2. 预测两个节点是否相连。例如：链路预测（link prediction）。
3. 识别紧密相连的节点群。例如：社区挖掘（Community detection），节点聚类。
4. 计算两个节点或者网络的相似性。

2. 基础：网络/图论基本知识

2.1 Starter Topic: Structure of Graphs 图的结构

网络（Networks）的结构使怎么样的呢？我们先来看一下它的定义：

A network is a collection of objects where some pairs of objects are connected by links
网络是互连成对的节点的集合。

网络的结构有三类重要的元素：

• Objects（对象）：Nodes（节点）、顶点（Vertices），用$N$来表示。
• Interactions（相互作用）: links（链接）, edges（边），用$E$来表示。
• System（系统） ¹ : network（网络）, graph（图），用$G(N,E)$来表示。

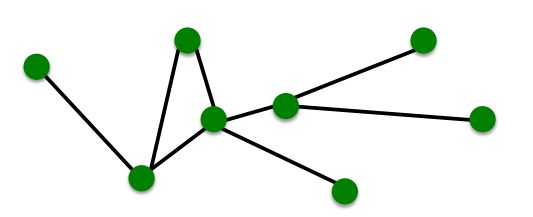
那么，构建一个网络/图，就是定义它的这些基本结构——哪些信息/元素作为节点，这些节点之间怎么进行连接（即边怎么定义）。对于不同的场景，选择合适的图来进行描述和建模，会变得事半功倍。

同时，很多时候，图的结构使不唯一的，你怎么定义图的结构，取决于你要研究/解决什么问题。

2.2 Choice of Network Representation 图的不同形式

有向图和无向图

	无向图	有向图
图例
特点	undirected (symmetrical, reciprocal)	directed (arcs)
例子	合作关系，微信中的好友关系	微博上的follow关系
度（Node degrees）	在无向图中，点的度为与其相连的边的数量。如图中D点的度$k_D=5$。在图中，所有节点的度与边存在以下关系：$\overline{k}=⟨k⟩=\frac{1}{N}{\sum }_{i=1}^N{k}_i=\frac{2E}{N}$。	在有向图中，有入度（in-degree）和出度（out-degree）之分。如图中B点的入度$k{}_B^{in}=1$，出度$k{}_B^{out}=2$，B点的度为其入度与出度之和，即$k_B=k{}_B^{in}+k{}_B^{out}=1+2=3$。而对于整张图来说，$\overline{k}=\frac{E}{N}$且$k_{in}=k_{out}$ 。

完全图(Complete Graph)
在图论的数学领域，完全图是一个简单的无向图，其中每对不同的顶点之间都恰连有一条边相连。

二分图（Bipartite graph，二部图，对偶图）

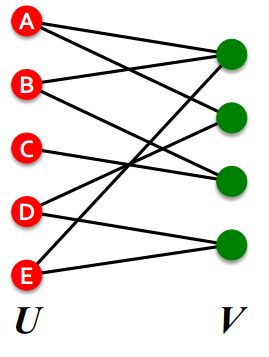
二分图	二分图的折叠(folded) /投影(projection)

在二分图中，图的节点恰好可以分为两个互不相交的集合$U$和$V$，图中每条边都是这两个集合中的节点的链接。二分图是一种十分常见的图数据对象，描述了两类对象之间的交互关系，如：用户与商品，作者与文章。

二分图的折叠(folded) /投影(projection) 是指若该集合中的某些节点如果有链接到另一个集合的同一个节点，则认为他们之间存在一定的关系。

加权图（Weighted graph）与非加权图（Unweighted graph）

连通图与非连通图
如果图中存在孤立的顶点，没有任何边与之相连，这样的图被称为非连通图。反之，如果不存在孤立顶点的图称为连通图。

其他类型的图

2.3 图的存储

邻接矩阵（Adjacency matrix）
邻接矩阵中$A_{ij}=1$表示有边连接（指向）节点$i$到节点$j$；否则，$A_{ij}=0$。

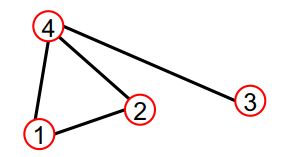
无向图	有向图

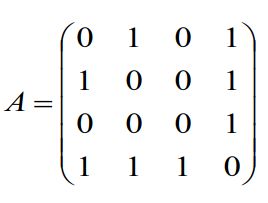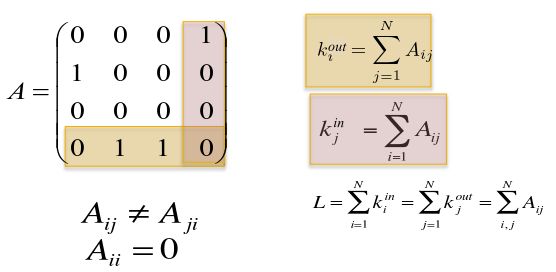现实中，在大多数情况下，邻接矩阵表现为稀疏矩阵。并且现实中的网络是稀疏的。

关联矩阵
关联矩阵中$B_{ij}$的定义如下：
$$B_{ij}=\{\begin{array}{ll}1,& \text{if vi 与 ej 相连}\\ 0,& \text{otherwise}\end{array}$$

边列表（Edge list）
将图表示为边的的集合。

如上图就可以表示为$\{(1,4),(2,1),(4,2),(4,3)\}$。

邻接列表（Adjacency list）
当图变得很大、邻接矩阵很稀疏时，使用邻接列表对图进行存储是一个不错的选择。邻接列表实质上是一个dict。例如：

上图的邻接列表为{1:[], 2:[3,4], 3:[2,4], 4:[5], 5:[1,2]}。

---

1. 需要注意的是，网络（Networks）通常是指真实存在的系统，如社交网络（Social Networks）。通常Network、Node、Link会放在一起使用。而图（Graph）更偏向于表示网络的数学表述，通常Graph、Vertex、Edge会放在一起使用。很多地方对于这两个概念没有特别明显的区别。 ↩︎