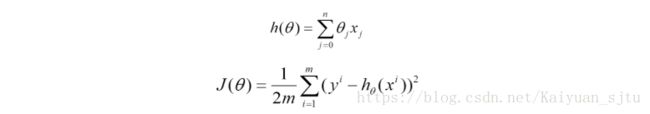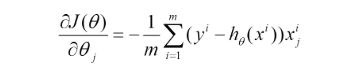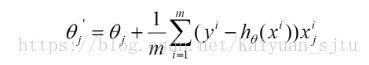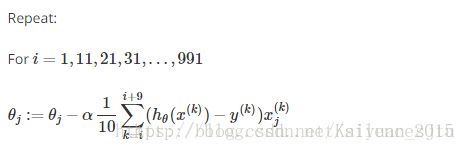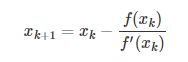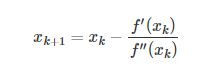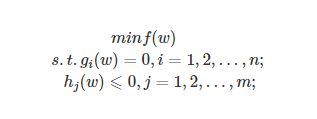机器学习中常用的优化方法

写在前面

在看斯坦福的次cs231n课程，里面提到一些机器学习的基础知识，比如损失函数，优化算法，正则化形式等等。然后有一些知识也都记不起来了，索性就在博客上再回顾一遍顺便记录下来日后方便查阅。今天就先整理机器学习算法中常用的几种优化损失函数的优化方法，主要有：

梯度下降法、

牛顿法和拟牛顿法、

共轭梯度法、

启发式优化方法以及解决约束优化问题的拉格朗日乘数法。

1. 梯度下降法（Gradient Descent）

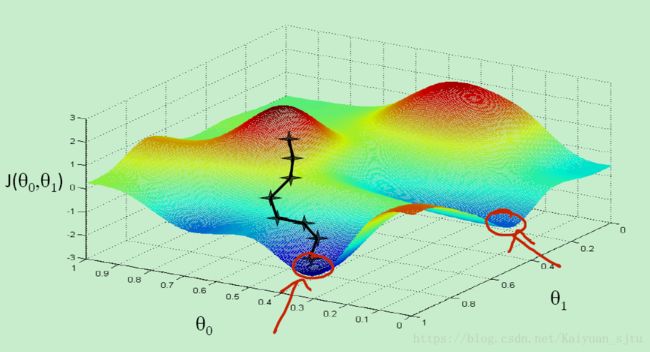
梯度下降法是最早最简单，也是最为常用的最优化方法。梯度下降法实现简单，当目标函数是凸函数时，梯度下降法的解是全局解。一般情况下，其解不保证是全局最优解，梯度下降法的速度也未必是最快的。梯度下降法的优化思想是用当前位置负梯度方向作为搜索方向，因为该方向为当前位置的最快下降方向，所以也被称为是”最速下降法“。最速下降法越接近目标值，步长越小，前进越慢。在解释梯度下降法时使用最多的一幅图如下：

在机器学习中，基于基本的梯度下降法发展了几种梯度下降方法，分别为随机梯度下降法、批量梯度下降法以及小批量梯度下降法。

比如对一个线性回归（Linear Logistics）模型，假设下面的h(x)是要拟合的函数，J(theta)为损失函数，theta是参数，要迭代求解的值，theta求解出来了那最终要拟合的函数h(theta)就出来了。其中m是训练集的样本个数，n是特征的个数。

1.1 批量梯度下降（Batch gradient descent）

BGD优化算法的过程如下：

• 将J(theta)对theta求偏导，得到每个theta对应的的梯度：

• 由于是要最小化风险函数，所以按每个参数theta的梯度负方向，来更新每个theta：

从上面公式可以注意到，对于凸函数它得到的是一个全局最优解，对于非凸的损失函数它得到的可能是局部最优解。但是每迭代一步，都要用到训练集所有的数据，如果m很大，那么可想而知这种方法的迭代速度会相当的慢。

BGD的代码可以这样表示：

for i in range(n_epochs):
    params_grad = evaluate_gradient(loss_function, data, params)
    params = params - learning_rate * params_grad

所以，这就引入了另外一种方法——随机梯度下降。

1.2 随机梯度下降（Stochastic Gradient Descent）

SGD优化算法的过程如下：

• 上面的风险函数可以写成如下这种形式，损失函数对应的是训练集中每个样本的粒度，而上面批量梯度下降对应的是所有的训练样本：

 

• 每个样本的损失函数，对theta求偏导得到对应梯度，来更新theta：

随机梯度下降是通过每个样本来迭代更新一次，如果样本量很大的情况（例如几十万），那么可能只用其中几万条或者几千条的样本，就已经将theta迭代到最优解了，对比上面的批量梯度下降，迭代一次需要用到十几万训练样本，一次迭代不可能最优，如果迭代10次的话就需要遍历训练样本10次。但是，SGD伴随的一个问题是噪音较BGD要多（高方差，如下图表示了SGD训练过程损失函数的变化），使得SGD并不是每次迭代都向着整体最优化方向，但大体方向是朝着最优解，SGD大约要遍历1-10次数据次来获取最优解。

代码是这样的：

for i in range(nb_epochs):
  np.random.shuffle(data)
  for example in data:
    params_grad = evaluate_gradient(loss_function, example, params)
    params = params - learning_rate * params_grad

基于上述两种算法的不足，诞生了一种折中的算法，即小批量梯度下降算法。

1.3 小批量梯度下降算法（Mini-batch Gradient Descent）

MBGD不像BGD每次用m（所有训练样本数）个examples去训练，也不像SGD每次用一个example。MBGD使用中间值b个examples 。经典的b取值大约在2-100 。MBGD算法如下：

代码实现：

for i in range(nb_epochs):
  np.random.shuffle(data)
  for batch in get_batches(data, batch_size=50):
    params_grad = evaluate_gradient(loss_function, batch, params)
    params = params - learning_rate * params_grad

从上述分析可以得出，MBGD优化算法的速度比BSD快，比SGD慢；精度比BSD低，比SGD高

 

2. 牛顿法和拟牛顿法

2.1 牛顿法（Newton's method）

（1）求函数的根

牛顿法的最初提出是用来求解方程的根的。我们假设点x∗为函数f(x)的根，那么有f(x∗)=0。现在我们把函数f(x)在点xk处一阶泰勒展开有：

那么假设点xk+1为该方程的根，则有

那么就可以得到

这样我们就得到了一个递归方程，我们可以通过迭代的方式不断的让x趋近于x∗从而求得方程f(x)的解。如下图所示：

（2）最优化

对于最优化问题，其极值点处有一个特性就是在极值点处函数的一阶导数为0。因此我们可以在一阶导数处利用牛顿法通过迭代的方式来求得最优解，即相当于求一阶导数对应函数的根。

首先，我们对函数在xk点处进行二阶泰勒展开：

因此，当x→xk时，f′(x)=f′(xk)+f′′(xk)(x−xk)。这里假设点xk+1是一阶导数的根，那么就有

可以得到：

这样我们就得到了一个不断更新x迭代求得最优解的方法。这个也很好理解，假设我们上面的第一张图的曲线表示的是函数f(x)一阶导数的曲线，那么其二阶导数就是一阶导数对应函数在某点的斜率，也就是那条切线的斜率，那么该公式就和上面求根的公式本质是一样的。 

特别地，对于高维函数（向量），其二阶导就变成了一个Hessian矩阵，记为H，那么迭代公式就变成了：

In summary，，牛顿法求解最优值的步骤如下：

• 随机选取起始点X0
• 计算目标函数f(x)在该点xk的一阶导数和海森矩阵； 
•  依据迭代公式更新x值 

如果E(f(xk+1)−f(xk))<ϵ，则收敛返回，否则继续步骤2,3直至收敛 

 

（3）牛顿法和梯度下降法比较

从本质上去看，牛顿法是二阶收敛，梯度下降是一阶收敛，所以牛顿法就更快。如果更通俗地说的话，比如你想找一条最短的路径走到一个盆地的最底部，梯度下降法每次只从你当前所处位置选一个坡度最大的方向走一步，牛顿法在选择方向时，不仅会考虑坡度是否够大，还会考虑你走了一步之后，坡度是否会变得更大。所以，可以说牛顿法比梯度下降法看得更远一点，能更快地走到最底部。（牛顿法目光更加长远，所以少走弯路；相对而言，梯度下降法只考虑了局部的最优，没有全局思想。）

牛顿法的优缺点总结：
　　优点：二阶收敛，收敛速度快；
　　缺点：牛顿法是一种迭代算法，每一步都需要求解目标函数的Hessian矩阵的逆矩阵，计算比较复杂

2.2 拟牛顿法（Quasi-Newton Methods）

基于上述对牛顿法的分析可知其在求解Hessian矩阵时计算量巨大，诞生了拟牛顿法。

拟牛顿法的本质思想是改善牛顿法每次需要求解复杂的Hessian矩阵的逆矩阵的缺陷，它使用正定矩阵来近似Hessian矩阵的逆，从而简化了运算的复杂度。

3. 共轭梯度法

共轭梯度法是介于最速下降法与牛顿法之间的一个方法，它仅需利用一阶导数信息，但克服了最速下降法收敛慢的缺点，又避免了牛顿法需要存储和计算Hesse矩阵并求逆的缺点，共轭梯度法不仅是解决大型线性方程组最有用的方法之一，也是解大型非线性最优化最有效的算法之一。 在各种优化算法中，共轭梯度法是非常重要的一种。其优点是所需存储量小，具有步收敛性，稳定性高，而且不需要任何外来参数。

具体原理及实现可参见Wikipedia：Conjugate gradient method

4. 启发式优化方法

启发式方法指人在解决问题时所采取的一种根据经验规则进行发现的方法。其特点是在解决问题时,利用过去的经验,选择已经行之有效的方法，而不是系统地、以确定的步骤去寻求答案。启发式优化方法种类繁多，包括经典的模拟退火方法、遗传算法、蚁群算法以及粒子群算法等等。还有一种特殊的优化算法被称之多目标优化算法，它主要针对同时优化多个目标（两个及两个以上）的优化问题，这方面比较经典的算法有NSGAII算法、MOEA/D算法以及人工免疫算法等。

占个坑，日后更新具体的几种启发式优化算法。嘻嘻

。。

。。

。。

5. 拉格朗日乘数法（Lagrange Multiplier Method）

作为一种优化算法，拉格朗日乘子法主要用于解决约束优化问题，它的基本思想就是通过引入拉格朗日乘子来将含有n个变量和k个约束条件的约束优化问题转化为含有（n+k）个变量的无约束优化问题。拉格朗日乘子背后的数学意义是其为约束方程梯度线性组合中每个向量的系数。

如何将一个含有n个变量和k个约束条件的约束优化问题转化为含有（n+k）个变量的无约束优化问题？拉格朗日乘数法从数学意义入手，通过引入拉格朗日乘子建立极值条件，对n个变量分别求偏导对应了n个方程，然后加上k个约束条件（对应k个拉格朗日乘子）一起构成包含了（n+k）变量的（n+k）个方程的方程组问题，这样就能根据求方程组的方法对其进行求解。

 

• 初始的约束问题：    min/max f(x,y,z)    s.t. g(x,y,z)=0
• 转化后的无约束问题（对偶问题）：  min/max [f(x,y,z) + λ g(x,y,z)]

至于为什么使用拉格朗日乘数法可以得到最优值，具体可参见Wikipedia：Lagrange multiplier

上面讨论的是等式约束条件下的优化问题，但是这并不足以描述人们面临的问题，不等式约束比等式约束更为常见。对于不等式问题，就需要用到KKT条件的拉格朗日乘数法。

 

首先，我们先介绍一下什么是KKT条件。KKT条件是指在满足一些有规则的条件下, 一个非线性规划(Nonlinear Programming)问题能有最优化解法的一个必要和充分条件. 这是一个广义化拉格朗日乘数的成果. 

求解的问题是：

定义不等式约束下的拉格朗日函数L为：

一般地, 一个最优化数学模型的列标准形式参考开头的式子, 所谓 Karush-Kuhn-Tucker 最优化条件，就是指上式的最优点x∗必须满足下面的条件:

1). 原约束条件：gi(x∗)≤0（i=1,2,…,p）以及,hj(x∗)=0（j=1,2,…,m）

2). 极值必要条件：L对X的一阶导数为零；

3). 互补松弛条件：λjhj(X)=0， j=1,2,…,m)

KKT条件第一项是说最优点x∗必须满足所有等式及不等式限制条件, 也就是说最优点必须是一个可行解, 这一点自然是毋庸置疑的. 第二项表明在最优点x∗, ∇f必须是∇gi和∇hj的线性組合, μi和λj都叫作拉格朗日乘子. 所不同的是不等式限制条件有方向性, 所以每一个λi都必须大于或等于零, 而等式限制条件没有方向性，所以uj没有符号的限制, 其符号要视等式限制条件的写法而定.

对于一般的任一问题而言，KKT条件是使一组解称为最优解的必要条件，当原问题是凸问题时，KKT条件也是充分条件。

参考：李航《统计学习方法》附录C

 

以上~

2018.05.15