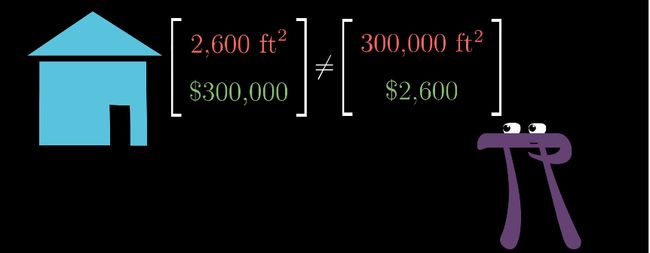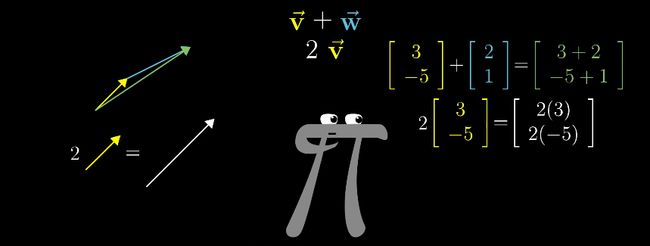向量是线性代数最基础、最基本的概念之一,要深入理解线性代数的本质,首先就要搞清楚向量到底是什么?
向量之所以让人迷糊,是因为我们在物理、数学,以及计算机等许多地方都见过它,但又没有彻底弄懂,以至于似是而非。
1. 物理学中的向量
物理学中的向量:空间中的箭头,由长度和它所指的方向决定
而且,在物理学中,你可以在空间中自由地移动向量,只要保持向量的长度和所指的方向不变,向量便保持不变,即移动前后的向量是同一个向量!
2. 计算机专业中的向量
计算机中向量是有序的列表
例如我们要对房价建模,
我们可以将房屋面积和房价排在一起形成向量,假定向量中的第 1 个元素用来表示房屋面积,第 2 个元素用来表示价格。显然,这是一个有序的列表,不能随意交换向量中元素的位置。
因此,站在计算机专业的角度来看,向量不过是列表或数组的别称罢了。
3. 数学中的向量
数学中的向量综合了不同专业对向量的理解。抽象意义上,数学中的向量可以是任意的东西,只要可以对它们进行加法和数乘运算即可。这也意味着,加法和数乘是向量最底层的运算。一切复杂和抽象的东西归根结底都源自于这 2 种运算。
和物理学中的向量一样,线性代数中的向量也是有大小和方向的(物理学观点),但必须特别注意的是:线性代数中的向量不能像物理学中的向量那样随意挪动。线性代数中的向量全部都是起点固定在原点的向量!
3.1 坐标
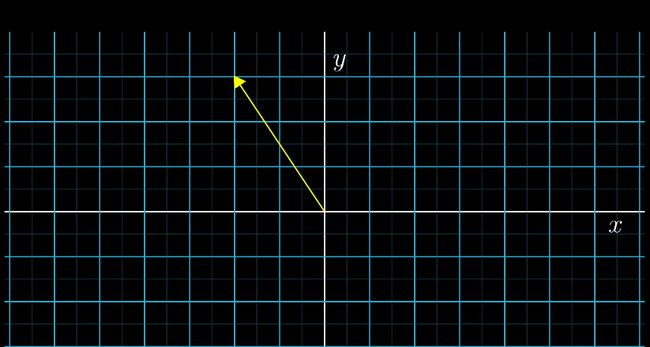
以大家最熟悉的二维平面直角坐标系为例,线性代数中,向量的坐标由一对数字构成。这一对数字指示了如何从向量的起点(即坐标原点)出发到达向量的终点。第 1 个数字 -2 告诉我们从原点出发沿 x 轴负方向移动 2 个单位的距离,第 2 个数字 3 告诉我们从原点出发沿 y 轴正方向移动 3 个单位的距离,然后我们就能到达向量的终点了。
显然,线性代数中的向量也是一个有序的列表(计算机观点)。例如,在上面的例子中,第 1 个数字表示从向量起点(原点)沿 x 轴移动的距离,第 2 个数字表示从向量起点(原点)沿 y 轴移动的距离,这 2 个数字当然是不能随意交换位置的。
为了将向量与坐标区分开来,我们通常将向量竖着写,而将坐标横着写。但无论如何,向量和坐标是有着一一对应的关系的。
3.2 向量加法
线性代数中向量的加法运算和物理学中向量的加法运算是一样的。
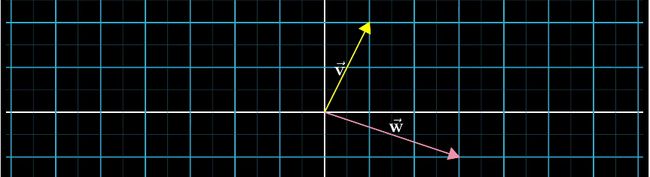
例如,要计算 v + w,
我们平移其中的任意一个向量(例如 w),将 w 的起点与 v 的终点重合,则平移后 w 的终点便是 v + w 的终点,而 v+ w 的起点也是 v 的起点(即原点)。前面,咪博士提到线性代数中的向量,都是起点固定在原点,不能随意挪动的。但是,在这里,我们却将向量 w 平移了。这确实是一个例外,而且可能也是线性代数中唯一允许向量离开原点的情形了。
但是,咪博士这里要讲的重点不是向量如何做加法运算,而是为什么向量的加法运算要定义成这样?
从刚才对坐标的解释,我们可以很自然地将向量看成是对某种运动的描述(从原点出发)。向量 v 和 w 分别描述了不同的运动, 向量加法想表达的意思是:v + w 描述的运动等价于 v 和 w 这 2 种运动综合的结果。即,v + w 描述的运动相当于先执行 v 描述的运动,再执行 w 描述的运动的结果。当然,你也可以先执行 w 的运动,再执行 v 的运动。最终结果都是一样的,无论向执行 v,还是先执行 w,最终都等于 v+ w 的运动。
这样理解起来比较抽象,咪博士还是为大家举一个具体的例子吧。
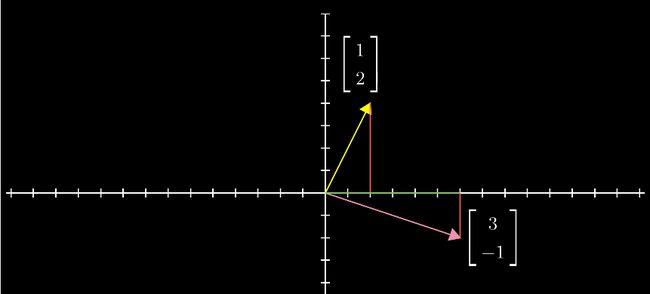
假定我们有 2 个向量 [ 1 2 ] 和 [3 -1] 。现在我们要对它们进行加法运算。
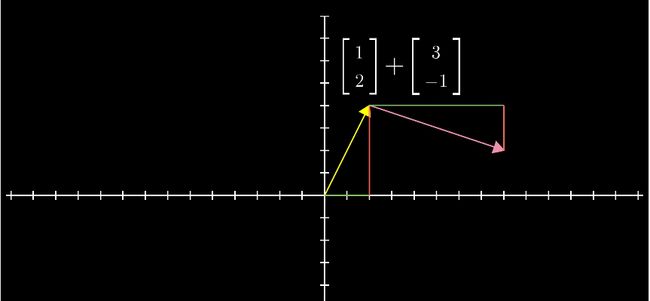
按照向量加法运算的计算方法,我们平移向量 [ 3 -1 ] ,让它的起点与向量 [ 1 2 ] 的终点重合。
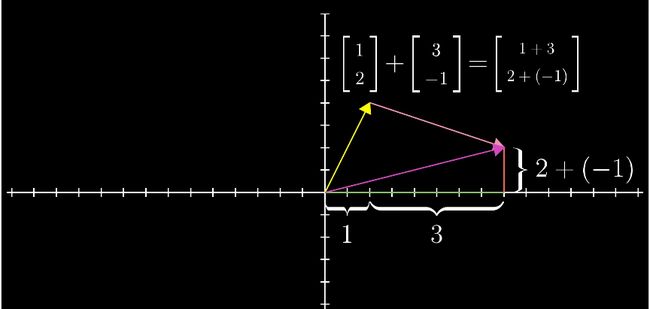
如果将向量看看成是某种形式的运动,那么 2 个向量相加就是相继执行向量对应的运动。最终向量相加的结果所表示的运动,就相当于,先沿 x 轴正方向移动 1 + 3 个单位,再沿 y 轴正方向移动 2 + (-1) 个单位。仔细想想,相加后的向量是不是恰好就是从原点出发,终点落在移动后的那个向量的终点上?
3.3 向量数乘
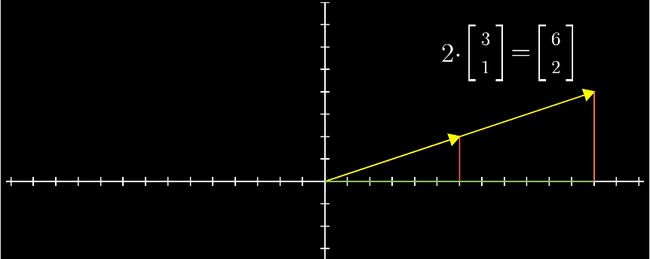
向量的数乘运算比加法运算要容易得多。向量的数乘运算就是对向量进行缩放,等于将向量中的各个元素(分量)分别进行缩放。现在,如果从向量坐标和运动的观点出发,是不是很容易理解了呢?
总之,要深入理解线性代数的本质,我们就需要学会灵活地在向量的不同解释之间相互转换。
原文链接:http://www.ipaomi.com/2017/11/17/线性代数的本质与几何意义-01-向量是什么?3blue1brown-咪博/