Spark MLlib中FPGrowth和FPTree详解之一
一、准备知识
1.1 Scala版本:2.10.4
1.2 Spark版本:1.5.0
Spark中实现关联规则算法的包是:org.apache.spark.mllib.fpm。包中的文件如下图所示:
这里面我重点讲解红色箭头指向的两个代码文件。讲解过程中如果有误解的地方,还请评论指正,谢谢!
1.3 频繁模式增长FP-Growth
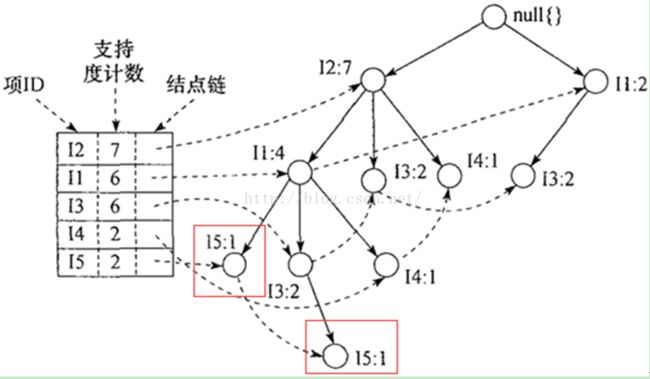
要理解Spark MLlib中FPGrowth和FPTree中的源码,首先在理论上要有一定的基础。首先就是韩教授他们发明的基于频繁模式树的关联规则挖掘算法。这里就不细表了,只要记得如下图的频繁模式树的原理就行。友情提醒:结点链和叶子结点对理解源码很有帮助
注:摘自韩家炜《数据挖掘》
图中的数据样本也是我们等下理解源码进行测试的数据样本,样本如下表所示
测试样本
| TID |
商品ID的列表 |
| T100 |
I1,I2,I5 |
| T200 |
I2,I4 |
| T300 |
I2,I3 |
| T400 |
I1,I2,I4 |
| T500 |
I1,I3 |
| T600 |
I2,I3 |
| T700 |
I1,I3 |
| T800 |
I1,I2,I3,I5 |
| T900 |
I1,I2,I3 |
1.4 并行频繁模式增长PFP-Growth
Spark MLlib中的FPGrowth一个并行化的版本实现,在其注释中也提到了实现算法的出处。摘录如下,红色字体为文献标题。
/**
*
* Aparallel FP-growth algorithm to mine frequent itemsets. The algorithm isdescribed in
*[[http://dx.doi.org/10.1145/1454008.1454027 Li et al., PFP: Parallel FP-Growth for Query
* Recommendation]].PFP distributes computation in such a way that each worker executes an
*independent group of mining tasks. The FP-Growth algorithm is described in
*[[http://dx.doi.org/10.1145/335191.335372 Han et al., Mining frequent patternswithout candidate
* generation]].
*
*@param minSupport the minimal support level of the frequent pattern, anypattern appears
* more than (minSupport *size-of-the-dataset) times will be output
*@param numPartitions number of partitions used by parallel FP-growth
*
*@see [[http://en.wikipedia.org/wiki/Association_rule_learning Association rulelearning
* (Wikipedia)]]
*
*/
所以在开始阅读源码之前,最好还是先读几遍相关的文献。在下面的章节中,我会以刚才的样本为例,演示一下PFP的过程,如果读过该文献,理解起来应该还是容易的。因为文献是英文,这里大致讲解一下过程:
以样本数据集为例,其运行过程如下所示:
| TID |
商品ID的列表 |
排序后的ID与对应组ID |
基于Q对事务进行划分 |
| T100 |
I1,I2,I5 |
I2, I1, I5 -> Q1, Q1, Q3 |
Q3->{I2, I1, I5 }, Q1->{I2, I1} |
| T200 |
I2,I4 |
I2, I4 -> Q1, Q2 |
Q2->{I2, I4}, Q1->{I2} |
| T300 |
I2,I3 |
I2, I3 -> Q1, Q2 |
Q2->{I2, I3}, Q1->{I2} |
| T400 |
I1,I2,I4 |
I2, I1, I4 -> Q1, Q1, Q2 |
Q2->{I2, I1, I4}, Q1->{I2, I1} |
| T500 |
I1,I3 |
I1, I3 -> Q1, Q2 |
Q2->{I1, I3}, Q1->{I1} |
| T600 |
I2,I3 |
I2, I3 -> Q1, Q2 |
Q2->{I2, I3}, Q1->{I2} |
| T700 |
I1,I3 |
I1, I3 -> Q1, Q2 |
Q2->{I1, I3}, Q1->{I1} |
| T800 |
I1,I2,I3,I5 |
I2, I1, I3, I5 -> Q1, Q1, Q2,Q3 |
Q3->{I2, I1,I3, I5 }, Q2->{I2,I1,I3}, Q1->{I2, I1} |
| T900 |
I1,I2,I3 |
I2, I1, I3 -> Q1, Q1, Q2 |
Q2->{I2,I1,I3}, Q1->{I2, I1} |
| F-list |
I2:7 I1:6 I3:6 I4:2 I5:2 |
||
| Q-list |
Q1:{I2, I1} Q2:{I3, I4} Q3:{I5} |
||
二、源码详解
2.1 首先给出这两个代码文件的概览,如下表所示,对源码进行的分解说明。
FPGrowth和FPTree源码概览
2.2 FPTree源码详解
FPTree.scala中定义了FPTree类和它的单例对象。
而在单例对象中又定义了两个类。一个是Node类,顾名思义,就是表示树上的结点。具体的说明见下面的注释
/**
* Representing a node in an FP-Tree.
* @paramparent该结点的父结点
*/
class Node[T](valparent: Node[T])extends Serializable {
var item: T = _ //结点中包含的项(商品)
var count: Long = 0L //对应的计数
/**
* children表示孩子结点,用一个item->Node[item]的映射表示
* 根据FPTree的特点,一个结点的孩子结点中包含的项item肯定是互不相同的;
* 或者一个item在树的每一层最多只能出现一次,在树的每个分枝也只可能出现一次
*/
val children: mutable.Map[T, Node[T]] = mutable.Map.empty
def isRoot: Boolean =parent ==null//判断是否到达根结点
}
这里要注意的是不同的Node可以由相同的item构成,比如下图中框出来存在于不同分枝的I5结点。而连接这两个Node的虚线其实就是接下来要介绍的另一个类Summary。
包含相同item的不同Nodes
Summary是单例对象中另一个类,其注释如下:
/**
* Summary of a item in an FP-Tree.
* 就是同一个项item对应的结点链
*/
private class Summary[T] extendsSerializable {
var count: Long = 0L //item(商品)在数据样本(transactions)中出现的次数
val nodes: ListBuffer[Node[T]] = ListBuffer.empty //FPTree中包该item的所有结点列表
}
理解了这两个类之后,我们再来看FPTree这个关键类。
首先类成员变量包括一个root和summaries. Summaries定义如下,是所有item到它的结点链的映射。
private val summaries: mutable.Map[T, Summary[T]] = mutable.Map.empty
下图中的列表是比较形象的理解。
Summaries的形象化理解
接下来的一些方法,这里只给出一些注释,具体的运行过程在测试样本(第二章)的时候再讲解。
/** Adds a transaction withcount. */
def add(t: Iterable[T], count: Long =1L):this.type = {
require(count > 0)
var curr = root //从根结点开始,将事务中的项依次添加到当前结点的孩子结点中
curr.count += count
/**
* 可以将一个transaction看作树的一个分枝
* 接下来就是将这个分枝添加到树中,对应层上有包含相同item的Node时就只更新count
* 没有就要生成新的结点。。。
*/
t.foreach { item => //依次遍历事务中的每一项
val summary = summaries.getOrElseUpdate(item,new Summary)//如果item在树中已经存在,获取其结点链,否则生成一个
summary.count += count
val child = curr.children.getOrElseUpdate(item,{//首先从当前结点的孩子结点中看item是否存在
val newNode = new Node(curr) //如果不存在,生成一个新的以curr为父结点的newNode
newNode.item = item
summary.nodes +=newNode
newNode
})
child.count += count
curr = child //得到孩子结点之后,将孩子结点看作当前结点向下遍历
}//foreach过程执行结束
this
}
/**
* Gets a subtree with the suffix.
* 以事务中某项item为后缀,向上遍历FPTree
* 得到一颗以包含item的Node为叶子结点的子树
* 但是该方法是从item的父结点开始的,所以子树中不包含item
* 这是因为extract方法中递归提取的原因
*/
private def project(suffix: T): FPTree[T] = {
val tree = new FPTree[T]
if (summaries.contains(suffix)) {//判断结点链中是否包含该后缀项(貌似没有必要)
val summary = summaries(suffix) //获取该suffix对应的结点链
summary.nodes.foreach { node =>
var t = List.empty[T]
var curr = node.parent //从父结点开始
while (!curr.isRoot) {//一直向上遍历直到根结点
t = curr.item :: t
curr = curr.parent
}
//t中是一条以item为结点的分枝
tree.add(t, node.count)
}
}
tree
}
举个例子,假设item=I5,I5对应的summary中包含两个结点。Project方法分别从这两个结点向上遍历,遍历过程如下图所示。
以I5为后缀的子树投影过程
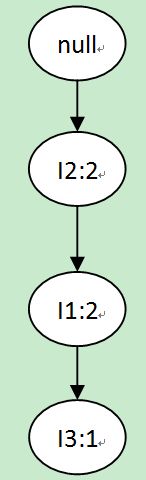
遍历之后,就可以得到下图所示子树:
Project(I5)方法的输出
/**
* Extracts allpatterns with valid suffix and minimum count.
* 分别以summaries一个item为后缀,递归输出所有的频繁项
*/
def extract(
minCount: Long,
validateSuffix: T => Boolean = _ =>true): Iterator[(List[T], Long)] = {
summaries.iterator.flatMap {case (item,summary) =>//每一项和它对应结点链
/**
* validateSuffix只在第一次进行判断,判断该item是否属于FPTree对应的分区part
* 在FPGrowth的genFreqItemSets方法中,可以看到一行代码 tree.extract(minCount, x=> partitioner.getPartition(x) == part)
* PFP算法中将所有item进行组划分,假设有3组。那么每个item都有一个组号,在spark中是分区号。
* 另外,每组都对应着一颗FPTree,对每一组的FPTree提取频繁模式的时候,
* 只能以属于该组的那些项items为后缀来提取,不属于该分区的则忽略
* 但是提取过程中是不需要再判断的
*/
if (validateSuffix(item) &&summary.count >= minCount) {//
Iterator.single((item :: Nil,summary.count)) ++//单item为频繁一项集中的一个
project(item).extract(minCount).map{case (t,c) =>//递归的抽取item所在分枝上所有大于minCount的项集
(item :: t, c)
}
} else {
Iterator.empty
}
}
}未完待续……