【CODE】二分查找 && 二维矩阵问题 && 螺旋矩阵 && 中位数
目录
475. Heaters
441. Arranging Coins
363. Max Sum of Rectangle No Larger Than K
240. Search a 2D Matrix II
74. Search a 2D Matrix
54. Spiral Matrix
59. Spiral Matrix II
73. Set Matrix Zeroes
289. Game of Life
329. Longest Increasing Path in a Matrix
221. Maximal Square
84. Largest Rectangle in Histogram
85. Maximal Rectangle
4. Median of Two Sorted Arrays
295. Find Median from Data Stream
475. Heaters
Easy
619678Add to ListShare
Winter is coming! Your first job during the contest is to design a standard heater with fixed warm radius to warm all the houses.
Now, you are given positions of houses and heaters on a horizontal line, find out minimum radius of heaters so that all houses could be covered by those heaters.
So, your input will be the positions of houses and heaters seperately, and your expected output will be the minimum radius standard of heaters.
Note:
- Numbers of houses and heaters you are given are non-negative and will not exceed 25000.
- Positions of houses and heaters you are given are non-negative and will not exceed 10^9.
- As long as a house is in the heaters' warm radius range, it can be warmed.
- All the heaters follow your radius standard and the warm radius will the same.
Example 1:
Input: [1,2,3],[2] Output: 1 Explanation: The only heater was placed in the position 2, and if we use the radius 1 standard, then all the houses can be warmed.
Example 2:
Input: [1,2,3,4],[1,4] Output: 1 Explanation: The two heater was placed in the position 1 and 4. We need to use radius 1 standard, then all the houses can be warmed.
#include"pch.h"
#include
#include
#include
#include
using namespace std;
int findRadius(vector& houses, vector& heaters) {
sort(houses.begin(), houses.end());
sort(heaters.begin(), heaters.end());
for (int i = 0; i < houses.size(); i++) cout << houses[i] << " ";
cout << endl;
for (int j = 0; j < heaters.size(); j++) cout << heaters[j] << " ";
cout << endl;
int max = 0;
for (int i = 0; i < houses.size(); i++) {
//找第一个大于等于houses[i]的heaters
int dis = lower_bound(heaters.begin(), heaters.end(), houses[i])- heaters.begin();
cout << dis << " ";
if (dis >= heaters.size()) dis = heaters.size() - 1;
if (dis == 0) max = max > abs(heaters[dis] - houses[i]) ? max : abs(heaters[dis] - houses[i]);
else {
int n1 = abs(heaters[dis] - houses[i]);
int n2 = abs(heaters[dis - 1] - houses[i]);
n1 = n1 < n2 ? n1 : n2;
max = max > n1 ? max : n1;
}
}
return max;
}
int main() {
vector houses = { 282475249,622650073,984943658,458777923 };
vector heaters = {823564440,115438165,16531729,823378840,143542612};
cout << findRadius(houses, heaters);
return 0;
} class Solution {
public:
int findRadius(vector& houses, vector& heaters) {
sort(houses.begin(),houses.end());
sort(heaters.begin(),heaters.end());
int i=0,j=0,max=0;
for(i=0;i0 && jn1?max:n1;
}else if(j==0){
int n1=abs(houses[i]-heaters[j]);
max=max>n1?max:n1;
}else if(j==heaters.size()){
int n1=abs(houses[i]-heaters[j-1]);
max=max>n1?max:n1;
}
}
return max;
}
}; 441. Arranging Coins
Easy
265565Add to ListShare
You have a total of n coins that you want to form in a staircase shape, where every k-th row must have exactly k coins.
Given n, find the total number of full staircase rows that can be formed.
n is a non-negative integer and fits within the range of a 32-bit signed integer.
Example 1:
n = 5 The coins can form the following rows: ¤ ¤ ¤ ¤ ¤ Because the 3rd row is incomplete, we return 2.
Example 2:
n = 8 The coins can form the following rows: ¤ ¤ ¤ ¤ ¤ ¤ ¤ ¤ Because the 4th row is incomplete, we return 3.
class Solution {
public:
int arrangeCoins(int n) {
/*Runtime: 4 ms, faster than 86.52% of C++ online submissions for Arranging Coins.
Memory Usage: 7.4 MB, less than 100.00% of C++ online submissions for Arranging Coins.
if(n==0) return 0;
vector arr;
int now=1,i=1;
long long next=1;
for(i=2;i<=n;i++){
next+=i;
if(now<=n && next>n) return i-1;
}
return 1;*/
/*二分查找,lgn
Runtime: 4 ms, faster than 86.52% of C++ online submissions for Arranging Coins.
Memory Usage: 7.2 MB, less than 100.00% of C++ online submissions for Arranging Coins.*/
long long left=1,right=n;
while(left<=right){
long long mid=left+(right-left)/2;
long long tmp;
tmp=(mid+1)*mid/2;
if(tmp>n) right=mid-1;
else if(tmp==n) return mid;
else left=mid+1;
}
return right;
}
}; 363. Max Sum of Rectangle No Larger Than K
Hard
62842Add to ListShare
Given a non-empty 2D matrix matrix and an integer k, find the max sum of a rectangle in the matrix such that its sum is no larger than k.
Example:
Input: matrix = [[1,0,1],[0,-2,3]], k = 2 Output: 2 Explanation: Because the sum of rectangle [[0, 1], [-2, 3]] is 2,and 2 is the max number no larger than k (k = 2).
Note:
- The rectangle inside the matrix must have an area > 0.
- What if the number of rows is much larger than the number of columns?
#include"pch.h"
#include
#include
#include
#include
using namespace std;
/*363. Max Sum of Rectangle No Larger Than K
1.计算每个矩阵的和
Runtime: 1060 ms, faster than 17.91% of C++ online submissions for Max Sum of Rectangle No Larger Than K.
Memory Usage: 9.9 MB, less than 100.00% of C++ online submissions for Max Sum of Rectangle No Larger Than K.*/
int maxSumSubmatrix1(vector>& matrix, int k) {
int n = matrix.size(), m = matrix[0].size();
int max = INT_MIN;
vector > sum(n + 1, vector(m + 1));
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
sum[i][j] = sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1] + matrix[i - 1][j - 1];
if (sum[i][j] <= k && max < sum[i][j]) max = sum[i][j];
if (max == k) return max;
}
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
for (int q = 1; q <= i; q++) {
for (int l = 1; l <= j; l++) {
int tmp = sum[i][j] - sum[i][l - 1] - sum[q - 1][j] + sum[q - 1][l - 1];
if (tmp <= k && max < tmp) max = tmp;
if (max == k) return max;
}
}
}
}
return max;
}
/*2.基于计算二维数组中最大子矩阵和算法
将二维数组按行或列拆分成多个一维数组,然后利用一维数组的累加和来找到符合要求的数字
使用lower_bound加快搜索速度,或者使用二分搜索代替
要先放一个0进去,这样找lower_bound(curSum-k),当curSum=k时,就可以返回0了
Runtime: 412 ms, faster than 38.34% of C++ online submissions for Max Sum of Rectangle No Larger Than K.
Memory Usage: 99.8 MB, less than 58.82% of C++ online submissions for Max Sum of Rectangle No Larger Than K.*/
int maxSumSubmatrix(vector>& matrix, int k) {
if (matrix.empty() || matrix[0].empty()) return 0;
int m = matrix.size(), n = matrix[0].size(), res = INT_MIN;
for (int i = 0; i < n; ++i) {//遍历各列
vector sum(m);
for (int j = i; j < n; ++j) {//对于第i到第n-1列
for (int k = 0; k < m; ++k) {//累加各行
sum[k] += matrix[k][j];
}
//sum[k]每轮表示:第i列,第i到i+1列,第i到i+2列,从第0到第k行的和
//就是[0][i]->[k][i+x]的矩阵和
int curSum = 0;
set st{ {0} };
for(int k=0;k[k][j]的矩阵和
auto it = st.lower_bound(curSum - k);
//在set中找第一个≥curSum-k的数字,*it
//*it≥curSum-k,curSum-*it≤k,*it是之前存入的比现在这个面积小的矩阵的和
if (it != st.end()) res = max(res, curSum - *it);
//如果*it是第一个≥curSum-k的数字,curSum-*it≤k,说明这个和是符合条件的,更新res
st.insert(curSum);
//将当前矩阵和加入set
}
}
}
return res;
} 240. Search a 2D Matrix II
Medium
244667Add to ListShare
Write an efficient algorithm that searches for a value in an m x n matrix. This matrix has the following properties:
- Integers in each row are sorted in ascending from left to right.
- Integers in each column are sorted in ascending from top to bottom.
Example:
Consider the following matrix:
[ [1, 4, 7, 11, 15], [2, 5, 8, 12, 19], [3, 6, 9, 16, 22], [10, 13, 14, 17, 24], [18, 21, 23, 26, 30] ]
Given target = 5, return true.
Given target = 20, return false.
#include"pch.h"
#include
#include
#include
#include
using namespace std;
/*240. Search a 2D Matrix II
Runtime: 56 ms, faster than 98.18% of C++ online submissions for Search a 2D Matrix II.
Memory Usage: 12 MB, less than 100.00% of C++ online submissions for Search a 2D Matrix II.*/
bool searchMatrix(vector>& matrix, int target) {
if (matrix.size() == 0) return false;
int n = matrix.size(), m = matrix[0].size();
int i = n - 1, j = 0;
while (i >= 0 && j < m) {
if (matrix[i][j] < target) j++;
else if (matrix[i][j] > target) i--;
else if (matrix[i][j] == target) return true;
}
return false;
} https://blog.csdn.net/Li_Jiaqian/article/details/104497704#378.%C2%A0Kth%20Smallest%20Element%20in%20a%20Sorted%20Matrix
74. Search a 2D Matrix
Medium
1341141Add to ListShare
Write an efficient algorithm that searches for a value in an m x n matrix. This matrix has the following properties:
- Integers in each row are sorted from left to right.
- The first integer of each row is greater than the last integer of the previous row.
Example 1:
Input: matrix = [ [1, 3, 5, 7], [10, 11, 16, 20], [23, 30, 34, 50] ] target = 3 Output: true
Example 2:
Input: matrix = [ [1, 3, 5, 7], [10, 11, 16, 20], [23, 30, 34, 50] ] target = 13 Output: false
#include"pch.h"
#include
#include
#include
#include
using namespace std;
/*74. Search a 2D Matrix
在第一列中,找第一个大于等于目标值的,确定行数
在该行再用二分查找进行查找
Runtime: 8 ms, faster than 94.75% of C++ online submissions for Search a 2D Matrix.
Memory Usage: 8.8 MB, less than 100.00% of C++ online submissions for Search a 2D Matrix.*/
bool searchMatrix(vector>& matrix, int target) {
if (matrix.size() == 0) return false;
int n = matrix.size(), m = matrix[0].size();
if (m == 0) return false;
int up = 0, down = n - 1;
while (up <= down) {
int mid = up + (down - up) / 2;
if (matrix[mid][0] < target) up = mid + 1;
else if (matrix[mid][0] > target) down = mid - 1;
else return true;
}
down = down < 0 ? 0 : down;
int left = 0, right = m - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (matrix[down][mid] < target) left = mid + 1;
else if (matrix[down][mid] > target) right = mid - 1;
else return true;
}
return false;
} 54. Spiral Matrix
Medium
1798498Add to ListShare
Given a matrix of m x n elements (m rows, n columns), return all elements of the matrix in spiral order.
Example 1:
Input: [ [ 1, 2, 3 ], [ 4, 5, 6 ], [ 7, 8, 9 ] ] Output: [1,2,3,6,9,8,7,4,5]
Example 2:
Input: [ [1, 2, 3, 4], [5, 6, 7, 8], [9,10,11,12] ] Output: [1,2,3,4,8,12,11,10,9,5,6,7]
class Solution {
public:
/*Runtime: 0 ms, faster than 100.00% of C++ online submissions for Spiral Matrix.
Memory Usage: 8 MB, less than 100.00% of C++ online submissions for Spiral Matrix.*/
vector spiralOrder(vector>& matrix) {
vector res;
if(matrix.size()==0) return res;
if(matrix[0].size()==0) return res;
int n=matrix.size()-1,m=matrix[0].size()-1;
int i=0,j=0,up=1,left=0;
res.push_back(matrix[0][0]);
while(res.size()!=matrix.size()*matrix[0].size()){
while(jleft) res.push_back(matrix[i][--j]);
if(res.size()==matrix.size()*matrix[0].size()) break;
left++;
while(i>up) res.push_back(matrix[--i][j]);
if(res.size()==matrix.size()*matrix[0].size()) break;
up++;
}
return res;
}
}; class Solution {
public:
/*Runtime: 0 ms, faster than 100.00% of C++ online submissions for Spiral Matrix.
Memory Usage: 7.7 MB, less than 100.00% of C++ online submissions for Spiral Matrix.*/
vector spiralOrder(vector>& matrix) {
vector res;
if(matrix.size()==0) return res;
if(matrix[0].size()==0) return res;
int n=matrix.size(),m=matrix[0].size();
int left=0,right=m-1,up=0,down=n-1;
while(true){
for(int i=left;i<=right;i++) res.push_back(matrix[up][i]);
if(++up>down) break;
for(int i=up;i<=down;i++) res.push_back(matrix[i][right]);
if(--right=left;i--) res.push_back(matrix[down][i]);
if(--down=up;i--) res.push_back(matrix[i][left]);
if(++left>right) break;
}
return res;
}
}; - 第二种方法,设置4个上下限坐标会好看一些
59. Spiral Matrix II
Medium
778101Add to ListShare
Given a positive integer n, generate a square matrix filled with elements from 1 to n2 in spiral order.
Example:
Input: 3 Output: [ [ 1, 2, 3 ], [ 8, 9, 4 ], [ 7, 6, 5 ] ]
class Solution {
public:
/*Runtime: 4 ms, faster than 74.26% of C++ online submissions for Spiral Matrix II.
Memory Usage: 7.9 MB, less than 100.00% of C++ online submissions for Spiral Matrix II.*/
vector> generateMatrix(int n) {
vector > res(n,vector(n));
int num=1;
int left=0,right=n-1,up=0,down=n-1;
while(true){
for(int j=left;j<=right;j++) res[up][j]=num++;
if(++up>down) break;
for(int i=up;i<=down;i++) res[i][right]=num++;
if(--right=left;j--) res[down][j]=num++;
if(--down=up;i--) res[i][left]=num++;
if(++left>right) break;
}
return res;
}
}; 73. Set Matrix Zeroes
Medium
1616271Add to ListShare
Given a m x n matrix, if an element is 0, set its entire row and column to 0. Do it in-place.
Example 1:
Input: [ [1,1,1], [1,0,1], [1,1,1] ] Output: [ [1,0,1], [0,0,0], [1,0,1] ]
Example 2:
Input: [ [0,1,2,0], [3,4,5,2], [1,3,1,5] ] Output: [ [0,0,0,0], [0,4,5,0], [0,3,1,0] ]
Follow up:
- A straight forward solution using O(mn) space is probably a bad idea.
- A simple improvement uses O(m + n) space, but still not the best solution.
- Could you devise a constant space solution?
class Solution {
public:
/*使用set记录含有0的行数和列数
Runtime: 40 ms, faster than 99.05% of C++ online submissions for Set Matrix Zeroes.
Memory Usage: 10.6 MB, less than 100.00% of C++ online submissions for Set Matrix Zeroes.*/
void setZeroes(vector>& matrix) {
int n=matrix.size();
if(n==0) return;
int m=matrix[0].size();
if(m==0) return;
set hang,lie;
for(int i=0;i class Solution {
public:
/*O(1)
Runtime: 44 ms, faster than 92.86% of C++ online submissions for Set Matrix Zeroes.
Memory Usage: 10.3 MB, less than 100.00% of C++ online submissions for Set Matrix Zeroes.*/
void setZeroes(vector>& matrix) {
int n=matrix.size();
if(n==0) return;
int m=matrix[0].size();
if(m==0) return;
bool hang=false,lie=false;
for(int j=0;j 289. Game of Life
Medium
1443245Add to ListShare
According to the Wikipedia's article: "The Game of Life, also known simply as Life, is a cellular automaton devised by the British mathematician John Horton Conway in 1970."
Given a board with m by n cells, each cell has an initial state live (1) or dead (0). Each cell interacts with its eight neighbors (horizontal, vertical, diagonal) using the following four rules (taken from the above Wikipedia article):
- Any live cell with fewer than two live neighbors dies, as if caused by under-population.
- Any live cell with two or three live neighbors lives on to the next generation.
- Any live cell with more than three live neighbors dies, as if by over-population..
- Any dead cell with exactly three live neighbors becomes a live cell, as if by reproduction.
Write a function to compute the next state (after one update) of the board given its current state. The next state is created by applying the above rules simultaneously to every cell in the current state, where births and deaths occur simultaneously.
Example:
Input: [ [0,1,0], [0,0,1], [1,1,1], [0,0,0] ] Output: [ [0,0,0], [1,0,1], [0,1,1], [0,1,0] ]
Follow up:
- Could you solve it in-place? Remember that the board needs to be updated at the same time: You cannot update some cells first and then use their updated values to update other cells.
- In this question, we represent the board using a 2D array. In principle, the board is infinite, which would cause problems when the active area encroaches the border of the array. How would you address these problems?
-
康威生命游戏, 一种细胞自动机,每一个位置有两种状态,1为活细胞,0为死细胞,对于每个位置都满足如下的条件:
-
1. 如果活细胞周围八个位置的活细胞数少于两个,则该位置活细胞死亡
-
2. 如果活细胞周围八个位置有两个或三个活细胞,则该位置活细胞仍然存活
-
3. 如果活细胞周围八个位置有超过三个活细胞,则该位置活细胞死亡
-
4. 如果死细胞周围正好有三个活细胞,则该位置死细胞复活
-
当一个位置更新了,这个位置成为其他位置的 neighbor 时,怎么知道其未更新的状态呢?可以使用状态机转换:
-
状态转换:
-
状态0:死->死,状态1:活->活,状态2:活->死,状态3:死->活
-
最后状态更新完后,统一 mod 2
-
判断的是邻居转换前的状态:0、3是死,1、2是活
-
自己是活的 && 2/3个邻居是活的 -> 下一代是活的,否则是死的
-
自己是死的 && 3个邻居是活的 -> 下一代是活的,否则是死的
-
最后对所有状态对2取余,则状态0和2就变成死细胞,状态1和3就是活细胞,达成目的。先对原数组进行逐个扫描,对于每一个位置,扫描其周围八个位置,如果遇到状态1或2,就计数器累加1,扫完8个邻居,如果少于两个活细胞或者大于三个活细胞,而且当前位置是活细胞的话,标记状态2,如果正好有三个活细胞且当前是死细胞的话,标记状态3。完成一遍扫描后再对数据扫描一遍,对2取余变成我们想要的结果。
class Solution {
public:
/*状态转换:
状态0:死->死,状态1:活->活,状态2:活->死,状态3:死->活
最后状态更新完后,统一 mod 2
判断的是邻居转换前的状态:0、3是死,1、2是活
自己是活的 && 2/3个邻居是活的 -> 下一代是活的,否则是死的
自己是死的 && 3个邻居是活的 -> 下一代是活的,否则是死的
Runtime: 0 ms, faster than 100.00% of C++ online submissions for Game of Life.
Memory Usage: 7.8 MB, less than 100.00% of C++ online submissions for Game of Life.*/
void gameOfLife(vector>& board) {
int n=board.size();
if(n==0) return ;
int m=board[0].size();
if(m==0) return;
int dx[8]={-1,-1,-1,0,0,1,1,1};
int dy[8]={-1,0,1,-1,1,-1,0,1};
for(int i=0;i=0 && x=0 && y3){//已经超过3个活邻居了
break;
}
}
if(board[i][j]==1){
if(huo==2 || huo==3) board[i][j]=1;//状态1:活->活
else board[i][j]=2;//状态2:活->死
}
else if(board[i][j]==0){
if(huo==3) board[i][j]=3;//状态3:死->活
else board[i][j]=0;//状态0:死->死,
}
}
}
for(int i=0;i 329. Longest Increasing Path in a Matrix
Given an integer matrix, find the length of the longest increasing path.
From each cell, you can either move to four directions: left, right, up or down. You may NOT move diagonally or move outside of the boundary (i.e. wrap-around is not allowed).
Example 1:
Input: nums = [ [9,9,4], [6,6,8], [2,1,1] ] Output: 4 Explanation: The longest increasing path is [1, 2, 6, 9].
Example 2:
Input: nums = [ [3,4,5], [3,2,6], [2,2,1] ] Output: 4 Explanation: The longest increasing path is [3, 4, 5, 6] . Moving diagonally is not allowed.
#include"pch.h"
#include
#include
#include
#include
#include
using namespace std;
/*329. Longest Increasing Path in a Matrix
1.DFS,超时*/
void DFS1(vector>& matrix,int x,int y,vector > &vis,int &max,int len,int last) {
if (x < 0 || y < 0 || x >= matrix.size() || y >= matrix[0].size() || vis[x][y]==1) return;
if (last < matrix[x][y]) {
len++;
max = max > len ? max : len;
vis[x][y] = 1;
DFS1(matrix, x - 1, y, vis, max, len, matrix[x][y]);
DFS1(matrix, x, y - 1, vis, max, len, matrix[x][y]);
DFS1(matrix, x + 1, y, vis, max, len, matrix[x][y]);
DFS1(matrix, x, y + 1, vis, max, len, matrix[x][y]);
vis[x][y] = 0;
}
return;
}
int longestIncreasingPath1(vector>& matrix) {
if (matrix.size() == 0) return 0;
if (matrix[0].size() == 0) return 0;
vector > vis(matrix.size(), vector(matrix[0].size()));
int max = 0;
for (int i = 0; i < matrix.size(); i++) {
for (int j = 0; j < matrix[0].size(); j++) {
DFS1(matrix, i, j, vis, max, 0, INT_MIN);
}
}
return max;
}
/*2.dp,dp[i][j]表示从(i,j)出发,最长距离
Runtime: 36 ms, faster than 92.93% of C++ online submissions for Longest Increasing Path in a Matrix.
Memory Usage: 11.8 MB, less than 100.00% of C++ online submissions for Longest Increasing Path in a Matrix.*/
int dir[4][2] = { {0,-1},{-1,0},{0,1},{1,0} };
int DFS2(vector > &matrix, vector > &dp, int i, int j) {
if (dp[i][j]) return dp[i][j];
int mx = 1, m = matrix.size(), n = matrix[0].size();
for (auto a : dir) {
int x = i + a[0], y = j + a[1];
if (x < 0 || x >= m || y < 0 || y >= n || matrix[x][y] >= matrix[i][j]) continue;
int len = 1 + DFS2(matrix, dp, x, y);
mx = max(mx, len);
}
dp[i][j] = mx;
return mx;
}
int longestIncreasingPath(vector>& matrix) {
if (matrix.size() == 0) return 0;
if (matrix[0].size() == 0) return 0;
vector > dp(matrix.size(), vector(matrix[0].size()));
int maxx = 0;
for (int i = 0; i < matrix.size(); i++) {
for (int j = 0; j < matrix[0].size(); j++) {
maxx = max(maxx,DFS2(matrix, dp, i, j));
}
}
return maxx;
}
int main() {
vector > matrix = { {9,9,4},{6,6,8},{2,1,1} };
cout << longestIncreasingPath(matrix);
return 0;
} 221. Maximal Square
Given a 2D binary matrix filled with 0's and 1's, find the largest square containing only 1's and return its area.
Example:
Input:
1 0 1 0 0
1 0 1 1 1
1 1 1 1 1
1 0 0 1 0
Output: 4
#include"pch.h"
#include
#include
#include
#include
#include
using namespace std;
/*221. Maximal Square
1.遍历每个点,以每个点为左上角,找正方形
Runtime: 16 ms, faster than 95.92% of C++ online submissions for Maximal Square.
Memory Usage: 9.8 MB, less than 100.00% of C++ online submissions for Maximal Square.*/
void DFS(vector>& matrix, int i, int j, int &maxx) {
int lenmax = min(matrix.size() - i, matrix[0].size() - j);//正方形最大边长
if (lenmax < maxx) return;//最大边长小于当前最大值,直接跳出
int flag = 0, tmpmax = 0;
for (int l = 2; l <= lenmax && flag == 0; l++) {//边长l,从1遍历到lenmax
//每次新增的正方形,在前一个的基础上,只需要遍历最外面的两个边就可以了
for (int a = i; a < i + l && flag == 0; a++) {//新增列:j+l-1,遍历新增列
if (matrix[a][j + l - 1] == '0') flag = 1;
}
for (int b = j; b < j + l && flag == 0; b++) {//新增行:i+l-1,遍历新增行
if (matrix[i + l - 1][b] == '0') flag = 1;
}
if (flag == 0) tmpmax = l;
}
if (tmpmax > maxx) maxx = tmpmax;
return;
}
int maximalSquare1(vector>& matrix) {
int maxx = 1, one = 0;
for (int i = 0; i < matrix.size(); i++) {
for (int j = 0; j < matrix[0].size(); j++) {
if (matrix[i][j] != '0') {
one++;
DFS(matrix, i, j, maxx);
}
}
}
if (one == 0) return 0;
return maxx * maxx;
}
/*2.累计和数组,建立好累加和数组后,遍历二维数组的每个位置,
对于任意(i,j),从该位置往(0,0)遍历所有正方形,正方形个数为min(i,j)+1
由于有了累加和数组,可以快速得到所有子正方形的和,比较和与边长平方是否相等,
相等则说明正方形中的数字都是1,更新maxx
Runtime: 64 ms, faster than 6.30% of C++ online submissions for Maximal Square.
Memory Usage: 10.5 MB, less than 92.59% of C++ online submissions for Maximal Square.*/
int maximalSquare2(vector>& matrix) {
if (matrix.size() == 0 || matrix[0].size() == 0) return 0;
vector > sum(matrix.size(), vector(matrix[0].size()));
int maxx = 0;
for (int i = 0; i < matrix.size(); i++) {
for (int j = 0; j < matrix[0].size(); j++) {
if (matrix[i][j] == '1') maxx = 1;
if (i == 0 && j == 0) sum[i][j] = matrix[i][j] - '0';
else if (i == 0) sum[i][j] = sum[i][j - 1] + (matrix[i][j] - '0');
else if (j == 0) sum[i][j] = sum[i - 1][j] + (matrix[i][j] - '0');
else sum[i][j] = sum[i][j - 1] + sum[i - 1][j] - sum[i - 1][j - 1]+(matrix[i][j]-'0');
}
}
for (int i = 1; i < matrix.size(); i++) {
for (int j = 1; j < matrix[0].size(); j++) {
if (matrix[i][j] == '1') {
int num = min(i, j)+1 ;//正方形个数
for (int k = 1; k <= num; k++) {
if (i - k < 0 && j - k >= 0 && sum[i][j] - sum[i][j - k] == k * k) maxx = max(maxx, k);
else if (i - k >= 0 && j - k < 0 && sum[i][j] - sum[i - k][j] == k * k) maxx = max(maxx, k);
else if (i-k>=0 && j-k>=0 && sum[i][j] - sum[i - k][j] - sum[i][j - k] + sum[i - k][j - k] == k * k) {
//说明是一个正方形
maxx = max(maxx, k);
}
else if (i - k < 0 && j - k < 0 && sum[i][j] == k * k) maxx = max(maxx, k);
}
}
}
}
return maxx * maxx;
}
int main() {
vector > matrix = { {'1','1'},{'1','1'}};
int res=maximalSquare2(matrix);
cout << res << endl;
return 0;
} 84. Largest Rectangle in Histogram
Hard
287770Add to ListShare
Given n non-negative integers representing the histogram's bar height where the width of each bar is 1, find the area of largest rectangle in the histogram.
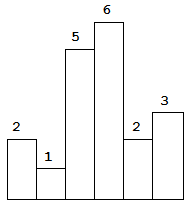
Above is a histogram where width of each bar is 1, given height = [2,1,5,6,2,3].
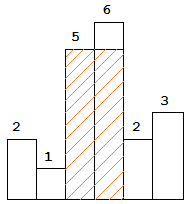
The largest rectangle is shown in the shaded area, which has area = 10 unit.
Example:
Input: [2,1,5,6,2,3] Output: 10
#include"pch.h"
#include
#include
#include
#include
using namespace std;
/*84. Largest Rectangle in Histogram
1.dp[i][j]存储从i到j最小数值,内存不够了*/
int largestRectangleArea1(vector& heights) {
if (heights.size() == 0) return 0;
vector > dp(heights.size(), vector(heights.size()));
int max = 0;
for (int i = 0; i < heights.size(); i++) {
dp[i][i] = heights[i];
if (max < dp[i][i]) max = dp[i][i];
}
for (int i = 0; i < heights.size(); i++) {
for (int j = i + 1; j < heights.size(); j++) {
if (heights[j] < dp[i][j - 1]) dp[i][j] = heights[j];
else dp[i][j] = dp[i][j - 1];
if (max < dp[i][j] * (j - i + 1)) max = dp[i][j] * (j - i + 1);
}
}
return max;
}
/*2.遍历数组,每找到一个数字大于后面的数字(局部峰值),
就向前遍历所有值,算出共同矩形面积。
为何从局部峰值处理:例如在[2,1,5,6,2,3]中,
局部峰值是2,6,3,非局部峰值的情况,局部峰值都可以包括,
例如1和5能组成的,到6都能组成,再加上6还能形成更大的。
Runtime: 12 ms, faster than 86.03% of C++ online submissions for Largest Rectangle in Histogram.
Memory Usage: 9.4 MB, less than 100.00% of C++ online submissions for Largest Rectangle in Histogram.*/
int largestRectangleArea2(vector& heights) {
int n = heights.size();
if (n == 0) return 0;
heights.push_back(0);
int maxx = 0;
for (int i = 0; i < n; i++) {
if (heights[i] > heights[i + 1]) {
int minn = heights[i];
maxx = max(maxx, minn);
for (int j = i-1; j >= 0; j--) {
minn = min(heights[j], minn);
maxx = max(maxx, minn*(i-j + 1));
}
}
}
return maxx;
}
/*3.维护一个栈,用来保存递增序列,相当于第二种方法中找局部峰值。
递增栈:维护递增顺序,遇到小于栈顶的就要处理
递减栈:维护递减顺序,遇到大于栈顶的开始处理
所以应当维护递增栈,当遇到小于栈顶的元素,就要开始计算举行面积了
由于栈顶是矩形高度,那么下面需要求宽度,所以单调栈中不能放高度,而是需要坐标,
从而可以直接计算出宽度
Runtime: 8 ms, faster than 98.53% of C++ online submissions for Largest Rectangle in Histogram.
Memory Usage: 9.6 MB, less than 100.00% of C++ online submissions for Largest Rectangle in Histogram.*/
int largestRectangleArea(vector& heights) {
heights.push_back(0);
int n = heights.size();
if (n == 1) return 0;
stack s;
int maxx = 0;
for (int i = 0; i < n; ++i) {
if (s.empty() || heights[i] > heights[s.top()]) s.push(i);
else {
int top = s.top();s.pop();
if (s.empty()) maxx = max(maxx, heights[top] * i);
else maxx = max(maxx, heights[top] * (i - s.top() - 1));
--i;
}
}
return maxx;
}
int main() {
vector nums = { 1,1 };
cout << largestRectangleArea(nums)<< endl;
return 0;
} 85. Maximal Rectangle
Hard
215357Add to ListShare
Given a 2D binary matrix filled with 0's and 1's, find the largest rectangle containing only 1's and return its area.
Example:
Input: [ ["1","0","1","0","0"], ["1","0","1","1","1"], ["1","1","1","1","1"], ["1","0","0","1","0"] ] Output: 6
#include"pch.h"
#include
#include
#include
#include
using namespace std;
/*85. Maximal Rectangle
每个层向上可以是一个直方图,计算每一层直方图的最大面积
Runtime: 44 ms, faster than 16.66% of C++ online submissions for Maximal Rectangle.
Memory Usage: 10.6 MB, less than 100.00% of C++ online submissions for Maximal Rectangle.*/
int maximalRectangle(vector>& matrix) {
if (matrix.size() == 0 || matrix[0].size() == 0) return 0;
int n = matrix.size(), m = matrix[0].size();
vector dp(m+1);//记录上一层的直方图数组
int res = 0;
for (int i = 0; i < n; i++) {
//对每一层构建例如84题的那种一位数组,从而构建每一层的直方图,求出每一层的最大面积
for (int j = 0; j < m; j++) {
if (matrix[i][j] == '0') dp[j] = 0;
else dp[j] += 1;
}
int maxx = 0;
stack s;
for (int j = 0; j <=m; j++) {
if (s.empty() || dp[j] > dp[s.top()]) s.push(j);
else {
int top = s.top(); s.pop();
if (s.empty()) maxx = max(maxx, dp[top] * j);
else maxx = max(maxx, dp[top] * (j - s.top() - 1));
j--;
}
}
res = max(maxx, res);
}
return res;
}
int main() {
vector > matrix = { {'1','0','1','0','0'},{'1','0','1','1','1'},
{'1', '1','1','1','1'} ,{'1','0','0','1','0'} };
int res = maximalRectangle(matrix);
cout << res;
return 0;
} 4. Median of Two Sorted Arrays
Hard
6037918Add to ListShare
There are two sorted arrays nums1 and nums2 of size m and n respectively.
Find the median of the two sorted arrays. The overall run time complexity should be O(log (m+n)).
You may assume nums1 and nums2 cannot be both empty.
Example 1:
nums1 = [1, 3] nums2 = [2] The median is 2.0
Example 2:
nums1 = [1, 2] nums2 = [3, 4] The median is (2 + 3)/2 = 2.5
#include"pch.h"
#include
#include
#include
#include
using namespace std;
/*4. Median of Two Sorted Arrays
两个有序数组的中位数,时间复杂度为 O(log (m+n)),二分法
如果有序数组长度是奇数,中位数就是中间那个,如果是偶数,就是中间两个数的平均值
设两个有序数组长度为n和m,长度之和为n+m,
分别找第 (m+n+1) / 2 个,和 (m+n+2) / 2 个,然后求其平均值即可,这对奇偶数均适用。
若 m+n 为奇数的话,那么其实 (m+n+1) / 2 和 (m+n+2) / 2 的值相等,
相当于两个相同的数字相加再除以2,还是其本身。
如何在两个有序数组中找到第K个元素:对K二分,分别在两个数组中找第K/2个元素,
需要检查一下,是否有第K/2个元素,如果有,就取出来,如果没有,就赋整型最大值,
比如 nums1 = {3},nums2 = {2, 4, 5, 6, 7},K=4,要找两个数组中的第4个数字,
首先先在nums1和nums2中找第2个数字,而nums1中只有1个数字,没有第2个数字,所以nums2中的前2个数字可以直接跳过,
因为要求在两个数组中找第4个数字,不管nums1中的数字有多大,第4个数字都不会在nums2的前两个数字中
Runtime: 20 ms, faster than 71.56% of C++ online submissions for Median of Two Sorted Arrays.
Memory Usage: 8.9 MB, less than 100.00% of C++ online submissions for Median of Two Sorted Arrays.
https://www.cnblogs.com/grandyang/p/4465932.html*/
int findKth(vector&nums1, int i, vector&nums2, int j, int K) {
if (i >= nums1.size()) return nums2[K + j - 1];
if (j >= nums2.size()) return nums1[K + i - 1];
if (K == 1) return min(nums1[i], nums2[j]);
int midVal1, midVal2;
if (i + K / 2 - 1 >= nums1.size()) midVal1 = INT_MAX;
else midVal1 = nums1[i + K / 2 - 1];
if (j + K / 2 - 1 >= nums2.size()) midVal2 = INT_MAX;
else midVal2 = nums2[j + K / 2 - 1];
if (midVal1 < midVal2) return findKth(nums1, i + K / 2, nums2, j, K - K / 2);
else return findKth(nums1, i, nums2, j + K / 2, K - K / 2);
}
double findMedianSortedArrays(vector& nums1, vector& nums2) {
int m = nums1.size(), n = nums2.size(), left = (m + n + 1) / 2, right = (m + n + 2) / 2;
return (findKth(nums1, 0, nums2, 0, left) + findKth(nums1, 0, nums2, 0, right)) / 2.0;
}
int main() {
vector nums1 = { 1,3 };
vector nums2 = { 2 };
cout << findMedianSortedArrays(nums1, nums2);
return 0;
} 295. Find Median from Data Stream
Hard
198338Add to ListShare
Median is the middle value in an ordered integer list. If the size of the list is even, there is no middle value. So the median is the mean of the two middle value.
For example,
[2,3,4], the median is 3
[2,3], the median is (2 + 3) / 2 = 2.5
Design a data structure that supports the following two operations:
- void addNum(int num) - Add a integer number from the data stream to the data structure.
- double findMedian() - Return the median of all elements so far.
Example:
addNum(1) addNum(2) findMedian() -> 1.5 addNum(3) findMedian() -> 2
Follow up:
- If all integer numbers from the stream are between 0 and 100, how would you optimize it?
- If 99% of all integer numbers from the stream are between 0 and 100, how would you optimize it?
class MedianFinder {
public:
/** initialize your data structure here.
数据流中的中位数,先使其有序,使用大小堆(都是大顶堆),大堆保存右半部分较大的数字,
小堆保存左半部分较小的数字,这样数组就被一分为二,当大、小堆元素数量相同时,
去首元素平均值,当小堆元素较多时,取小堆堆首。
从大堆和小堆取出的数字都是从大到小,因为都是默认的大顶堆,
每新来一个数字,先插入小堆,此时小堆堆首就是偏小的那半部分的数字中最大的,
将小堆堆首(存入相反数)插入大堆(这样,大堆存放的都是相反数,
大堆堆顶是相反数中最大的,就是原数字中最小的),并且将小堆堆首出堆,
此时,比较两个堆的大小,如果小堆size小于大堆,则将大堆中的最小的移动到小堆中。
使用priority_queue和multiset能实现相同功能。
Runtime: 184 ms, faster than 26.48% of C++ online submissions for Find Median from Data Stream.
Memory Usage: 41.8 MB, less than 100.00% of C++ online submissions for Find Median from Data Stream.*/
MedianFinder() {
}
void addNum(int num) {
small.push(num);
large.push(-small.top());
small.pop();
if(small.size()large.size()) return small.top();
else return 0.5*(small.top()-large.top());
}
private:
priority_queue small,large;
};
/**
* Your MedianFinder object will be instantiated and called as such:
* MedianFinder* obj = new MedianFinder();
* obj->addNum(num);
* double param_2 = obj->findMedian();
*/