SPSS(十二)SPSS对应分析(图文+数据集)
SPSS(十二)SPSS对应分析(图文+数据集)
对应分析的介绍
对应分析其实是对分类变量进行信息浓缩的方法,之前的主成分分析/因子分析针对的是连续型的变量
分析分类变量间关系时
- 卡方检验只能给出总体有无关联的结论,但不能进行精细分析,在变量类别极多时于事无补
- Logistic模型在多分类时我们可以使用哑变量,但是例如56各民族,我们要弄55个哑变量,自变量还要考虑交互项,几百个参数,过于笨拙
解决办法
- 精细建模:对数线性模型
对数线性模型在探究分类变量与分类变量之间的关系时非常强大,不过太过复杂,不好解释
- 直观展示:对应分析(对于对数线性模型我们可以偷点懒,不要那么精细,让其好解释一点)
对应分析的特点
- 是多维图示分析技术之一,结果直观、简单
- 与因子分析有关,等价于分类资料的典型相关分析
- 用于展示两个/多个分类变量各类间的关系(比如:高收入、黑人、男性倾向于反对开战)
- 研究较多分类变量间关系时较佳
- 各个变量的类别较多时较佳(均为四类以上)
对应分析的实质(理论很复杂,但是结果很明了简单)
- 就是对列联表中的数据信息进行浓缩,然后以易于阅读的图形方式呈现出来
- 以默认的卡方测量方式为例,首先以列联表为分析基础,计算基于H0假设的标化单元格残差
- 将每行看成是一条记录,基于列变量相关系数阵进行因子分析,计算出列变量各类的负荷值
- 将每列看成是一条记录,基于行变量相关系数阵进行因子分析,计算出行变量各类的负荷值
一句话来说就是计算出残差,残差做因子分析提取主成分之后绘图(散点图)表示
对应分析的局限性
- 不能进行变量间相关关系的检验,仍然只是一种统计描述方法
- 解决方案的所需维度需要研究者决定
- 对极端值敏感,对于小样本不推荐使用
案例:头发与颜色间存在何种关联
数据集如下
98 1 1
343 1 2
326 1 3
688 1 4
48 2 1
84 2 2
38 2 3
116 2 4
403 3 1
909 3 2
241 3 3
584 3 4
681 4 1
412 4 2
110 4 3
188 4 4
85 5 1
26 5 2
3 5 3
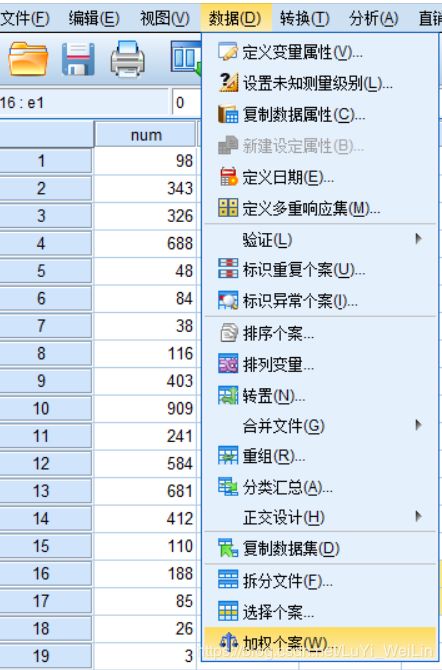
4 5 4第一列的数据是加权的
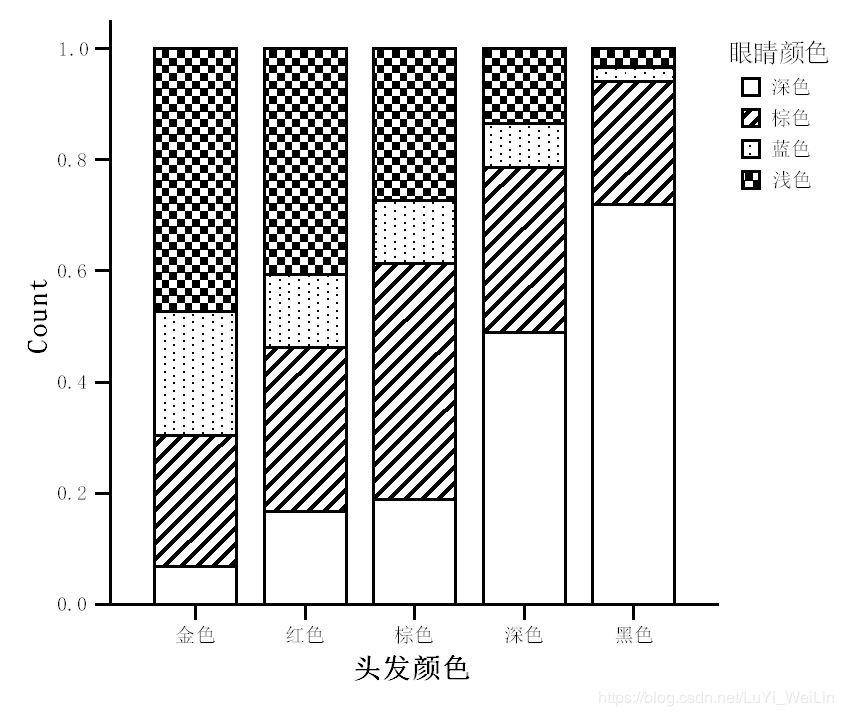
我们先使用百分比堆积图看会比较直观一些
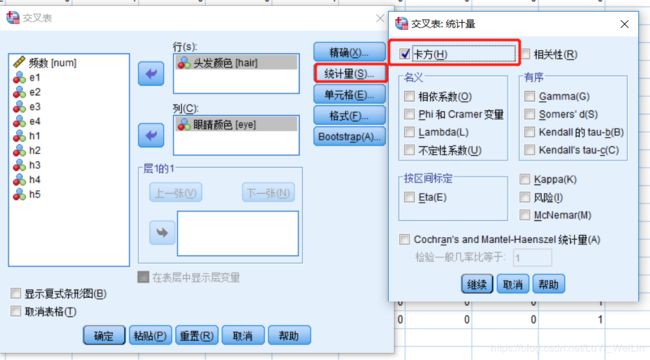
我们的对应分析就是比上面那个更加直观的表示出来,对应分析只是一种统计描述的方法,我们要先进行卡方检验
结果如下 :
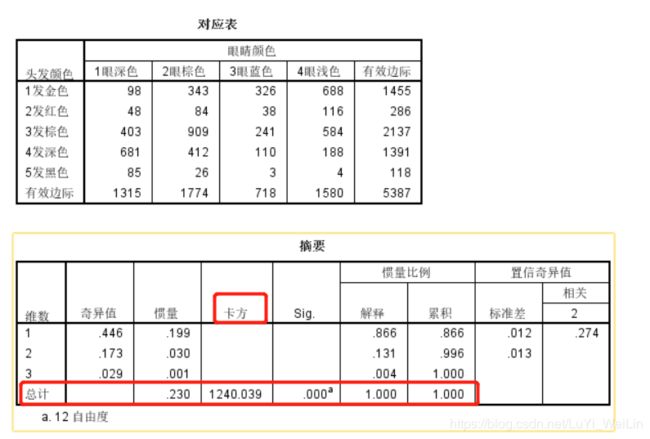
Pearson卡方检验Sig.<0.05证明两个变量并不是没有关联的,并不是完全独立的
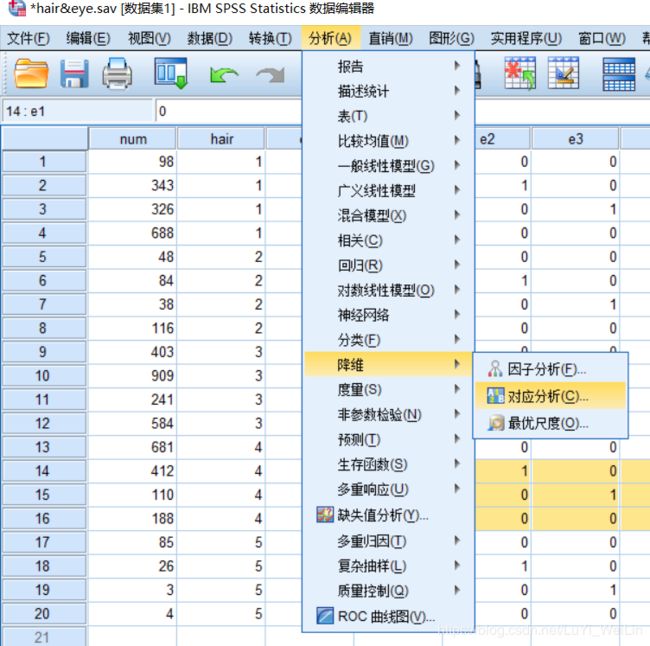
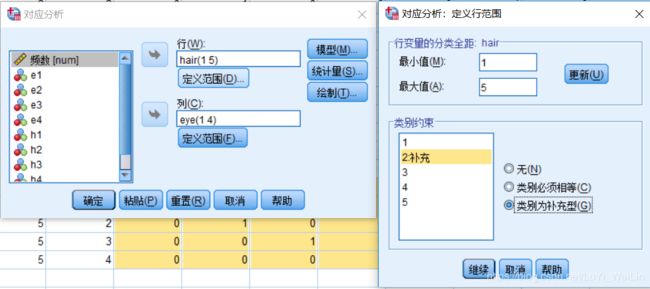
对应分析建模
定义其范围
结果解读
摘要:就是提取了几个维度,最多可以提取三个维度,我们看到其只取了两个维度;摘要里面有卡方检验,其实我们前面单独做卡方检验没有必要,和前面我们自己手动做卡方检验结果一致;比较有用的是惯量比例里面的解释,指的是这个信息携带了百分之多少的原始信息量
概述行、列点:在两个维度坐标空间中计算出其对应的坐标
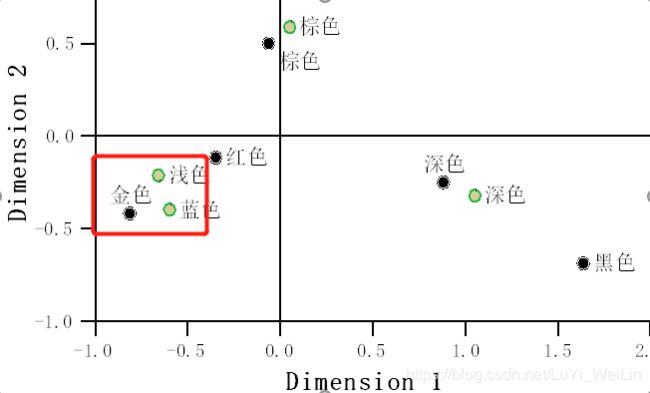
行和列点:这个就是对应分析图,也就是我们最终结果呈现
为了方便结果查看,我们添加X/Y参考线,位置都为0
(0,0)代表无任何倾向,无任何关联
得到这张图
对应分析图的阅读
每个维度可能代表了一种特征
实际上就是一个提取出的主成分,但由于分类变量的信息较少,可能找不到合理的解释
1.考察同一变量的区分度:如果同一变量不同类别在某个方向上靠得较近,则说明这些类别在该维度上区别不大。
2.考察不同变量的类别联系:一般而言,落在从图形原点(0,0)处出发相同方位上大致相同区域内的不同变量的分类点彼此有联系。散点间距离越近,说明关联倾向越明显;散点离原点越远,也说明关联倾向越明显。
(注意:远点周围的点不要去解释,因为原点代表无任何倾向,无任何关联)
对应分析图的正确解释:
- 错误的解释:金色头发的儿童中蓝色、浅色眼睛者居多
- 正确的解释:相对于平均水平而言,金色头发的儿童中蓝色、浅色眼睛的比例要高一些,也就是高于其他颜色头发的儿童
对应分析补充扩展
假如某一个变量的类别数据量太少我们不想纳入模型分析,可以设置其为补充型,选为补充型之后类别不会纳入模型,但是会显示结果
变量下面的框框,定义范围,类别约束里面选类别为补充型
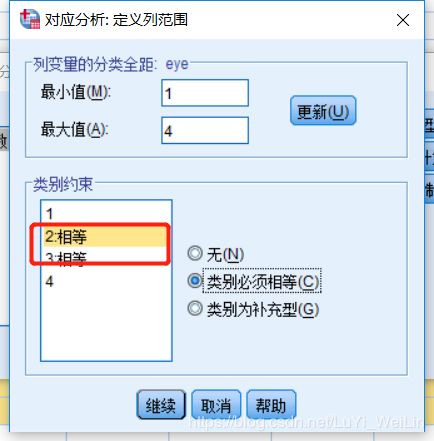
假如我们想把两个类别当成一个类别来观察,还是在刚才那里设置,设置为类别必须相等
对应分析中应注意的问题
分析目的:重在观察行、列变量间的联系
数据类型:无序分类较佳,如果均为有序分类,且变量较多时,采用多维偏好分析更合适
样本量:对极端值敏感,分析时有必要去除频数过少的单元格,对于小样本不推荐使用
变量间关联:不能将对应分析作为筛选相关变量的方法,变量纳入前最好先做卡方检验