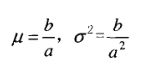13图像的复原

更多MATLAB图像处理视频请点击  http://study.163.com/course/courseMain.htm?courseId=1003594013 

由于拍摄技术或自然条件的限制，使的很多图像的质量降低，甚至有些图像十分模糊，掩盖了我们想得到的信息。图像的复原技术就是消除图像的模糊，产生一幅质量清晰的图像，例如对于运动模糊产生的图片，如果用肉眼直接观察很难对图像做出解释，这时需要利用图像复原技术来得到清晰的图像。

更多MATLAB图像处理视频请点击  http://study.163.com/course/courseMain.htm?courseId=1003594013

  本章主要描述如何利用MATLAB工具箱中的函数使图像变得更清晰，包括以下几部分：

   （1）图像的退化模型，对图像质量退化的原因和数学模型做 了简单的结束

    （2）图像的恢复模型，对图像反卷积的模型做了介绍

    （3）图像的复原方法，对MATLAB工具箱中提供的四种去模糊方法做了介绍

1 .图像的退化

    图像的退化是指在图像的获取传输过程中，由于成像系统、传输介质方面的原因，造成图像质量下降，典型的变现为图像模糊，、失真、含有噪声等。

   产生图像退化的原因有很多，常见的有以下几种：

  （1）目标或者拍摄装置的移动造成的运动模糊、长时间曝光引起的模糊等；

   （2）焦点没对准、光角引起的模糊、大气扰动引起的模糊、曝光时间太短引起拍摄装置捕获的光子太少引起的模糊等。

   （3）散焦引起的图像扭曲

     （4）图像在成像、数字化、采集和处理过程中引入噪声。

1.1 图像退化的属性模型

       图像复原的关键是建立图像的退化模型，一幅清晰的图像通过一个退化系统H,然后加入加性噪声能够生成一幅退化图像，图像的退化模型可用下图描述：

对图中所示的模型，可用数学表达式来表述：

  g（x，y）=h（x，y）*f（x，y）+n（x，y）

 其中，g（x，y）是指退化的图像，h（x，y）是指失真函数，f（x，y）为原图像，n（x，y）为加性噪声，*代表卷积运算

空间域的卷积运算对应于频域的相乘，所以上述公式可用频域模型表述为

 G（u，v）=H（u，v）F（u，v）+N（u，v）

其中，G（u，v），H（u，v），F（u，v），N（u，v）分别为g（x，y），h（x，y），f（x，y），n（x，y）的傅立叶变换

上面的退化模型可以简写为：

     g=Hf+n

 其中，g是指质量退化的图像， H是指失真函数，即点扩散函，点扩散函数描述的是一个光学系统对真实图像的模糊程度，f是指真实图像，n是指加性噪声。

 从模型中，我看可以看出，图像去模糊的主要任务是用点扩散函数反卷积模糊的图像。

例：对清晰的图像通过卷积一个特殊的点扩散函数来产生模糊的图像

I=imread('peppers.png');
figure,subplot(121),imshow(I),title('原图');
LEN=31;
THETA=11;
PSF=fspecial('motion',LEN,THETA);  %fspecial函数详解，百度词条

%http://baike.baidu.com/link?url=2lYu8whcELuqCIU35z_PMMSgR0LuQEYN7FO4fCPUpBUIjUUymYZxK-CY_PfB2-xmM1OQSY7j3mfIAy4PjTjwTy1z6wBqMe5B1xxpxT3WSY_

Blurred=imfilter(I,PSF,'circular','conv');
subplot(122),imshow(Blurred),title('模糊后的图');

1.2 图像的噪声

    数字图像的噪声主要来自数字图像的获取和传输过程。图像的噪声种类有很多，常见的噪声有高斯噪声，瑞利噪声，伽马噪声，指数分布噪声，均匀分布噪声，椒盐噪声等。

   （1）高斯噪声的概率密度函数为：

    

 （2）瑞利噪声的概率密度函数为：

（3）伽马噪声的概率密度函为：

 

其中，z表示像素值，a>0，b为正整数，其均值和方差由下式确定：

 

（4）指数分布噪声的概率密度函数为：

（5）均匀分布的噪声的概率密度函为：

（6）椒盐噪声的概率密度函数为：

MATLAB图像处理工具箱中的 imnoise函数可以在图像中加入噪声

&百度百科imnoise详解http://baike.baidu.com/link?url=OkVBVlgRxuuCuL8hzXhMwASsd5AhAgkuXa6cUoZ42522dtxYiEQUP0ZhAROPQExkui9Qj8KMhVagRDtyvo1ITfE80grVnvXfl_-VR7ASQNW

或者在MATLAB中 help imnoise

例：

I=imread('eight.tif');
J=imnoise(I,'salt & pepper',0.02);%加入椒盐噪声，噪声密度为0.02
>> subplot(121),imshow(I),title('原图');
>> subplot(122),imshow(J),title('加入椒盐噪声');

2. 图像复原的模型和方法分类

   图像的复原是图像退化的逆过程，它尽可能地恢复退化图像的本来面目，一般来说，图像复原是指在建立系统退化模型的基础上，以退化图像为依据，运用某些先验知识，将劣化了的图像以最大的保真度复原图像。

  可见，图像的复原关键取决于对于图像退化过程的先验知识所掌握的精度和建立的退化模型是否合适。

2.1 图像的复原模型可以用下图来描述

 

其中，g（x，y）是指退化的图像，w（x，y）是指图像复原滤波器，f（x，y）是指恢复的图像。

 广义上讲，图像复原是一个求逆问题，逆问题经常不存在唯一解， 不存在解，因此图像恢复一般比较困难。为了得到一个有用解，图像复原往往需要一个评价标准，即衡量其接近真实图像的程度，或者说对退化图像的估计是否是得到了某种准则下的最优。这需要有先验知识及对解的附加约束条件。

  由于引起图像质量退化的原因有很多，因此为了消除图像质量的退化而采取的图像复原方法有多种，而恢复的质量标准也不尽相同，因此图像的复原是一个复杂的数学工程，其方法技术也各不相同。

  在给定退化模型的情况下，图像复原可以分为无约束和有约束两大类；而根据是在频域恢复还是在空域恢复图像，图像复原可以划分为频域复原方法和空域复原方法。

 2.2 无约束复原方法

   由前面结束的模型可以知道，噪声可以表示为

      n=g-Hf

    在不知道噪声的情况下，我们希望噪声项尽可能的小，也就是希望找到一个f，希望Hf在最小二乘方情况下近似g，也就是说，希望找到一个图像复原滤波器f，使得

            ||n||^2=||g-Hf||^2

      最小。因此上述问题就可以转化为一个无约束的优化问题，即：

         min||g-Hf||^2

    应用求无约束优化问题的方法，可以求得这种情况下的解为：
   

2.3 有约束复原方法

   在无约束复原方法的基础上，为了使用更多的先验信息，常常附加约束条件来提供图像的复原精度，例如可以令L为f的线性算子，那么最小二乘法复原问题就可以转化为使形式为||Lf||^2的函数服从约束条件||g-Hf||^2=||n||^2的最小问题。这个最小值问题可以使用拉格朗日来求解。

  

2.4 复原方法的评估

 在使用各种图像复原方法得到复原的图像后，需要评估一下各种方法的优劣，一般在计算机模拟中，使用信噪比的改善来评价复原质量的好坏。

 计算信噪比的改善的公式为：

3 图像的复原方法

 MATLAB的图像处理工具箱中提供了四种图像复原的函数，分别利用维纳滤波器（wiener）复原，规则化滤波器（regularized）复原，Lucy-Richardson方法复原和盲反卷积复原。

 图像复原的四种函数

 函数名              滤波器

deconvwnr     用wiener滤波器实现图像去模糊

deconvreg     用regularized滤波器实现图像去模糊

deconvlucy    用Lucy-Richardson滤波器实现图像去模糊

deconvbind    用盲反卷积算法实现图像去模糊

其中

deconvwnr函数求得的是最小二乘解

deconvreg 函数求得的是一种约束最下二乘解，在使用此函数时若提供一些关于噪声的参数可以减少去模糊过程中噪声的放大作用。

deconvlucy 函数使用的是一种快速抑制的Lucy-Richardson方法， 经过多次迭代，采用优化技术和泊松统计准则，不需要函数提供模糊图像中关于噪声的额外参数。

使用deconvbind函数时不需要知道真实的点扩散函PSF，使用盲反卷积技术，只需要初始设置一个PSF参数，函数除了返回恢复出的图像外，还返回最后跌倒的点扩散函数PSF。

3.1 维纳滤波

在知道清晰图像和噪声频率特性的情况下，维纳滤波器被看作是一种有效的图像复原技术，如果没有加性噪声，维纳滤波器方法就退化为倒滤波方法。维纳滤波器的频域形式为：

在MATLAB图像处理工具箱中，使用deconvwnr函数来进行维纳滤波器图像复原，deconvwnr函数的常见调用方法如下：

J=deconvwnr（I，PSF）

J=deconvwnr（I，PSF，NSR）

J=deconvwnr（I，PSF，NCORR，ICORR）

其中

I值退化的图像，是原图像卷积一个点扩散函数PSF然后加上加性噪声而得到的。

NSR 是噪声信号功率比，可以为一标量，也可以为与I同样大小的矩阵，默认值为0.

NCORR和ICORR分别是信号和原图像的自相关函数

J是返回的复原图像。

例：通过一个例子来看一下维纳滤波器的效果

I=checkerboard(8);%checkboard(n)函数：创建一个黑白或者说棋盘格图像nxn。
noise=0.1*randn(size(I));%自定义的噪声
PSF=fspecial('motion',21,11);%产生运动模糊的滤波器
Blurred=imfilter(I,PSF,'circular');%产生运动模糊的图像
BlurredNoisy=im2uint8(Blurred+noise);%运动模糊的图像加上噪声
NSR=sum(noise(:).^2)/sum(I(:).^2);%噪声信号功率比

NP=abs(fftn(noise)).^2;
NCORR=fftshift(real(ifftn(NP)));%噪声自相关函数
% 根据傅立叶变换与卷积的关系得到的。
%同理，求出原图像的自相关函数
IP=abs(fftn(I)).^2;
ICORR=fftshift(real(ifftn(IP)));

%依次改变各个参数进维纳滤波
J1=deconvwnr(BlurredNoisy,PSF);
J2=deconvwnr(BlurredNoisy,PSF,NSR);
J3=deconvwnr(BlurredNoisy,PSF,NCORR,ICORR);
figure;%显示原图像，退化的图像和维纳滤波后的图像
subplot(321),imshow(I),title('原图像');
subplot(322),imshow(BlurredNoisy),title('退化的图像');
subplot(323),imshow(J1),title('deconvwnr(BlurredNoisy,PSF)');
subplot(324),imshow(J2),title('deconvwnr(BlurredNoisy,PSF,NSR)');
subplot(325),imshow(J3),title('deconvwnr(BlurredNosiy,PSF,NCORR,ICORR)');

通过程序的运行结果，可以看到，对于维纳滤波器，分别使用不同的参数，会得到不同的复原图像。

3.2规则化滤波

规则化滤波器是在知道噪声信息的情况下有效的饭卷积方法，在MATLAB中进行规则化滤波器的函数是deconvreg。deconvreg的调用方法如下：

J=deconvreg(I,PSF);

J=deconvreg(I,PSF,NOISEPOWER)

J=deconvreg(I,PSF,NOISERPOWER,LRANGE);

J=deconvreg(I,PSF,NOISERPOWER,LRANGE,REGOP)

[J,LAGRA]=deconvreg(I,PSF,NOISEPOWER,LRANGE,REGOP)

其中：

I是指退化的图像

PSF是指点扩散函数

NOISEPOWER是加性噪声的能量，默认值为0；

LRANGE是函数优化过程中拉格朗日算子的范围，默认值为[1e-9,1e9]

REGOP是约束优化中的规则化操作，默认值为Laplacian

J是去模糊后返回的图像

LAGRA是返回的拉格朗日算子

例：规则化图像复原

 I=checkerboard(8);%产生一个8*8跳棋盘图像
PSF=fspecial('gaussian',7,10);%产生一个高斯低通滤波器，模板尺寸为[7 7],滤波器的标准差为10
V=0.01;%高斯加性噪声的标准差
IF1=imfilter(I,PSF);%高斯低通滤波
BlurredNoisy=imnoise(IF1,'gaussian',0,V);%原图像通过高斯低通滤波器后，加入高斯噪声
NOISEPOWER=V*prod(size(I));%计算噪声的能量
[J LAGRA]=deconvreg(BlurredNoisy,PSF,NOISEPOWER);%反卷积，返回复原后的图像和拉格朗日乘子
subplot(321),imshow(I),title('原图像');
>> subplot(322),imshow(BlurredNoisy),title('退化后的图像');%显示退化后的图像
>> subplot(323),imshow(J),title('J LAGRA]=deconvreg(BlurredNoisy,PSF,NP)');%显示复原后的图像
>> J1=deconvreg(BlurredNoisy,PSF,[],LAGRA/10);%改变函数中的参数
>> subplot(324),imshow(J1),title('deconvreg(BlurredNoisy,PSF,[],LAGRA/10)');%显示复原后的图像
>> J2=deconvreg(BlurredNoisy,PSF,[],LAGRA*10);%改变函数中的参数
>> subplot(325),imshow(J2),title('deconvreg(BlurredNoisy,PSF,[],LAGRA*10)');

对于规则化滤波，改变deconvreg函数中的参数，会得到不同的复原图像

3.3 Lucy-Richardson滤波

 Lucy-Richardson滤波器方法假设噪声服从泊松分布，基于贝叶斯理论使产生图像的似然性达到最大值。在MATLAB图像处理工具箱中，使用使用Lucy-Richardson滤波器方法复原图像的函数为deconvlucy，该函数在最初的Lucy-Richardsom方法的基础上进行了一下改进：

减少方法噪声的影响

对图像质量不均匀的像素进行修正

这些改进加快了图像复原的速度和复原的效果。在前面介绍的方法中，噪声放大是一个严重的问题，尤其对于光滑的图像来说，一些斑点会使图像的质量很差，为了抑制噪声放大，deconvlucy函数使用了衰减因子dampar，这个参数限制了恢复的图像跟原始图像之间的差异，小于这个参数衰减进行，大于这个参数迭代就被抑制。

deconvlucy函数的使用方法如下：

J=deconvlucy（I，PSF）；

J=deconvlucy（I，PSF，NUMIT）

J=deconvlucy（I，PSF，NUMIT，DAMPAR）

J=deconvlucy（I，PSF，NUMIT，DAMPAR，WEIGHT）

J=deconvlucy（I，PSF，NUMIT，DAMPAR，WEIGHT，READOUT）

J=deconvlucy（I，PSF，NUMIT，DAMPAR，WEIGHT，READOUT，SUBSMPL）

其中：

I是指要复原的退化图像

PSF是点扩散函数

NUMIT是指迭代的次数，默认值为10；

DAMPAR规定了原图像和恢复图像之间的偏差

WEIGHT是一个权重矩阵，它规定了图像I中的坏像素的权值为0，其他的为1，默认值为跟I同样维度的全1矩阵

READOUT是与噪声和读出设备有关的参数，默认值为0

SUBSMPL是指二次抽样频率，默认值为1；

J是反卷积后输出的图像

PSF是最后反卷积后得到的点扩散函数

例：Lucy-Richardson方法复原图像

=checkerboard(8);%产生一个8x8的跳棋盘图像
>> PSF=fspecial('gaussian',7,10);%产生一个高斯低通滤波器，模板尺寸为[7 7],滤波器的标准差为10
>> V=0.0001;%高斯加性噪声的标准差
>> IF1=imfilter(I,PSF);%原图像通过高斯低通滤波器
>> BlurredNoisy=imnoise(IF1,'gaussian',0,V);%加入高斯噪声
>> WT=zeros(size(I));%产生权重矩阵
>> WT(5:end-1,5:end-4)=1;
>>
>> %使用不同的参数进行复原
>> J1=deconvlucy(BlurredNoisy,PSF);
>> J2=deconvlucy(BlurredNoisy,PSF,20,sqrt(V));
>> J3=deconvlucy(BlurredNoisy,PSF,20,sqrt(V),WT);
>> figure;%依次显示原图像，模糊后的图像和deconvlucy方法得到的图像
>> subplot(321),imshow(I),title('原图像');
>> subplot(322),imshow(BlurredNoisy),title('模糊后的图像');
>> subplot(323),imshow(J1),title('deconvlucy(A,PSF)');
>> subplot(324),imshow(J2),title('deconvlucy(A,PSF,NI,DP)');
>> subplot(325),imshow(J3),title('deconvlucy(A,PSF,NI,DP,WT)');

对于Luch-Richardson方法滤波，改名deconvlucy函数中的参数，会得到不同的复原图像。

3.4 盲反卷积

  盲反卷积方法是在Lucy-Richardson算法的基础上改进的方法，该方法在不知道模糊和噪声信息的情况下有效，在MATLAB图像处理工具箱中，使用盲反卷积进行图像复原的函数为deconvblind，调用格式如下：

  [J,PSF]=deconvblind(I,INITPSF);

  [J,PSF]=deconvblind(I,INITPSF,NUMIT)

  [J,PSF]=deconvblind(I,INITPSF,NUMIT,DAMPAR)

  [J,PSF]=deconvblind(I,INITPSF,NUMIT,DAMPAR,WEIGHT)

  [J,PSF]=deconvblind(I,INITPSF,NUMIT,DAMPAR,WEIGHT,READOUT)

其中：

 I是指要恢复的模糊图像。

INITPSF是初始的PSF函数

NUMIT是指迭代的次数，默认值为10；

 DAMPAR规定了原图像和恢复图像之间的偏差

 WEIGHT是一个权重矩阵，它规定了图像I中的坏像素的权值为0，其他的为1，默认值为跟I同样维数的全1矩阵

 READOUT是与噪声和读出设备有关的参数，默认值为0

 J是反卷积恢复出来的图像

 PSF是最后反卷积后得到的点扩散函数

例：盲反卷积恢复图像

I=checkerboard(8);%产生一个8*8的跳棋盘图像
>> PSF=fspecial('gaussian',7,10);%产生一个高斯低通滤波器，模板尺寸为[7 7],滤波器的标准差为10
>> V=0.0001;%高斯加性噪声的标准差
>> IF1=imfilter(I,PSF);%原图像通过高斯低通滤波器
>> BlurredNoisy=imnoise(IF1,'gaussian',0,V);%加入高斯噪声:
>> WT=zeros(size(I));%产生权重矩阵
>> WT(5:end-4,5:end-4)=1;
>> INITPSF=ones(size(PSF));%初始化最初的点扩散函数
>> [J P]=deconvblind(BlurredNoisy,INITPSF,20,10*sqrt(V),WT);
>> figure;%依次显示原图像，模糊图像，真实的PSF，盲反卷积得到的图像和恢复的PSF
>> subplot(321),imshow(I),title('原图像');
>> subplot(322),imshow(BlurredNoisy),title('模糊图像');
>> subplot(323),imshow(PSF,[]),title('真实的PSF');
>> subplot(324),imshow(J),title('复原的图像');
>> subplot(325),imshow(P,[]),title('复原的PSF');

更多MATLAB图像处理视频请点击  http://study.163.com/course/courseMain.htm?courseId=1003594013