数据结构——树学习总结（一）

一、二叉树

二叉树是一种特殊的树。二叉树的特点是每个结点最多有两个儿子。 
二叉树使用范围最广。一颗多叉树也可以转化为二叉树。 

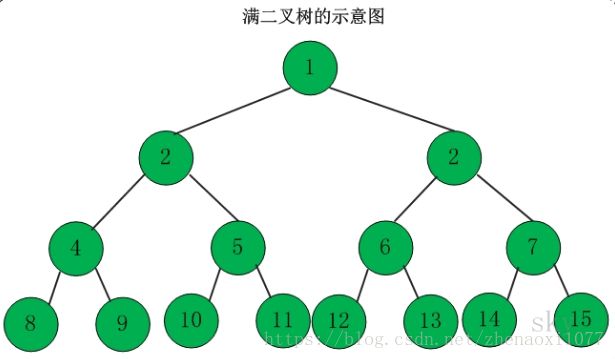
1、满二叉树

          二叉树中每个内部节点都有两个儿子。满二叉树所有的叶节点都有相同的深度。 
          满二叉树是一棵深度为h且有个结点的二叉树。 

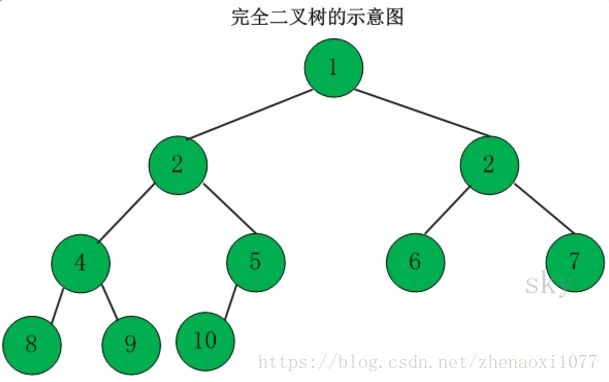
2、完全二叉树

       若设二叉树的高度为h，除了第h层外，其他层的结点数都达到最大个数，第h层从右向左连续 缺若干个结点，则为完全二叉树。 

特点： 
由上图发现：

1）如果一棵完全二叉树的父节点编号为,则其左儿子的编号是,右儿子的结点编号为, 
2）已知完全二叉树的总节点数为n求叶子节点个数： 
当n为奇数时：（n+1）/2 
当n为偶数时 : （n）/2

3）已知完全二叉树的总节点数为n求父节点个数：为：n/2

4）已知完全二叉树的总节点数为n求叶子节点为2的父节点个数： 
当n为奇数时：n/2 
当n为偶数时 : n/2-1

5）如果一棵完全二叉树有N个结点，那么这棵二叉树的深度为（向上取整） 
      完全二叉树最典型的应用就是堆。

3、遍历 

二叉树的遍历(要有递归的思想！！！)：（代码在后边）

1：先序遍历：根->左子树->右子树（先序）（如果用非递归，就是使用栈）

2：中序遍历：左子树->根->右子树（中序）

3：后序遍历：左子树->右子树->根（后序）

这三种遍历方法只是访问结点的时机不同，访问结点的路径都是一样的，时间和空间复杂度皆为O(n)。

4、二叉树的存储结构

（1）顺序存储（只适用于完全二叉树）——可以用于排序算法中的堆排序

（2）链式存储（最普遍的存储方式）——由于结点可能为空，所以会比较浪费空间

         如果有n个节点，则有2n个left、right指针，但是用到的只有n-1个指针

（3）线索存储（改进的方法）

 二、二分搜索树

1、定义

（1）特征

• 二分搜索树本质上是一棵二叉树。
• 每个节点的键值大于左孩子
• 每个节点的键值小于右孩子
• 以左右孩子为根的子树仍为二分搜索树

    注意：上篇博文中讲解的堆是一棵完全的二叉树，但对于二分搜索而言，并无此限制，例如下图。

2、优势

（1）查找表的实现 - 字典数据结构

       查找表的实现，通常这种实现又被称为“字典数据结构”，都是以键值对形式形成了表，通过key来查找对应value。如果这些key值都是整型，那么可以使用数组实现，但是在实际运用中key值是比较复杂的，例如字典。因此需要实现一个“查找表”，最基础方式就是二分搜索树。

（2）时间复杂度比较

       通过以上分析，其实普通数组和顺序数组也可以完成以上需求，但是操作起来消耗的时间却不尽人意。

（3）高效性

       不仅可查找数据，还可以高效地插入，删除数据之类的动态维护数据。
可以方便地回答很多数据之间的关系问题： 

• min, max
• floor, ceil
• rank
• select
   

 3、代码实现

在代码实现堆时，正是因为它是一棵完全的二叉树此特点，所以可使用数组进行实现，但是二分搜索树并无此特性，所以在实现上是设立key、value这种Node节点，节点之间的连续使用指针。

Node节点结构体包含：

Key key;
Value value;
Node *left; //左孩子节点指针
Node *right; //右孩子节点指针

私有成员变量：

Node *root; // 根节点
int count; // 节点个数

公有基本方法：

BST() // 构造函数, 默认构造一棵空二分搜索树
int size() // 返回二分搜索树的节点个数
bool isEmpty() // 返回二分搜索树是否为空

// 二分搜索树
template 
class BST{

private:
    // 二分搜索树中的节点为私有的结构体, 外界不需要了解二分搜索树节点的具体实现
    struct Node{
        Key key;
        Value value;
        Node *left;
        Node *right;

        Node(Key key, Value value){
            this->key = key;
            this->value = value;
            this->left = this->right = NULL;
        }
    };

    Node *root; // 根节点
    int count;  // 节点个数

public:
    // 构造函数, 默认构造一棵空二分搜索树
    BST(){
        root = NULL;
        count = 0;
    }
    ~BST(){
        // TODO: ~BST()
    }

    // 返回二分搜索树的节点个数
    int size(){
        return count;
    }

    // 返回二分搜索树是否为空
    bool isEmpty(){
        return count == 0;
    }
};

（1）插入新节点

       查看以下动画演示了解插入新节点的算法思想：（其插入过程充分利用了二分搜索树的特性）。例如待插入数据60，首先与根元素41比较，大于根元素，则与其右孩子再进行比较，大于58由于58无右孩子，则60为58的右孩子，过程结束。（注意其递归过程）

       代码实现：insert函数。判断node节点是否为空，为空则创建节点并将其返回（ 判断递归到底的情况）。
若不为空，则继续判断根元素的key值是否等于根元素的key值： 

• 若相等则直接更新value值即可。
• 若不相等，则根据其大小比较在左孩子或右孩子部分继续递归直至找到合适位置为止。

//insert 递归版
void *insert(Key key, Value value)
{
    root = __insert(root, key, value);
}

//向以 node 为根节点的树中插入元素
Node *__insert(Node *node, Key key, Value value)
{
    if (node == NULL)
    {
        count++;
        return new Node(key, value);
    }


    if (node->key == key)
    {
        node->value = value;
    }

    if (node->key > key)
        node->right = insert(node->right, key, value);
    else
        node->left = insert(node->left, key, value);

    return node;
}


//insert 非递归版
void *insert(Key key, Value value)
{
    Node *pre = root;
    Node *p = root;
    if (p == NULL)
    {
        count++;
        root = new Node(key, value);
        return;
    }

    while (p)
    {
        if (p->key == key)
        {
            p->value = value;
            return;
        }

        if (p->key < key)
        {
            pre = p;
            p = p->right;
        }
        else
        {
            pre = p;
            p = pre->left;
        }
    }

    if (pre->left == p)
        pre->left = new Node(key, value);
    else
        pre->right = new Node(key, value);

}

 （2）查找
      其实在理解二分搜索树的插入过程后，其查找过程本质上是相同的，这里提供两个搭配使用的查找函数：

• bool contain(Key key)：查看二分搜索树中是否存在键key
• Value* search(Key key)：在二分搜索树中搜索键key所对应的值。如果这个值不存在, 则返回NULL。（注意：这里返回值使用Value* ，就是为了避免用户查找的值并不存在而出现异常）

public:
   // 查看二分搜索树中是否存在键key
    bool contain(Key key){
        return contain(root, key);
    }

    // 在二分搜索树中搜索键key所对应的值。如果这个值不存在, 则返回NULL
    Value* search(Key key){
        return search( root , key );
    }

private:
    // 查看以node为根的二分搜索树中是否包含键值为key的节点, 使用递归算法
    bool contain(Node* node, Key key){

        if( node == NULL )
            return false;

        if( key == node->key )
            return true;
        else if( key < node->key )
            return contain( node->left , key );
        else // key > node->key
            return contain( node->right , key );
    }

    // 在以node为根的二分搜索树中查找key所对应的value, 递归算法
    // 若value不存在, 则返回NULL
    Value* search(Node* node, Key key){

        if( node == NULL )
            return NULL;

        if( key == node->key )
            return &(node->value);
        else if( key < node->key )
            return search( node->left , key );
        else // key > node->key
            return search( node->right, key );
    }
};

 （3）遍历（深度，层次）

        遍历前面讲啦，前序/中序/后序都是深度优先遍历，层次遍历是广度优先遍历。

//前序遍历
void preOrder()
{
    __preOrder(root);
}

void __preOrder(Node *node)
{
    if (node != NULL)
    {
        cout << node->value << endl;
        __preOrder(node->left);
        __preOrder(node->right);
    }
}

//中序遍历
void inOreder()
{
    __inOrder(root);
}

void __inOrder(Node *node)
{
    if (node != NULL)
    {
        __inOrder(node->left);
        cout << node->value << endl;
        __inOrder(node->right);
    }
}

//后序遍历
void postOreder()
{
    __postOrder(root);
}

void __postOrder(Node *node)
{
    if (node != NULL)
    {
        __postOrder(node->left);
        __postOrder(node->right);
        cout << node->value << endl;
    }
}


//层次遍历
void levelOrder()
{
    queue q;
    q.push(root);

    while (!q.empty())
    {
        Node *node = q.front();
        q.pop();
        count--;

        cout << node->key << endl;
        if (node->left)
            q.push(node->left);
        if (node->right)
            q.push(node->right);
    }   
}

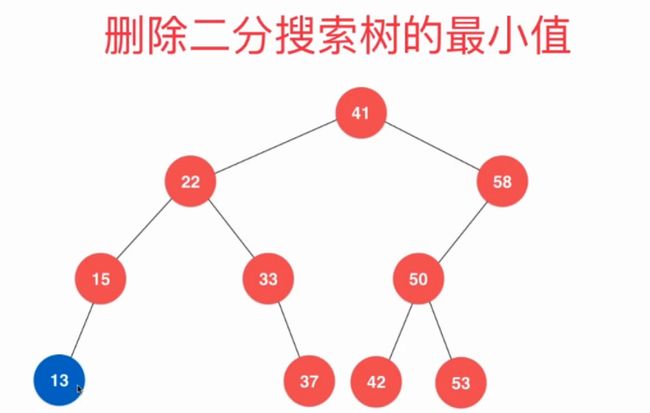
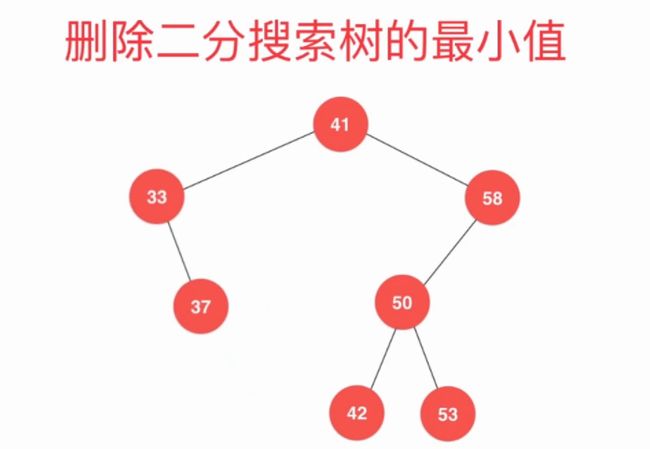
（4）删除最小/大值

         都是这个理儿，只演示最小值。这个要分情况：

             1）直接删除

 

             2）调整删除

void removeMin()
{
    if (root)
    {
        root = __removeMin(root);
    }
}

//删除 以node为根的树的最小值
Node *__removeMin(Node *node)
{
    if (node->left == NULL)
    {
        Node *rightNode = node->right;          //当前要删节点的右孩子
        delete node;
        count--;
        return rightNode;
    }

    node->left =  __removeMin(node->left);
    return node;
}

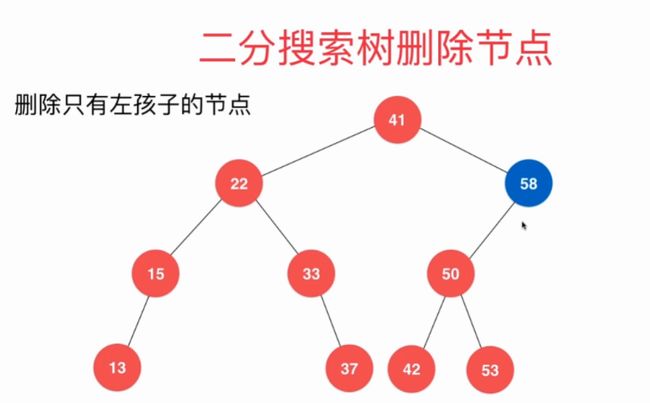
（5）删除任意节点

 

//删除 任意节点
void remove(Key key)
{
    root = __remove(root, key);
}

Node *__remove(Node *node,Key key)
{
    if (node == NULL)
    {
        return NULL;
    }

    if (node->key > key)
    {
        node->left = __remove(node->left, key);
        return node;
    }
    else if (node->key < key)
    {
        node->right = __remove(node->right, key);
        return node;
    }
    else
    {
        if (node->left == NULL)         //与删除最小值类似
        {
            Node *rightNode = node->right;
            delete node;
            count--;
            return rightNode;
        }
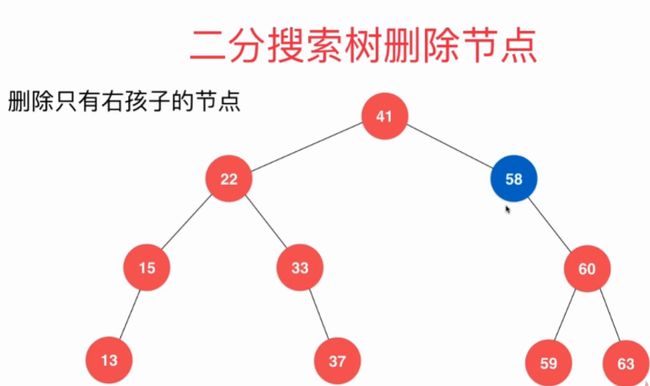
        else if (node->right == NULL)   //与删除最大值类似
        {
            Node *leftNode = node->left;
            delete node;
            count--;
            return leftNode;
        }
        else            //node->left!=NULL && node->right!=NULL
        {
            //找到右子树中的最小值，即为即将代替要删节点
            /*Node *successor = __minimum(node->right);
            successor->right = __removeMin(node->right);*/

            //上式__removeMin（）会将successor删除，致使successor变为空指针
            //解决：将右子树中的最小值复制一份，另写一个Node构造函数
            Node *successor = new Node(__minimum(node->right));
            count++;
            successor->right = __removeMin(node->right);
            successor->left = node->left;

            delete node;
            count--;

            return successor;
        }
        
    }
}

（6）链表与二分搜索树 查找时间复杂度比较
        将《圣经》中的内容存放在txt文件中，分别用以上实现的二分搜索树BST、顺序查找表SST（本质是一个链表）来统计文件中“god”的词频时间复杂度。（注: 这个词频统计法相对简陋, 没有考虑很多文本处理中的特殊问题，在这里只做性能测试，具体的测试代码在github源码中查看）

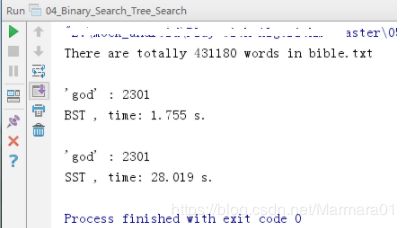
       结果展示：

       结论分析：以上的结果已经显而易见，“god”一词在《圣经》中出现了2301此，但是二分搜索树只需1.7秒就获取了结果，而链表却消耗了28秒，本质上的差别显而易见，体现出了二分搜索树的高效性。