数据库第六章总结+课后题（2020.4.13作业）

两个小节，问题的提出和规范化。
主要是规范化，定义比较多

问题的提出

规范化

函数依赖

函数依赖：设R(U)是一个属性集U上的关系模式，X和Y是U的子集。若对于R(U)的任意一个可能的关系r，r 中不可能存在：两个元组在X上的属性值相等，而在Y上的属性值不等， 则称“X函数确定Y”或“Y函数依赖于X”，记作X→Y。

平凡与非平凡：X→Y，但Y⊈X则称X→Y是非平凡的函数依赖。X→Y，但Y⊆X 则称X→Y是平凡的函数依赖。
若X→Y，则X称为这个函数依赖的决定因素
若X→Y，Y→X，则记作X←→Y。
若Y不函数依赖于X，则记作X$\nrightarrow$Y。

完全函数依赖与部分函数依赖：在R(U)中，如果X→Y，并且对于X的任何一个真子集X’, 都有 X’$\nrightarrow$Y, 则称Y对X完全函数依赖，记作X → Y。若X→Y，但Y不完全函数依赖于X，则称Y对X部分函数依赖，记作X → Y。

传递函数依赖：在R(U)中，如果X→Y(Y⊈X)，Y$\nrightarrow$X，Y→Z，Z⊈Y, 则称Z对X传递函数依赖(transitive functional dependency)。记为：X → Z。
注: 如果Y→X, 即X←→Y，则Z直接依赖于X，而不是传递函数依赖。

码

设K为R中的属性或属性组合。若K → U，则K称为R的一个候选码(Candidate Key)。

如果U部分函数依赖于K，即K → U,则K称为超码 。
候选码是最小的超码，即K的任意真子集都不是候选码。

若关系模式R有多个候选码，则选定其中的一个做为主码(Primary key)。

主属性与非主属性：包含在任何一个候选码中的属性 ，称为主属性。不包含在任何码中的属性称为非主属性
整个属性组是码，称为全码（All-key）

关系模式R中属性或属性组X并非R的码，但X是另一个关系模式的码，则称X是R的外部码（Foreign key）也称外码。

范式（重点）

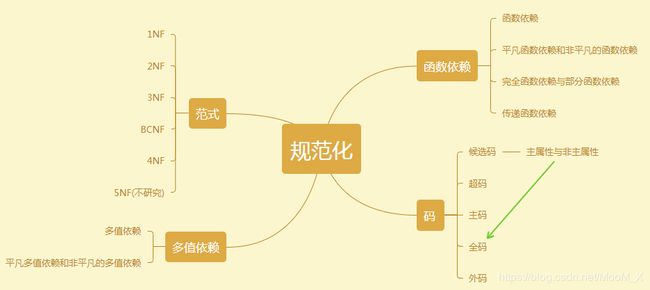
分为六种，联系如下，研究前五种

第一范式1NF
二维表每个分量必须是不可分开的数据项。满足了这个条件的关系模式就属于第一范式。

第二范式2NF
若关系模式R∈1NF，并且每一个非主属性都完全函数依赖于任何一个候选码，则R∈2NF。

第三范式3NF
设关系模式R∈1NF,若R中不存在这样的码X、属性组Y及非主属性Z（Z ⊇ Y）, 使得X→Y，Y→Z成立，Y$\nrightarrow$X不成立，则称R ∈ 3NF。

BC范式BCNF
设关系模式R∈1NF，若X$\nrightarrow$Y且Y ⊆ X时X必含有码，则R∈BCNF。换言之，在关系模式R中，如果每一个决定属性集都包含候选码，则R∈BCNF。

多值依赖
设R(U)是属性集U上的一个关系模式。X,Y,Z是U的子集，并且Z=U-X-Y。关系模式R(U)中多值依赖X→→Y成立，当且仅当对R(U)的任一关系r，给定的一对(x,z)值，有一组Y的值，这组值仅仅决定于x值而与z值无关。

平凡多值依赖和非平凡的多值依赖：
若X→→Y，而Z＝Ф，则称X→→Y为平凡的多值依赖。否则称X→→Y为非平凡的多值依赖。

第四范式4NF
关系模式R∈1NF，如果对于R的每个非平凡多值依赖X→→Y（Y ⊈ X），X都含有码，则R∈4NF。

习题

1.建立一个关于系、学生、班级、学会等诸信息的关系数据库。
描述学生的属性有：学号、姓名、出生年月、系名、班号、宿合区，
描述班级的属性有：班号、专业名、系名、人数、入校年份；
描述系的属性有：系名、系号、系办公室地点、人数：
描述学会的属性有：学会名、成立年份、地点、人数。
有关语义如下：一个系有若干专业，每个专业每年只招一个班，每个班有若干学生。一个系的学生住在同一宿舍区。每个学生可参加若干学会，每个学会有若干学生。学生参加某学会有一个入会年份。
请给出关系模式， 指出是否存在传递函数依赖，对于函数依赖左部是多属性的情况，讨论函数依赖是完全函数依赖还是部分函数依赖。
指出各关系的候选码、外部码，并说明是否全码存在。

关系模式：
学生(学号,姓名,出生年月,系名,班号,宿合区)
S(SNO,SNAME,SDOB,DNAME,GNO,SLOC)
班级(班号,专业名,系名,人数,入校年份)
G(GNO,CNAME,DNAME,GNUM，GYEAR)
系(系名,系号,系办公室地点,人数)
D(DNAME,DNO,DADD,DNUM)
学会(学会名,成立年份,地点,人数)
P(PNAME,PYEAR,PADD,PNUM)
学生-学会(学号,学会名,入会年份)
S-P(SNO,PNAME,JYEAR)

传递函数依赖：
S：SNO→SNAME，S→SDOB， SNO→GNO， GNO→DNAME, DNAME→SLOC。
因为SNO→GNO， GNO→DNAME，所以存在传递函数依SNO→DNAME。
因为GNO→DNAME，DNAME→SLOC，所以存在传递函数依赖GNO→SLOC。
因为SNO→GNO，GNO→SLOC，所以存在传递函数依赖SNO→SLOC。

G：GNO→CNAME，GNO→GNUM，GNO→GYEAR，CNAME→DNAME，(GYEAR,CNAME)→GNO
因为GNO→CNAME，CNAME→DNAME，所以存在传递函数依赖GNO→DNAME。

D：DNO→DNAME，DNAME→DNO，DNO→DADD，DNO→DNUM
不存在传递函数依赖

P: PNAME→PYEAR，PNAME→PADD， PNAME→PNUM
不存在传递函数依赖

SP: (SNO，PNAME)→JYEAR
不存在传递函数依赖

完全函数依赖还是部分函数依赖：
(GYEAR,CNAME)→GNO, (SNO，PNAME)→JYEAR都是完全函数依赖

各关系的候选码、外部码，是否存在全码：

关系	候选码	外部码	是否存在全码
S	SNO	GNO,DNAME	否
G	GNO	DNAME	否
D	DNAME,DNO	无	否
P	PNAME	无	否
S-P	(SNO，PNAME)	SNO，PNAME	否

2.有关系模式 R(A，B，C，D，E)，回答下面各个问题：
（1）若A是R的候选码，具有函数依赖 BC→DE，那么在什么条件下R是BCNF?

BC也是R的候选码

（2）如果存在函数依赖A→B，BC→D，DE→A，列出R的所有码

BCE、ACE、CDE

（3）如果存在函数依赖A→B，BC→D，DE→A，R属于3NF还是BCNF.

R的候选码BCE、ACE、CDE，没有非主属性对码部分依赖或传递依赖，所R属于3NF。而三个函数依赖中，决定因素都不包含码，所以R不属于BCNF。

3.下面的结论哪些是正确的？哪些是错误的？对于错误的请给出一个反例说明之。
（1）任何一个二目关系是属于3NF的。

正确。只有两个属性不存在传递函数依赖。

（2）任何一个二目关系是属于BCNF的。

正确。只有两个属性，决定因素必含有码。

（3）任何一个二目关系是属于4NF的。

正确。只有两个属性不存在非平凡的多值依赖。

（4）当且仅当函数依赖A→B在R上成立，关系R(A，B，C）等于其投影R1（A，B）和R2（A，C）的连接。

错误。当函数依赖B→A在R上成立时，关系R(A，B，C）也等于其投影R1（A，B）和R2（A，C）的连接。

（5）若R.A→R.B，R.B→R.C则R.A→R.C。

正确。

（6）若R.A→R.B，R.A→R.C，则RA→R.(B，C）。

正确。

（7） 若R.B→R.A，R.C→R.A，则R.(B，C）→R.A。

正确。

（8）若R.(B，C)→R.A，则R.B→R.A，R.C→R.A。

错误。根据B、C两个属性才能确定A。例如知道学号和课程才能确定成绩，只知道学号或是只知道课程都不能确定成绩。

4.证明：
（1）如果R是BCNF关系模式，则R是3NF关系模式，反之则不然。

设R不是3NF.
则必然存在如下条件的函数依赖
X→Y（Y$\nrightarrow$X）,Y→Z
其中X是键属性,Y是任意属性组,Z是非主属性
Z属于Y,这样Y→Z函数依赖的决定因素Y不包含候选键,
与BCNF范式的定义相矛盾,
所以如果R属于BCNF,则R也是3NF.

（2）如果R是3NF关系模式，则R一定是2NF关系模式。

R(U,F)∈3NF
假设R中非主属性A部分依赖于关键字K
则存在K’是K的子集,使得F|=K’→A.
因K’是K的子集有K→K’,但K’$\nrightarrow$K.
于是有K→K’,K’$\nrightarrow$K,K’→A
并A不属于K,
因而A传递以来于K,即R不属于3NF,与已知矛盾.

这道证明题想了半天还是不会，就去网上搜了一下，但是因为好多给出的答案都是一样的，所以也不明白出处。

附加题

一．
Y(X1,X2,X3,X4)，(X1,X2)→X3，X2→X4
1.侯选码？
(X1,X2)
2.属于第几范式？
1NF。非主属性X4并不完全依赖于码，所以不属于2NF。

二．
R（A，B，C，D），F={AB→D，AC→BD，B→C}
1.侯选码？
AB,AC
2.最高属于第几范式？
3NF。决定属性B不包含候选码，非BCNF；无传递依赖，为3NF。

三．
R（X，Y，Z，W），F={Y←→W，XY→Z}
1.侯选码？
XY,XW
2.最高属于第几范式？
3NF。决定属性W、Y不包含候选码，非BCNF；无传递依赖，为3NF。

四.
R（A,B,C,D,E） F={A→B,CE→A,E→D}
1.求候选码。
CE
2.最高属于第几范式，为什么？
1NF。非主属性B、D并不完全依赖于码，非2NF。
3.分解到3NF。
R1（E，D），R2（A，B，C，E）

五.
R(商店编号，商品编号，数量，部门编号，负责人)
每个商店的每种商品只在一个部门销售，
每个商店的每个部门只有一个负责人，
每个商店的每种商品只有一个库存数量。
R(A,B,C,D,E),AB→C,AB→D,AD→E
1.求候选码。
AB
2.R已达第几范式？为什么？
2NF。每一个非主属性都完全函数依赖于任何一个候选码，存在传递依赖
3.若不属于3NF，分解成3NF。
R1(A,B,C,D),R2(A,D,E)

六．
R(A,B,C,D,E,F) F={A→C,AB→D,C→E,D→BF}
1.写出关键字。
候选码：AD,AB。1NF：非主属性E不完全函数依赖于任何一个候选码
2.分解到2NF。
R1(A,B,D,F),R2(A,C,E)
3.分解到3NF。
R1(A,B),R2(C,D,F,E)
4.分解到4NF。
R1(A,B),R2(C,E),R3(D,F)

总结：一共做了四个半小时，感觉判断候选码很熟练了，判断第几范式有时候记不清还得看下定义，不过还好，但是感觉多值依赖和第四范式有点难