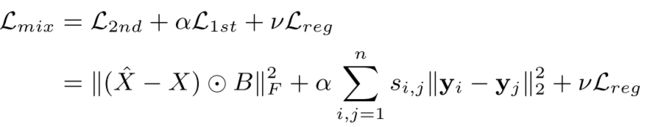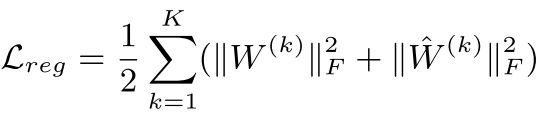论文分享 -- >Graph Embedding -- >Structural Deep Network Embedding

博客内容将首发在微信公众号"跟我一起读论文啦啦"，上面会定期分享机器学习、深度学习、数据挖掘、自然语言处理等高质量论文，欢迎关注！

本次要分享的论文是来自KDD2016的工作，论文链接Structural Deep Network Embedding，（简称SDNE）参考的代码链接 CODE。本篇论文第一次利用深度学习知识做图表示学习，其中也定义了与 LINE 中的一阶相似性和二阶相似性类似的概念，使其能够捕捉到图中高阶的非线性网络结构，同时能保留局部和全局结构信息，并且对稀疏网络具有较好的鲁棒性。与 LINE 论文方法相比，该论文方法在一些细节较容易让人理解。其实验部分证明了本方法与当时其他Graph Embedding方法相比，具有明显的优越性。

论文动机和创新点

• 现实世界中，图网络结构无处不在，例如在推荐系统，社群团体挖掘等应用上，如何挖掘图中的信息变得尤为重要。其中一个重要的基础问题就是，如何学习到有用的network embedding，通常的做法是将embedding空间映射到较低维的空间中进行节点的表示学习。

• network embedding的学习面临以下三个挑战：
  1、如何学习到图结构背后的高级非线性信息，是一个比较困难的事情。
  2、学习到的network embedding需要能保存 network structure信息，然而图的结构信息是非常复杂的，如何学习到节点的局部和全局结构信息是比较困难的。
  3、现实世界中，大部分图网络是稀疏的，如果仅仅利用由有边相连的部分进行学习，效果是很差的，所以学习到的network embedding能够对稀疏网络图具有鲁棒性。

• 上面提到的三个挑战，浅层模型很难有效解决，基于此，本文提出了 Structural Deep Network Embedding，即SDNE。更具体地说，
  1、利用深度神经网络，将数据映射到一个高度非线性的潜在空间以保存网络结构和捕捉高级的非线性特征信息，并且对稀疏网络具有鲁棒性。
  2、提出了一个新的半监督结构的深度模型，同时优化了一阶和二阶相似度，使得所学习的表示保留了局部和全局网络结构，并且对稀疏网络具有鲁棒性。

问题描述

图结构定义

$$G=(V,E)$$
上述公式中$V$ 表示 节点集合，$E$ 表示边集合，对每天边上的权重 $e=(u,v)\in E$, $s$ 为邻接矩阵；对于有权重图，$s_{i,j}$ 表示节点$i$ 和节点$j$ 的关系强弱；若无连接，则$s_{i,j}=0$，反之 $s_{i,j}>0$，若为无权重图，$s_{i,j}=1$。如上所描述的图G基本上可以囊括现实世界中的信息网络。

一阶相似度

对于图中任意两个节点$i,j$ 都可以由边进行连接，如果在图中两节点有边则 $s_{i,j}>0$，否则等于0，这种定义也是符合现实逻辑的，在information network中，如果两个用户存在连接关系，则该两个用户的性格、兴趣等可能存在相似性、如果两个网页存在连向彼此的链接，则该网页内容可能存在相似性等等。本文中一阶相似度用来保存全局图结构信息。

二阶相似度

显然一阶相似度有其局限性，仅仅利用了有边连接的部分进行学习，而现实世界中图大部分是稀疏的；二阶相似度指的是 图中两节点 相邻节点的相似程度。本文中二阶相似度用来保存局部图结构信息。

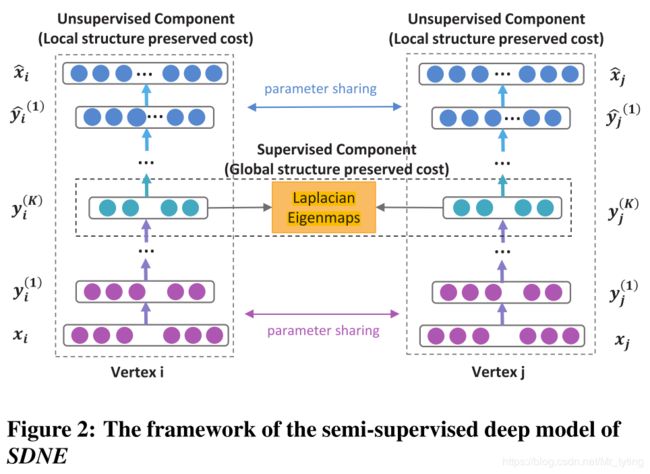
SDNE模型

损失函数

二阶相似度优化目标

可以查看上面SDNE网络图，图中深度自编码由多层神经网络组成:
$$y_i^{(1)}=\sigma (W^{(1)}{x}_i+b^{(1)})$$
$$y_i^{(k)}=\sigma (W^{(k)}{y}_i^{(k-1)}+b^{(k)}),k=2,3,4,...,K$$

其中，自编码输入为$x_i=s_i$，即为邻接矩阵的第$i$ 行数据。

自编码损失函数：

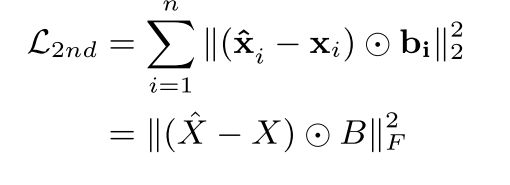
为了避免稀疏问题（$s_i$ 中可能存在大量0），这里加上一个惩罚项$B$ ，对非0元素给予更大的惩罚：
$$b_i=\{b_{i,j}{\}}_{j=1}^n$$
$$b_{i,j}=\{\begin{array}{cc}1& s_{i,j}=0\\ \beta >1& s_{i,j}>0\end{array}$$

显然以上这种重构过程，将使具有相似邻域结构的顶点具有相似的潜在表示，可以保存全局的网络结构信息。

一阶相似度优化目标

除了捕捉和保存图的全局结构信息，还需要捕捉保存图的局部结构信息。

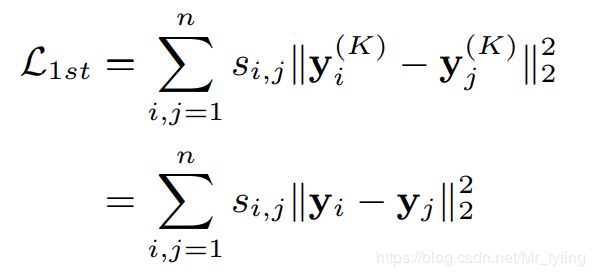
其中$s_{i,j}$ 表示节点$i$和节点$j$ 的权重，$y_i^{(k)}$ 表示节点$i$ 在自编码的第$k$ 层的降维输出，上式借鉴了 Laplacian Eigenmaps的思想，目的让相似的顶点在降维后的低维空间里仍旧尽量接近。

通过线性代数的知识，可将上式转化为如下：

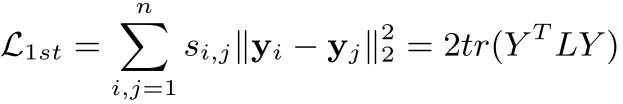
其中 $L=D-S$ 为图的拉普拉斯矩阵，D为图的度矩阵，S为邻接矩阵。

SDNE损失函数

其中：

整体算法流程

实验

本论文实验部分，利用了五个公开的数据集，在三类任务上进行了实验，与其baseline model相比，sdne方法无论在泛化能力上、对稀疏网络的鲁棒性上，可视化上等都有较大的优越性。

代码

代码参考自：keras-sdne

一阶、二阶损失函数

def l_2nd(beta):
    def loss_2nd(y_true, y_pred):
        b_ = np.ones_like(y_true)
        b_[y_true != 0] = beta
        x = K.square((y_true - y_pred) * b_)
        t = K.sum(x, axis=-1, )
        return K.mean(t)

    return loss_2nd


def l_1st(alpha):
    def loss_1st(y_true, y_pred):
        L = y_true
        Y = y_pred
        batch_size = tf.to_float(K.shape(L)[0])
        return alpha * 2 * tf.linalg.trace(tf.matmul(tf.matmul(Y, L, transpose_a=True), Y)) / batch_size

    return loss_1st

创建模型

def create_model(node_size, hidden_size=[256, 128], l1=1e-5, l2=1e-4):
    A = Input(shape=(node_size,))
    L = Input(shape=(None,))
    fc = A
    for i in range(len(hidden_size)):
        if i == len(hidden_size) - 1:
            fc = Dense(hidden_size[i], activation='relu',
                       kernel_regularizer=l1_l2(l1, l2), name='1st')(fc)
        else:
            fc = Dense(hidden_size[i], activation='relu',
                       kernel_regularizer=l1_l2(l1, l2))(fc)
    Y = fc
    for i in reversed(range(len(hidden_size) - 1)):
        fc = Dense(hidden_size[i], activation='relu',
                   kernel_regularizer=l1_l2(l1, l2))(fc)

    A_ = Dense(node_size, 'relu', name='2nd')(fc)
    ## A->A_ 自编码
   	## L->y  Laplacian Eigenmaps
    model = Model(inputs=[A, L], outputs=[A_, Y]) 
    emb = Model(inputs=A, outputs=Y)
    return model, emb

模型训练

 def train(self, batch_size=1024, epochs=1, initial_epoch=0, verbose=1):
        if batch_size >= self.node_size:
            if batch_size > self.node_size:
                print('batch_size({0}) > node_size({1}),set batch_size = {1}'.format(
                    batch_size, self.node_size))
                batch_size = self.node_size
            return self.model.fit([self.A.todense(), self.L.todense()], [self.A.todense(), self.L.todense()],
                                  batch_size=batch_size, epochs=epochs, initial_epoch=initial_epoch, verbose=verbose,
                                  shuffle=False, )
        else:
            steps_per_epoch = (self.node_size - 1) // batch_size + 1
            hist = History()
            hist.on_train_begin()
            logs = {}
            for epoch in range(initial_epoch, epochs):
                start_time = time.time()
                losses = np.zeros(3)
                for i in range(steps_per_epoch):
                    index = np.arange(
                        i * batch_size, min((i + 1) * batch_size, self.node_size))
                    A_train = self.A[index, :].todense()
                    L_mat_train = self.L[index][:, index].todense()
                    inp = [A_train, L_mat_train]
                    ## inp 作为模型的输入；同时又做模型的y_true
                    batch_losses = self.model.train_on_batch(inp, inp)
                    losses += batch_losses
                losses = losses / steps_per_epoch

个人总结

• 本论文方法中的 一阶二阶相似度的计算方式，比起LINE来说，直观上较好理解。